Area Of Equilateral Triangle

The area of an equilateral triangle is the amount of space that it occupies in a 2-dimensional plane. To recall, an equilateral triangle is a triangle in which all the sides are equal and the measure of all the internal angles is 60°. So, an equilateral triangle’s area can be calculated if the length of its side is known.

Area of an Equilateral Triangle Formula

The formula for the area of an equilateral triangle is given as:

Where a = length of sides

Learn more about isosceles triangles, equilateral triangles and scalene triangles here.

Derivation for Area of Equilateral Triangle

There are three methods to derive the formula for the area of equilateral triangles. They are:

• Using basic triangle formula
• Using rectangle construction
• Using trigonometry

Deriving Area of Equilateral Triangle Using Basic Triangle Formula

Take an equilateral triangle of the side “a” units. Then draw a perpendicular bisector to the base of height “h”.

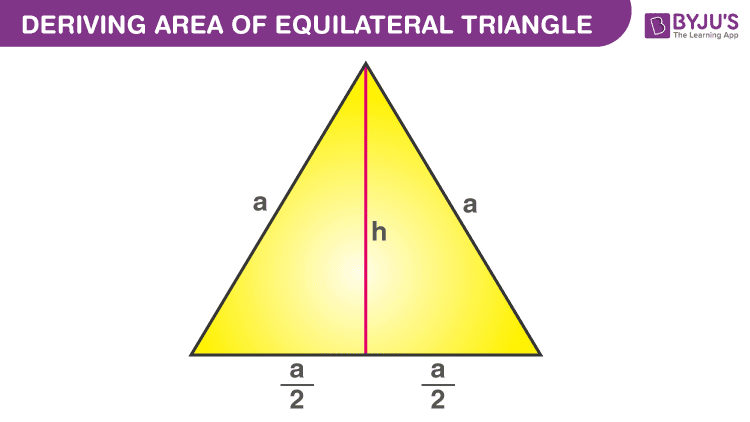
Deriving Area Of Equilateral Triangle

Now,

Area of Triangle = ½ × base × height

Here, base = a, and height = h

Now, apply Pythagoras Theorem in the triangle.

a² = h² + (a/2)²

⇒ h² = a² – (a²/4)

⇒ h² = (3a²)/4

Or, h = ½(√3a)

Now, put the value of “h” in the area of the triangle equation.

Area of Triangle = ½ × base × height

⇒ A = ½ × a × ½(√3a)

Or, Area of Equilateral Triangle = ¼(√3a²)

Deriving Area of Equilateral Triangle Using Rectangle Construction

Consider an equilateral triangle having sides equal to “a”.

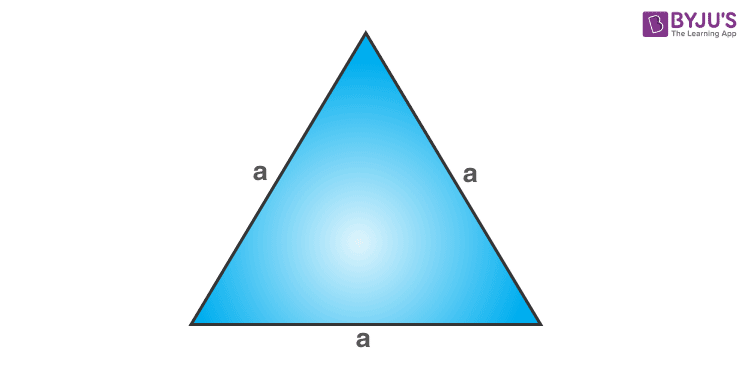
Equilateral Triangle

• Now, draw a straight line from the top vertex of the triangle to the midpoint of the base of the triangle, thus, dividing the base into two equal halves.

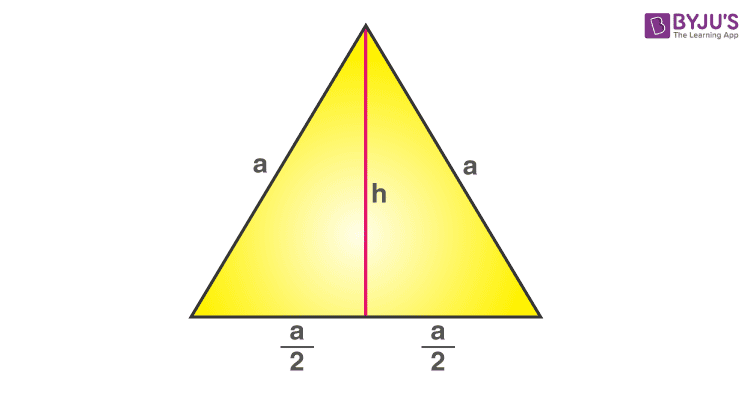
Area Of Equilateral Triangle

• Now cut along the straight line and move the other half of the triangle to form the rectangle.

How to find Area of Equilateral Triangle?

Here, the length of the equilateral triangle is considered to be ‘a’ and the height as ‘h’

So the area of an equilateral triangle = Area of a rectangle = ½×a×h …………. (i)

Half of the rectangle is a right-angled triangle as it can be seen from the figure above.

Thereby, applying the Pythagoras Theorem:

⇒ a² = h² +  (a/2)²

⇒ h² = (3/4)a²

⇒ h = (√3/2)a ……………(ii)

Substituting the value of (ii) in (i), we have:

Area of an Equilateral Triangle

=(½)×a×(√3/2)a

=(√3/4)a²

Deriving Area of Equilateral Triangle Using Trigonometry

If two sides of a triangle are given, then the height can be calculated using trigonometric functions. Now, the height of a triangle ABC will be-

h = b. Sin C = c. Sin A = a. Sin B

Now, area of ABC = ½ × a × (b . sin C) = ½ × b × (c . sin A) = ½ × c (a . sin B)

Now, since it is an equilateral triangle, A = B = C = 60°

And a = b = c

Area = ½ × a × (a . Sin 60°) = ½ × a² × Sin 60° = ½ × a² × √3/2

So, Area of Equilateral Triangle = (√3/4)a²

Below is a brief recall about equilateral triangles:

What is an Equilateral Triangle?

There are mainly three types of triangles which are scalene triangles, equilateral triangles and isosceles triangles. An equilateral triangle has all the three sides equal and all angles equal to 60°. All the angles in an equilateral triangle are congruent.

Properties of Equilateral Triangle

An equilateral triangle is the one in which all three sides are equal. It is a special case of the isosceles triangle where the third side is also equal. In an equilateral triangle ABC, AB = BC = CA.

Some important properties of an equilateral triangle are:

• An equilateral triangle is a triangle in which all three sides are equal.
• Equilateral triangles also called equiangular. That means, all three internal angles are equal to each other and the only value possible is 60° each.
• It is a regular polygon with 3 sides.
• A triangle is equilateral if and only if the circumcenters of any three of the smaller triangles have the same distance from the centroid.
• A triangle is equilateral if and only if any three of the smaller triangles have either the same perimeter or the same inradius.
• The area of an equilateral triangle is basically the amount of space occupied by an equilateral triangle.
• In an equilateral triangle, the median, angle bisector and perpendicular are all the same and can be simply termed as the perpendicular bisector due to congruence conditions.
• The ortho-centre and centroid of the triangle is the same point.
• In an equilateral triangle, median, angle bisector and altitude for all sides are all the same and are the lines of symmetry of the equilateral triangle.
• The area of an equilateral triangle is √3 a²/ 4
• The perimeter of an equilateral triangle is 3a.

Example Questions Using the Equilateral Triangle Area Formula

Question 1: Find the area of an equilateral triangle whose perimeter is 12 cm.

Solution:

Given: Perimeter of an equilateral triangle = 12 cm

As per formula: Perimeter of the equilateral triangle = 3a, where “a” is the side of the equilateral triangle.

Step 1: Find the side of an equilateral triangle using perimeter.

3a = 12

a = 4

Thus, the length of side is 4 cm.

Step 2: Find the area of an equilateral triangle using formula.

Area, A = √3 a²/ 4 sq units

= √3 (4)²/ 4 cm²

= 4√3 cm²

Therefore, the area of the given equilateral triangle is 4√3 cm²

Question 2: What is the area of an equilateral triangle whose side is 8 cm?

Solution:

The area of the equilateral triangle = √3 a²/ 4

= √3 × (8²)/ 4 cm²

= √3 × 16 cm²

= 16 √3 cm²

Question 3: Find the area of an equilateral triangle whose side is 7 cm.

Solution:

Given,

Side of the equilateral triangle = a = 7 cm

Area of an equilateral triangle = √3 a²/ 4

= (√3/4) × 7² cm²

= (√3/4) × 49 cm²

= 21.21762 cm²

Question 4: Find the area of an equilateral triangle whose side is 28 cm.

Solution:

Given,

Side of the equilateral triangle (a) = 28 cm

We know,

Area of an equilateral triangle = √3 a²/ 4

= (√3/4) × 28² cm²

= (√3/4) × 784 cm²

= 339.48196 cm²