There are basically six different types of triangles with respect to the length and measure of the lines and angles of a triangle, respectively. To recall, a triangle is a specific type of polygon having only three sides and three angles. Based on these specifications and design, the properties of triangles are defined for all its different types.
As the name suggests, a “triangle” is a three-sided polygon having three angles. The sum of all interior angles of a triangle will always add up to 180 degrees. This is called the angle sum property of triangle. Also, a triangle has many properties. Let us discuss in detail about the triangle types.
Also check: Mathematics for Grade 10, to learn more about triangles.
| Table of contents: |
Six Types of Triangles
Triangles can be broadly classified into two types, which are:
- Triangles based on the lengths of their sides
- Triangles based on their interior angles
These two triangle types are explained here along with their further classifications.
| Based on their Sides | Based on their Angles |
|---|---|
| Scalene Triangle | Acute Triangle |
| Isosceles Triangle | Obtuse Triangle |
| Equilateral Triangle | Right Triangle |
We will discuss all the above triangles broadly in the next section to differentiate among them all. Also, will see the properties of each triangle related to them.
Also, read:
Types of Triangles Based on Sides
According to the lengths of their sides, triangles can be classified into three types which are:
- Scalene
- Isosceles
- Equilateral
Let us discuss them one by one.
Scalene Triangle
A scalene triangle has all side lengths of different measures. No side will be equal in length to any of the other sides in such a triangle. In a scalene triangle, all the interior angles are also different. The figure given below illustrates a scalene triangle. You can see how none of the sides is equal in length.

In the above-given figure, you can see that all the sides of the triangle seem to be unequal.
Isosceles Triangle
In an isosceles triangle, the lengths of two of the three sides are equal. So, the angles opposite the equal sides are equal to each other. In other words, an isosceles triangle has two equal sides and two equal angles. The figure given below illustrates an isosceles triangle.

In the above figure, we can see the two sides of the triangle appears to be equal, whereas the base of the triangle here is smaller than the other two sides.
Equilateral Triangle
In an equilateral triangle, all the lengths of the sides are equal. In such a case, each of the interior angles will have a measure of 60 degrees. Since the angles of an equilateral triangle are same, it is also known as an equiangular triangle. The figure given below illustrates an equilateral triangle.

In the above figure, all the three sides of the triangles are equal as well as all the interior angles equal to 60 degrees.
Types of Triangles Based on Angles
Triangles can be classified into three types with respect to their interior angles which are:
- Acute-angled
- Obtuse-angled
- Right-angled
Acute Triangle
An acute triangle is a triangle whose all the three interior angles are acute. In other words, if all interior angles are less than 90 degrees, then it is an acute-angled triangle. The figure given below illustrates an acute triangle.
In the above figure, we can see all the interior angles of the triangle, is less than 90 degrees, hence it is an acute triangle.
Obtuse Triangle
Obtuse triangles are those in which one of the three interior angles has a measure greater than 90 degrees. In other words, if one of the angles in a triangle is an obtuse angle, then the triangle is called an obtuse-angled triangle. The figure given below illustrates an obtuse triangle.
In the above triangle, we can see that one of the angles is more than 90 degrees. Hence, it is an obtuse triangle.
Right Triangle
A right triangle is a triangle in which one of the angles is 90 degrees. In a right-angled triangle, the side opposite to the right angle (90-degree angle) will be the longest side and is called the hypotenuse. You may come across triangle types with combined names like right isosceles triangle and such, but this only implies that the triangle has two equal sides with one of the interior angles being 90 degrees. The figure given below illustrates a right triangle.
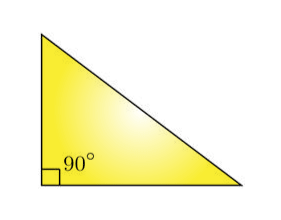
In the above triangle, one among the three angles is 90 degrees, thus it is a right triangle.
Video Lesson on Types of Triangles
Geometry is all about shapes like square, circle, rectangle, triangle and so on. Among all the shapes that we have listed here, triangles seem to be fun and different. Triangle is a shape that is made up of three lines and three angles. Watch this video to know how the triangle is different from other shapes and see how you can learn and remember different types of triangles easily from the video.
We see triangles everywhere. If we somehow manage to bring three lines together, we can see a triangle is formed. There are different types of triangles – equilateral triangles, isosceles triangles, scalene triangles and so on. The names of these triangles don’t even sound English.
Do you know how these triangles got these names? Watch this video to know the trivia behind triangles and learn its properties in the simplest way.

Frequently Asked Questions on Types of Triangles
Write down the types of triangles classified based on its sides.
Based on the sides of a triangle, a triangle is classified into three different types, namely:
Scalene Triangle
Isosceles Triangle
Equilateral Triangle
Mention the classification of a triangle based on its angle.
Based on the angles of a triangle, a triangle is classified as:
Acute Triangle
Right Triangle
Obtuse Triangle
Define scalene, isosceles and equilateral triangle.
In a scalene triangle, all the sides of a triangle are of different length. In an isosceles triangle, two sides of a triangle are of the same measure. In an equilateral triangle, all the sides of a triangle are of equal length.
Define acute, obtuse and right triangle.
In an acute triangle, all the angles of a triangle are less than 90 degrees.
In an obtuse triangle, one of the angles of a triangle is greater than 90 degrees.
In a right triangle, one angle measures 90 degrees and the other two angles are acute.
Can an acute triangle be a scalene triangle?
An acute triangle can be a scalene triangle, isosceles triangle or equilateral triangle. The acute triangle can be drawn if the triangle has equal or unequal side lengths.
To learn more about such maths topics in an easy and effective way, download BYJU’S – The Learning App. Register to get engaging and interactive video lessons and take free tests to practise for exams.




Very good app. I could complete my project with ease . Thanks to the founder of this app
It also helps me with my homework.
Very good app for the students and also elders who want to learn the basics.
Thank you byjus i could complete my project.