Right Angled Triangle

A right-angled triangle is a triangle, that has one of its interior angles equal to 90 degrees or any one angle is a right angle. Therefore, this triangle is also called the right triangle or 90-degree triangle. The right triangle plays an important role in trigonometry. Let us learn more about this triangle in this article. 

What is a Triangle?

A triangle is a regular polygon, with three sides and the sum of any two sides is always greater than the third side. This is a unique property of a triangle. In other words, it can be said that any closed figure with three sides and the sum of all the three internal angles is equal to 180°.

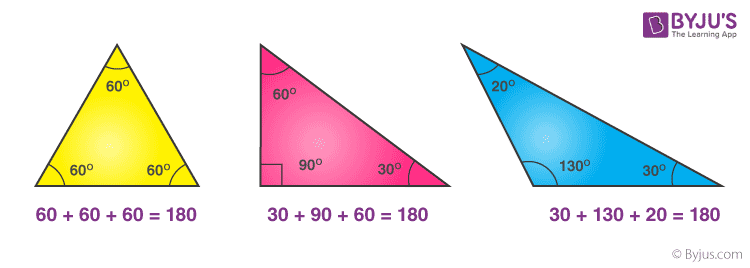
Being a closed figure, a triangle can have different types and each shape is described by the angle made by any two adjacent sides.

Types of Triangles

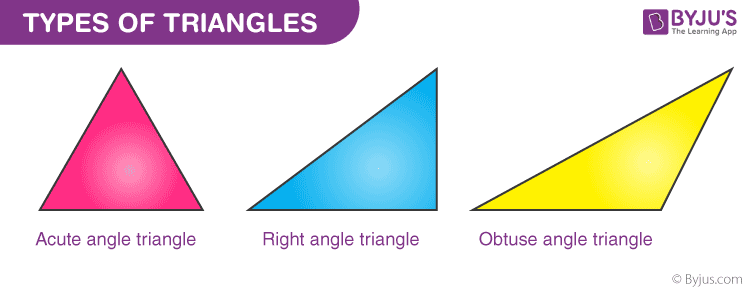
1. Acute angle triangle: When the angle between any 2 sides is less than 90 degrees it is called an acute angle triangle.
2. Right angle triangle: When the angle between a pair of sides is equal to 90 degrees it is called a right-angle triangle.
3. Obtuse angle triangle: When the angle between a pair of sides is greater than 90 degrees it is called an obtuse angle triangle.

The other three types of triangles are based on the sides of the triangle. 

• Scalene triangle (All the three sides are unequal)
• Isosceles triangle (Two sides are equal)
• Equilateral triangle (All the three sides are equal)

Note: A scalene triangle and an isosceles triangle both can be a right triangle. A scalene right triangle will have all three sides unequal in length and any of the one angles will be a right angle. An isosceles right triangle will have its base and perpendicular sides equal in length, which includes the right angle. The third unequal side will be the hypotenuse.

Watch The Below Video To Learn More About the Types of Triangles

Right Angled Triangle

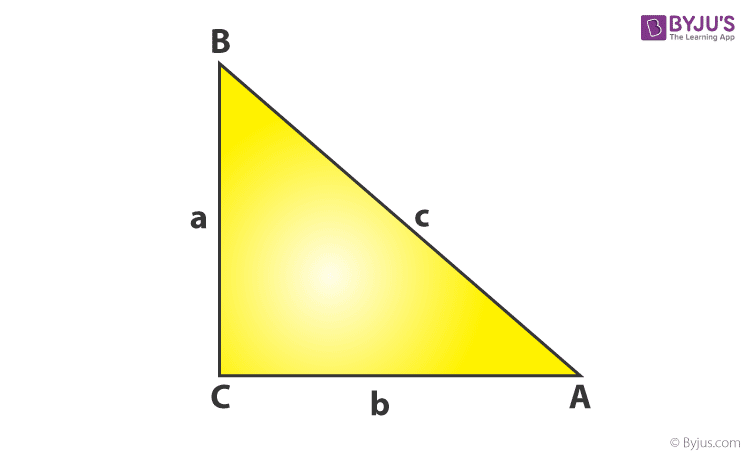
A right-angled triangle is a type of triangle that has one of its angles equal to 90 degrees. The other two angles sum up to 90 degrees. The sides that include the right angle are perpendicular and the base of the triangle. The third side is called the hypotenuse, which is the longest side of all three sides. 

The three sides of the right triangle are related to each other. This relationship is explained by Pythagoras theorem. According to this theorem, in a right triangle,

Hypotenuse² = Perpendicular² + Base²

See the figure below to understand better.

The area of the biggest square is equal to the sum of the square of the two other small square areas. We can generate the Pythagoras theorem as the square of the length of the hypotenuse is equal to the sum of the length of squares of base and height.

Shape of Right Triangle

A right triangle is a three-sided closed shape, that has one perpendicular side called the leg or height of the triangle. 

Right Angle Triangle Properties

Let us discuss, the properties carried by a right-angle triangle.

• One angle is always 90° or right angle.
• The side opposite angle of 90° is the hypotenuse.
• The hypotenuse is always the longest side.
• The sum of the other two interior angles is equal to 90°.
• The other two sides adjacent to the right angle are called base and perpendicular.
• The area of the right-angle triangle is equal to half of the product of adjacent sides of the right angle, i.e.,

                            Area of Right Angle Triangle = ½ (Base × Perpendicular)

• If we drop a perpendicular from the right angle to the hypotenuse, we will get three similar triangles.
• If we draw a circumcircle that passes through all three vertices, then the radius of this circle is equal to half of the length of the hypotenuse.
• If one of the angles is 90° and the other two angles are equal to 45° each, then the triangle is called an Isosceles Right Angled Triangle, where the adjacent sides to 90° are equal in length.

Above were the general properties of the Right angle triangle. The construction of the right angle triangle is also very easy. Keep learning with BYJU’S to get more such study materials related to different topics of Geometry and other subjective topics.

Area of Right Angled Triangle

The area is in the two-dimensional region and is measured in a square unit. It can be defined as the amount of space taken by the 2-dimensional object.

The area of a triangle can be calculated by 2 formulas:

And, Heron’s formula

Here, s is the semi perimeter and is calculated as:

Where, a, b, c are the sides of a triangle.

Let us calculate the area of a triangle using the figure given below.

Fig 1: Let us drop a perpendicular to the base b in the given triangle.

Fig 2: Now let us attach another triangle to a side of the triangle. It forms the shape of a parallelogram as shown in the figure.

Fig 3: Let us move the red coloured triangle to the other side of the parallelogram as shown in the above figure.

Fig 4: It takes up the shape of a rectangle now.

Now by the property of area, it is calculated as the multiplication of any two sides

Hence, area =b × h (for a rectangle)

Therefore, the area of a right angle triangle will be half i.e.

For a right-angled triangle, the base is always perpendicular to the height. When the sides of the triangle are not given and only angles are given, the area of a right-angled triangle can be calculated by the given formula:

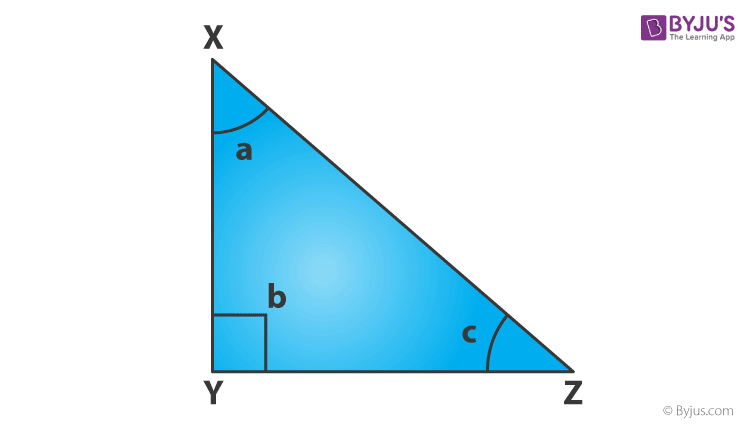
Where a, b, c are respective angles of the right-angle triangle, with ∠b always being 90°.

Perimeter

As we know, the three sides of the right triangle are Base, Perpendicular and Hypotenuse. Thus the perimeter of the right triangle is the sum of all its three sides.

Perimeter of right triangle = Length of (Base + Perpendicular + Hypotenuse)

Example: If Base =4cm, Perpendicular= 3cm and Hypotenuse = 5cm. What is the perimeter of right triangle?

Perimeter = 4 + 3 + 5 = 12 cm

Solved Examples

Q.1: In a right triangle, if perpendicular = 8 cm and base = 6 cm, then what is the value of hypotenuse?

Solution: Given,

Perpendicular = 8 cm

Base = 6cm

We need to find the hypotenuse.

By Pythagoras theorem, we know that;

Hypotenuse = √(Perpendicular² + Base²)

H = √(6² + 8²)

= √36 + 64

= √100

= 10 cm

Therefore, the hypotenuse of the right triangle is 10 cm.

Q.2: If the hypotenuse is 13 cm and the base is 12 cm, then find the length of perpendicular of the right triangle?

Solution: Given,

Hypotenuse = 13 cm

Base = 12 cm

Perpendicular = ?

By Pythagoras theorem, we know that,

Hypotenuse² = Perpendicular² + Base²

Perpendicular² = Hypotenuse² – Base²

P = √(13² – 12²)

P = √(169 – 144)

P = √25

P = 5 cm

Therefore, the value of perpendicular is 5cm.

Practice Problems

1. Find the perpendicular length if a right triangle has a base of 2 units and a hypotenuse of √8 units.
2. What is the area of the right triangle with a base of 7 cm and a hypotenuse of 25 cm?
3. Show that in a right-angled triangle, the hypotenuse is the longest side.

To learn more interesting facts about triangles stay tuned with BYJU’S.