Differentiation and Integration are the two major concepts of calculus. Differentiation is used to study the small change of a quantity with respect to unit change of another. (Check the Differentiation Rules here). On the other hand, integration is used to add small and discrete data, which cannot be added singularly and representing in a single value. The real-life example of differentiation is the rate of change of speed with respect to time (i.e.velocity) and for integration, the greatest example is to find the area between the curve for large scale industries.
What is Differentiation?
Differentiation is the essence of Calculus. A derivative is defined as the instantaneous rate of change in function based on one of its variables. It is similar to finding the slope of a tangent to the function at a point.
Suppose you need to find the slope of the tangent line to a graph at point P. The slope can be approximated by drawing a line through point P and finding the slope by a line that is known as the secant line.
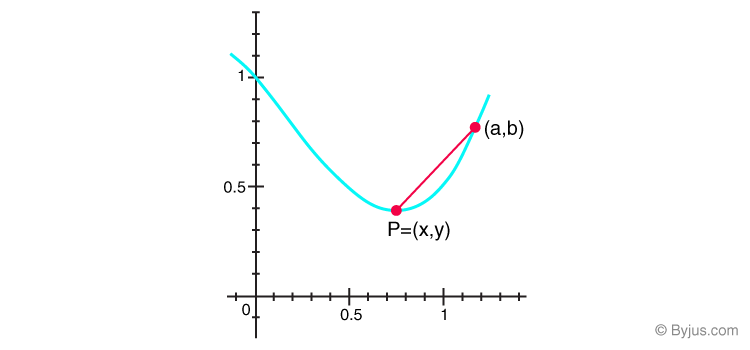
A function f in x is said to be differentiable at the point x = a, if the derivative f'(a) exists at every point in its domain. The derivative of a function f(x) is given by:

For a function to be differentiable at any point x = a, in its domain, it must be continuous at that particular point but vice-versa is necessarily not always true. The domain of f’(x) is defined by the existence of its limits.
If y = f(x) is a function in x, then the derivative of f(x) is given as dy/dx. This is known as the derivative of y with respect to x.
Also, the derivative of a function f(x) at x = a, is given by:

The derivative of a function f(x) signifies the rate of change of the function f(x) with respect to x at a point ‘a’, lying in its domain.
Learn in detail: Differentiation
If the derivative of the function, f’, is known which is differentiable in its domain then we can find the function f. In integral calculus, we call f as the anti-derivative or primitive of the function f’. The method of calculating the anti-derivative is known as anti-differentiation or integration.
What is integration?
Integration is a method to find definite and indefinite integrals. The integration of a function f(x) is given by F(x) and it is represented by:
![]()
where
R.H.S. of the equation indicates integral of f(x) with respect to x
F(x) is called anti-derivative or primitive.
f(x) is called the integrand.
dx is called the integrating agent.
C is the constant of integration or arbitrary constant.
x is the variable of integration.
This integral is called indefinite integral, because the limits are not defined here.
Now for a function f(x) and any closed interval say [a,b], the definite integral is given by:
∫ab f(x) dx
From the above discussion, it can be said that differentiation and integration are the reverse processes of each other.
Learn more: Integration
Differentiation and Integration Formulas
Let us discuss here the general formulas used in integration and differentiation.
| Differentiation Formulas | Integration Formulas |
| d/dx (a) = 0 where a is constant | ∫ 1 dx = x+C |
| d/dx (x) = 1 | ∫ a dx = ax + C |
| d/dx(xn) = nxn-1 | ∫ xn dx = (xn+1/n+1) + C |
| d/dx sin x = cos x | ∫ sin x dx = -cos x + C |
| d/dx cos x = -sin x | ∫ cos x dx = sin x + C |
| d/dx tan x = sec2 x | ∫ sec2 x dx = tan x + C |
| d/dx ln x = 1/x | ∫ (1/x) dx = ln x + C |
| d/dx ex = ex | ∫ ex dx = ex + C |
Also check:
Properties of Differentiation and Integration
Let us now compare differentiation and integration based on their properties:
- Differentiation and integration both satisfy the property of linearity, i.e.,k1 and k2 are constants in the above equations.
- Differentiation and Integration, both operations involve limits for their determination.
- Both differentiation and integration, as discussed are inverse processes of each other.
- The derivative of any function is unique but on the other hand, the integral of every function is not unique. Two integrals of the same function may differ by a constant.
- Upon differentiating a polynomial function the degree of the result is 1 less than the degree of the polynomial function whereas in case of integration the result obtained has a degree which is 1 greater than the degree of the polynomial function.
- While dealing with derivatives we can consider derivative at a point whereas, in the integrals, integral of a function over an interval is considered.
- Geometrically, the derivative of a function describes the rate of change of a quantity with respect to another quantity while indefinite integral represents the family of curves positioned parallel to each other having parallel tangents at the intersection point of every curve of the family with the lines orthogonal to the axis representing the variable of integration.
To learn more about differentiation and integration, you can visit us at BYJU’S or download the app to get interactive videos.

How can deal with geometric progression
Need more basics as a beginner.
TYPE BYJUS . COM AND DO /MATHS/DIFFRENTIATION
SEE HERE YOU WILL GET ALL
I WOULD GIVE YOU DIRECT LINK BUT HERE IT IS NOT ALLOWING SO PLEASE TRY YOURSELF REMOVING SPACES