Integration

Integration is the calculation of an integral. Integrals in maths are used to find many useful quantities such as areas, volumes, displacement, etc. When we speak about integrals, it is related to usually definite integrals. The indefinite integrals are used for antiderivatives. Integration is one of the two major calculus topics in Mathematics, apart from differentiation(which measure the rate of change of any function with respect to its variables). It’s a vast topic which is discussed at higher level classes like in Class 11 and 12. Integration by parts and by the substitution is explained broadly. Here, you will learn the definition of integrals in Maths, formulas of integration along with examples.

Table of Contents:

• Integration Definition
• Integral Calculus
• Integration – Inverse Process of Differentiation
• Integrals
  • Definite Integral
  • Indefinite Integral
• Integration Formulas
• Examples
• FAQs

Integration Definition

The integration denotes the summation of discrete data. The integral is calculated to find the functions which will describe the area, displacement, volume, that occurs due to a collection of small data, which cannot be measured singularly. In a broad sense, in calculus, the idea of limit is used where algebra and geometry are implemented. Limits help us in the study of the result of points on a graph such as how they get closer to each other until their distance is almost zero. We know that there are two major types of calculus –

• Differential Calculus
• Integral Calculus

The concept of integration has developed to solve the following types of problems:

• To find the problem function, when its derivatives are given.
• To find the area bounded by the graph of a function under certain constraints.

These two problems lead to the development of the concept called the “Integral Calculus”, which consist of definite and indefinite integral. In calculus, the concept of differentiating a function and integrating a function is linked using the theorem called the Fundamental Theorem of Calculus. 

Maths Integration

In Maths, integration is a method of adding or summing up the parts to find the whole. It is a reverse process of differentiation, where we reduce the functions into parts. This method is used to find the summation under a vast scale. Calculation of small addition problems is an easy task which we can do manually or by using calculators as well. But for big addition problems, where the limits could reach to even infinity, integration methods are used. Integration and differentiation both are important parts of calculus. The concept level of these topics is very high. Hence, it is introduced to us at higher secondary classes and then in engineering or higher education. To get an in-depth knowledge of integrals, read the complete article here.

Integral Calculus

According to Mathematician Bernhard Riemann,

“Integral is based on a limiting procedure which approximates the area of a curvilinear region by breaking the region into thin vertical slabs.” Learn more about Integral calculus here.

Let us now try to understand what does that mean:

• Take an example of a slope of a line in a graph to see what differential calculus is:

In general, we can find the slope by using the slope formula. But what if we are given to find an area of a curve? For a curve, the slope of the points varies, and it is then we need differential calculus to find the slope of a curve.

You must be familiar with finding out the derivative of a function using the rules of the derivative. Wasn’t it interesting? Now you are going to learn the other way round to find the original function using the rules in Integrating.

Integration – Inverse Process of Differentiation

We know that differentiation is the process of finding the derivative of the functions and integration is the process of finding the antiderivative of a function. So, these processes are inverse of each other. So we can say that integration is the inverse process of differentiation or vice versa. The integration is also called the anti-differentiation. In this process, we are provided with the derivative of a function and asked to find out the function (i.e., primitive). 

We know that the differentiation of sin x is cos x. 

It is mathematically written as:

(d/dx) sinx = cos x …(1)

Here, cos x is the derivative of sin x. So, sin x is the antiderivative of the function cos x. Also, any real number “C” is considered as a constant function and the derivative of the constant function is zero. 

So, equation (1) can be written as

(d/dx) (sinx + C)= cos x +0

(d/dx) (sinx + C)= cos x 

Where “C” is the arbitrary constant or constant of integration.

Generally, we can write the function as follow:

(d/dx) [F(x)+C] = f(x), where x belongs to the interval I.

To represent the antiderivative of “f”, the integral symbol “∫” symbol is introduced. The antiderivative of the function is represented as ∫ f(x) dx. This can also be read as the indefinite integral of the function “f” with respect to x.

Therefore, the symbolic representation of the antiderivative of a function (Integration) is:

y = ∫ f(x) dx

∫ f(x) dx = F(x) + C.

Integrals in Maths

You have learned until now the concept of integration. You will come across, two types of integrals in maths:

• Definite Integral

• Indefinite Integral

Definite Integral

An integral that contains the upper and lower limits then it is a definite integral. On a real line, x is restricted to lie. Riemann Integral is the other name of the Definite Integral.

A definite Integral is represented as:

Indefinite Integral

Indefinite integrals are defined without upper and lower limits. It is represented as:

∫f(x)dx = F(x) + C

Where C is any constant and the function f(x) is called the integrand.

Integration Formulas

Check below the formulas of integral or integration, which are commonly used in higher-level maths calculations. Using these formulas, you can easily solve any problems related to integration.

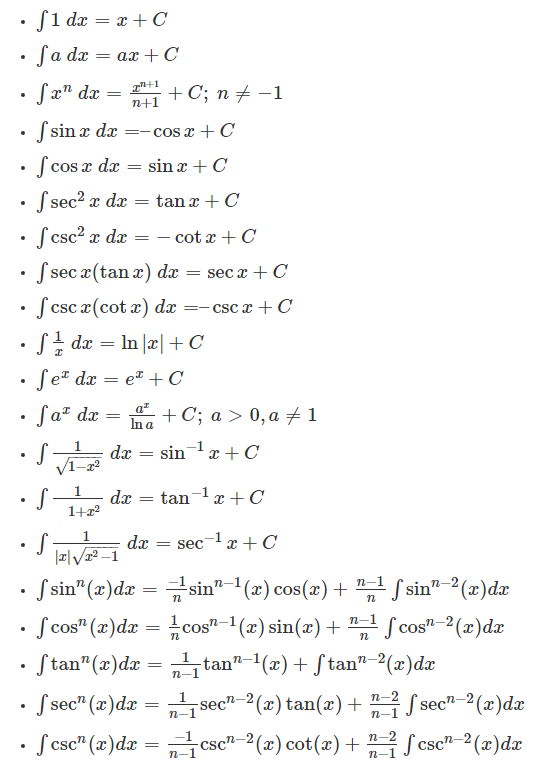
Also, get some more complete definite integral formulas here.

Integration Examples

Solve some problems based on integration concept and formulas here.

Example 1: Find the integral of the function:

Solution:

= 9

Example 2: Find the integral of the function: ∫x² dx

Solution:

Given ∫x² dx

= (x³/3) + C.

Example 3:

Integrate ∫ (x²-1)(4+3x)dx.

Solution:

Given: ∫ (x²-1)(4+3x)dx.

Multiply the terms, we get

∫ (x²-1)(4+3x)dx = ∫ 4x²+3x³-3x-4 dx

Now, integrate it, we get

∫ (x²-1)(4+3x)dx  = 4(x³/3) + 3(x⁴/4)- 3(x²/2) – 4x + C

The antiderivative of the given function ∫  (x²-1)(4+3x)dx is 4(x³/3) + 3(x⁴/4)- 3(x²/2) – 4x + C.

Video Lesson on Class 12 Important Calculus Questions

Download BYJU’S – The Learning App to get personalised videos for all the important Maths topics. Also, learn about differentiation-integration concepts briefly here.