In Maths or in Geometry, a Cube is a solid three-dimensional figure, which has 6 square faces, 8 vertices and 12 edges. It is also said to be a regular hexahedron. You must have seen 3 × 3 Rubik’s cube, which is the most common example in the real-life and it is helpful to enhance brain power. In the same way, you will come across many real-life examples, such as 6 sided dice, etc. Solid geometry is all about three-dimensional shapes and figures, which have surface areas and volumes. The other solid shapes are cuboid, cylinder, cone, sphere. We will discuss here its definition, properties and its importance in Maths. Also, learn the surface area formula for the cube along with its volume formula.
Table of contents:
- Definition
- Shape
- Area and Volume
- Properties
- Difference Between Square and Cube
- How to make Cube
- Examples
- Practice Problems
- FAQs
Cube Definition
As discussed earlier, a cube is a 3-D
solid shape, which has 6 faces. A cube is one of the simplest shapes in three-dimensional space. All the six faces of a cube are squares, a two-dimensional shape.
Cube Shape
Sometimes, the shape of a cube is considered as “cubic”. We can also say that a cube is considered as a block, where all the length, breadth and height are the same. Along with that, it has 8 vertices and 12 edges such that 3 edges meet at one vertex point. Check the given image below, defining its faces, edges and vertices. It is also known as a square parallelepiped, an equilateral cuboid and a right rhombohedron. The cube is one of the platonic solids and it is considered as the convex polyhedron where all the faces are square. We can say that the cube has octahedral or cubical symmetry. A cube is the special case of the square prism.
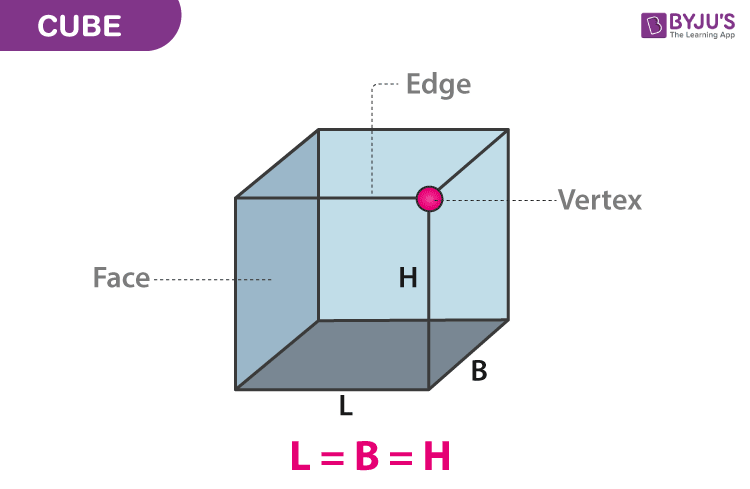
In the above figure, you can see, edge, face and vertex of the cube. Here, L stands for length, B stands for breadth and H stands for height. We can see the length, breadth and height of the cube, which represents the edges of the cube, connected at a single point which is the vertex. The faces of the cube are connected by four vertices. Since the cube is a 3D shape, the two important parameters used to measure the cube are surface area and volume. Now let us discuss the properties of the cube along with the formula for surface area and volume.
Surface Area and Volume Formula For Cube
The surface area and the volume of the cube are discussed below:
Surface Area of a Cube
We know that for any shape, the area is defined as the region occupied by it in a plane. A cube is a three-dimensional object, therefore, the area occupied by it will be in a 3d plane. Since a cube has six faces, therefore, we need to calculate the surface area of the cube, covered by each face. The formula to find the surface area can be found as given below.
Let a be the edge of the cube.
Area of one face = Area of a square = a2
We know that the cube has 6 square shaped faces.
Lateral surface area (excluding the top and bottom faces) = 4 × Area of one face
LSA = 4a2
Total surface area = LSA + Area of the top and bottom faces
TSA = 4a2 + a2 + a2
TSA = 6a2
|
Volume of Cube
The volume of the cube is the space contained in it. Suppose, if an object is in cubical shape and we need to immerse any material in it, say water, then the measure of water in litres to be kept in the object is calculated by its volume. The formula of the volume is given by:
|
For More Information On Volumes of Cubes and Cuboid, Watch The Below Video:

Length of Diagonal of Cube
If a is the length of the side, then,
- Length of Diagonal of Face of the Cube = √2 a
- Length of Diagonal of Cube = √3 a
Also, see:
Properties of Cube
The following are the important properties of cube:
- It has all its faces in a square shape.
- All the faces or sides have equal dimensions.
- The plane angles of the cube are the right angle.
- Each of the faces meets the other four faces.
- Each of the vertices meets the three faces and three edges.
- The edges opposite to each other are parallel.
Difference Between Square and Cube
The major difference between the square and the cube is the square is a two-dimensional figure and it has only two dimensions such as length and breadth, whereas the cube is a three-dimensional figure and its three dimensions are length, breadth and height. The cube is obtained from the shape square.
How to Make a Cube Shape?
A cube can be formed by folding a net of six squares connected each other as shown in figure given below:

Cube Examples
Example 1:
If the value of the side of the cube is 10 cm, then find its surface area and volume.
Solution:
Given, side, a = 10 cm
Therefore, by the surface area and volume formula of the cube, we can write;
Surface Area = 6a2 = 6 × 102 = 6 × 100.= 600 cm2
Volume = a3 = 103 = 1000 cm3
Example 2:
Find the side length of a cube whose volume is 512 cm3.
Solution:
Given: Volume of cube, v = 512 cm2
We know that the formula for the volume of a cube is a3 cubic units.
Therefore, 512 = a3
512 can be written as 83
83 = a3
Therefore, a= 8
Hence, the side length of the cube, a = 8 cm.
Practice Problems
Solve the following problems given below:
- The side length of the cube is 6 cm. Find its surface area.
- Determine the volume of a cube whose side length is 4 cm.
- Find the volume of the cube whose surface area is 24 cm2.
- Find the diagonal length of the cube when a = 9 cm.
Frequently Asked Questions on Cube
What is a cube?
A cube is a three-dimensional figure with 6 faces, 8 vertices and 12 edges. A cube is just a special case of prism.
What is the difference between cube and cuboid?
A cube is a three-dimensional form of square and all the faces of a cube are square. Whereas, a cuboid is a three-dimensional form of rectangle and all the faces are rectangles.
Write down the formula to calculate the surface area of a cube.
The formula to calculate the surface area of a cube is 6a2 square units, where “a” is the side length of a cube.
How to calculate the volume of a cube?
Since all the sides of a cube are equal, the volume of a cube is calculated as a3 cubic units, where “a” is the side length.
Can we say a cube is a prism?
A cube is still a prism, because a cube is considered as one of the Platonic solids.
Learn more about different geometrical shapes and figures here at BYJU’S. Also, download its app to get a visual of such figures and understand the concepts in a better way.


It’s very useful for everyone. Thank you
Thank for mathmetic properties help and I memerized deeply
I want 10 examples of cube, can anyone please tell me?
It is avery use ful
well defined and easy to learn
Hello
This will help me in my holiday homework