A cuboid is a three-dimensional figure bounded by six rectangular planes, having a different magnitude of length, width and height. If you look around and you can see a box, brick or anything in the shape of a rectangle, it could be cuboid. A cuboid (3-dimensional) can be seen made up of rectangles (2-dimensional) of different dimensions when seen from any of the ends. In this article, we are going to discuss the definition of cuboid, total and lateral surface area of a cuboid in a detailed way.
Table of Contents:
- Cuboid Definition
- Surface Area of Cuboid Formula
- Total Surface Area of a Cuboid Derivation
- Examples
- FAQs
Cuboid Definition
A cuboid is a three-dimensional figure or solid which has six rectangular sides called faces. Each face of a cuboid is a rectangle and all of its corners are 90-degrees. It has 8 vertices and 12 edges. The opposite faces of a cuboid are always equal. It means that the opposite surfaces of the cuboid are in the same dimension. The measures of the cuboid are the Total Surface Area (TSA), Lateral or curved Surface Area (CSA) and volume. The surface areas are measured in terms of square units, whereas the volume of the cube is measured in terms of cubic units.
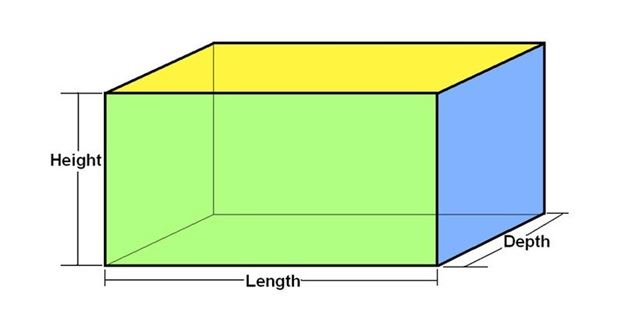
Area of Cuboid
The area of a cuboid refers to the surface area as the cuboid is a three dimensional solid. Thus, the area of cuboid can be calculated using the formula of area of rectangle, since the faces of a cuboid are in a rectangular shape.
Cuboid Surface Area
The surface area of the cuboid can be of two types-
(i) Total Surface Area
(ii) Lateral Surface Area or Curved Surface Area
Surface Area of Cuboid Formula
Before going into the concept of area, let us denote the dimensions of a cuboid, which are,
Length, Width, and Height are represented by l, w, h, respectively.
Total Surface Area of a Cuboid
The Total surface area of a cuboid (TSA) is equal to the sum of the areas of it’s 6 rectangular faces, which is given by:
Total Surface Area of a Cuboid (TSA) = 2 (lw + wh + lh) square units
The above formula gives the total surface area of a cuboid having all six faces.
Lateral Surface Area of a Cuboid
The lateral surface area of a cuboid is the sum of 4 planes of a rectangle, leaving the top (upper) and the base (lower) surface. Mathematically, the Lateral Surface Area of a cuboid (LSA) is given as:
Lateral Surface Area of a cuboid (LSA) = 2 (lh + wh) = 2 h (l + w) square units
Also, learn:
- Cuboid and Cube
- Volume of a Cuboid
- Surface area and Volumes
- 3D shapes
- Difference Between Cube and Cuboid
Total Surface Area of a Cuboid Derivation
As the cuboid has six rectangular faces, the total surface area of the cuboid is calculated as follows:
Assume that, l, w, h be the length, width, and height of the cuboid respectively.
Thus,
The front face area of cuboid = l x h
The back face area of the cuboid = l x h
The top face area of the cuboid = l x w
The bottom face area of the cuboid = l x w
The left face area of the cuboid = h x w
The right face area of cuboid = h x w
Hence, the total surface area is the sum of all the faces of a cuboid, then the TSA of a cuboid is:
Total Surface Area of Cuboid = lh + lh + lw+ lw+ hw+ hw
Total Surface Area of Cuboid = 2 lh + 2 lw + 2 hw
Total Surface Area of Cuboid = 2 (lh + lw+ hw)
Therefore, the total surface area of the cuboid is 2 (lh + lw+ hw) square units.
Surface Area of Cuboid Example
Example 1:
Given below is a cuboid having its dimension given as length = 8 cm, width = 6 cm and height = 5 cm, find the TSA of a cuboid.
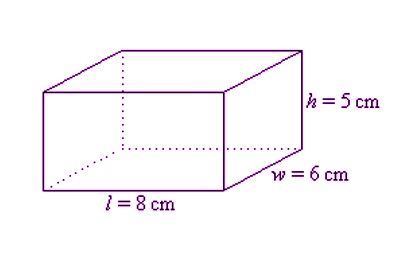
Solution
Given:
h = 5 cm
w = 6 cm
l = 8 cm
Using the formula: TSA = 2 (lw + wh + hl)
2( (8×6) + (6×5) + (5×8))
= 2(48 + 30 + 40)
= 2(118)
= 236
So, the total surface area of this cuboid is 236 cm².
Example 2:
The dimensions of a cuboid are given as follows:
Length = 4.8 cm
Width = 3.4 cm
Height = 7.2 cm.
Find the Total Surface area and the Lateral Surface area.
Solution:
The total surface area is given as
TSA = 2 (lw + wh + hl)
=2((4.8 ×3.4) + (3.4×7.2) + (7.2×4.8))
= 2(16.32 +24.48 +34.56)
= 2(75.36) cm²
Therefore, TSA of a cuboid= 150.72 cm
Also, the lateral surface area = 2 h (l + w)
= 2×7.2 (4.8 + 3.4)
= 14.4 (8.2) = 118.08
Therefore, LSA of a cuboid = 118.08 cm²
Learn more about various geometrical figures, surface areas and volumes by visiting our site BYJU’S – The Learning App.
Frequently Asked Questions on Surface Area of Cuboid
What is the surface area of the cube and cuboid?
LSA = 4a^2
TSA = 6a^2
The surface area of the cuboid can be found using the formulas given below:
LSA = 2h(l + b)
TSA = 2(lb + bh + hl)
What is the latest surface area of a cuboid?
LSA = 2h(l + b)
How do you find the surface area and volume of a cuboid?
Surface area of cuboid = 2(lb + bh + hl)
The volume of the cuboid is calculated using the formula:
Volume = lbh


Awesome explanation.
Satisfied with answer.