Triangles

In Geometry, a triangle is a three-sided polygon that consists of three edges and three vertices. The most important property of a triangle is that the sum of the internal angles of a triangle is equal to 180 degrees. This property is called angle sum property of triangle. 

If ABC is a triangle, then it is denoted as ∆ABC, where A, B and C are the vertices of the triangle. A triangle is a two-dimensional shape, in Euclidean geometry, which is seen as three non-collinear points in a unique plane. 

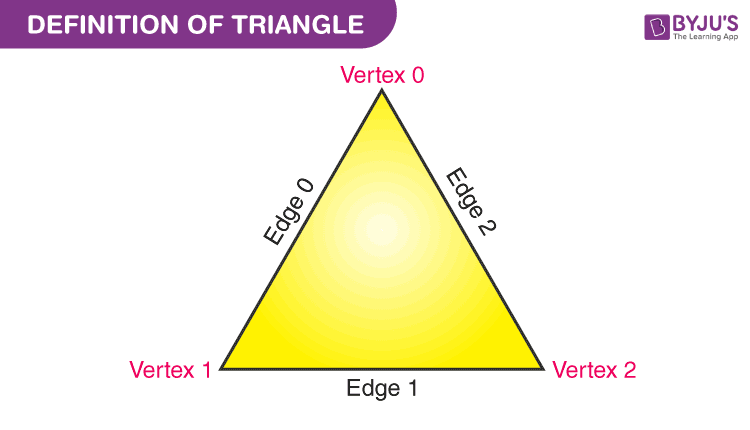
Below given is a triangle having three sides and three edges, which are numbered as 0,1,2.

Definition

As we discussed in the introduction, a triangle is a type of polygon, which has three sides, and the two sides are joined end to end is called the vertex of the triangle. An angle is formed between two sides. This is one of the important parts of geometry. 

Some major concepts, such as Pythagoras theorem and trigonometry, are dependent on triangle properties. A triangle has different types based on its angles and sides. 

Shape of Triangle

Triangle is a closed two-dimensional shape. It is a three-sided polygon. All sides are made of straight lines. The point where two straight lines join is the vertex. Hence, the triangle has three vertices. Each vertex forms an angle.

Angles of Triangle

There are three angles in a triangle. These angles are formed by two sides of the triangle, which meets at a common point, known as the vertex. The sum of all three interior angles is equal to 180 degrees. 

If we extend the side length outwards, then it forms an exterior angle. The sum of consecutive interior and exterior angles of a triangle is supplementary. 

Let us say, ∠1, ∠2 and ∠3 are the interior angles of a triangle. When we extend the sides of the triangle in the outward direction, then the three exterior angles formed are ∠4, ∠5 and ∠6, which are consecutive to ∠1, ∠2 and ∠3, respectively.

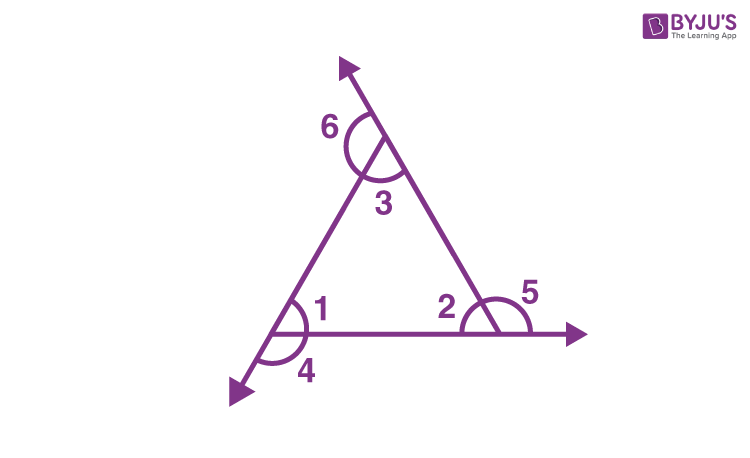
Hence, 

∠1 + ∠4 = 180°   ……(i)

∠2 + ∠5 = 180°  …..(ii)

∠3 + ∠6 = 180°  …..(iii)

If we add the above three equations, we get;

∠1+∠2+∠3+∠4+∠5+∠6 = 180° + 180° + 180°

Now, by angle sum property we know, 

∠1+∠2+∠3 = 180°

Therefore, 

180 + ∠4+∠5+∠6 = 180° + 180° + 180°

∠4+∠5+∠6 = 360°

This proves that the sum of the exterior angles of a triangle is equal to 360 degrees.

Properties

Each and every shape in Maths has some properties which distinguish them from each other. Let us discuss here some of the properties of triangles.

1. A triangle has three sides and three angles.
2. The sum of the angles of a triangle is always 180 degrees.
3. The exterior angles of a triangle always add up to 360 degrees.
4. The sum of consecutive interior and exterior angle is supplementary.
5. The sum of the lengths of any two sides of a triangle is greater than the length of the third side. Similarly, the difference between the lengths of any two sides of a triangle is less than the length of the third side.
6. The shortest side is always opposite the smallest interior angle. Similarly, the longest side is always opposite the largest interior angle.

Also, read:

Types

On the basis of length of the sides, triangles are classified into three categories:

1. Scalene Triangle
2. Isosceles Triangle
3. Equilateral Triangle

On the basis of measurement of the angles, triangles are classified into three categories:

1. Acute Angle Triangle
2. Right Angle Triangle
3. Obtuse Angle Triangle

Scalene Triangle

A scalene triangle is a type of triangle, in which all the three sides have different side measures. Due to this, the three angles are also different from each other.

Isosceles Triangle

In an isosceles triangle, two sides have equal length. The two angles opposite to the two equal sides are also equal to each other.

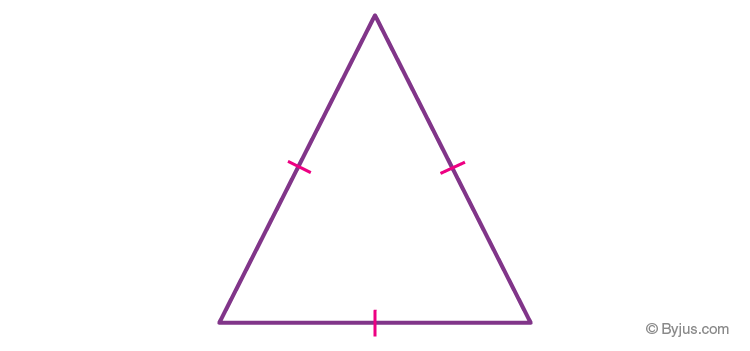
Equilateral Triangle

An equilateral triangle has all three sides equal to each other. Due to this all the internal angles are of equal degrees, i.e. each of the angles is 60°

Acute Angled Triangle

An acute triangle has all of its angles less than 90°.

Right Angled Triangle

In a right triangle, one of the angles is equal to 90° or right angle.

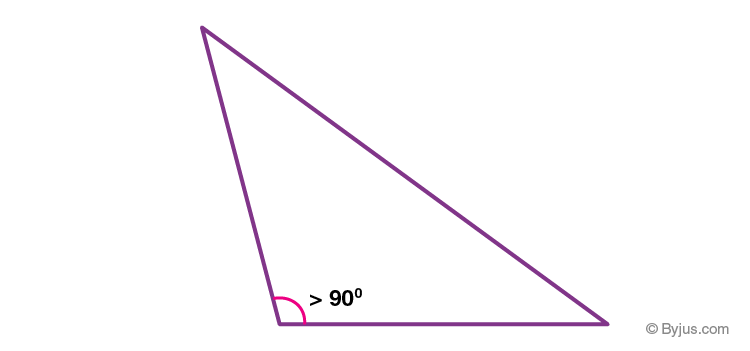
Obtuse Angled Triangle

An obtuse triangle has any of its one angles more than 90°.

Perimeter of Triangle

A perimeter of a triangle is defined as the total length of the outer boundary of the triangle. Or we can say, the perimeter of the triangle is equal to the sum of all its three sides. The unit of the perimeter is same as the unit of sides of the triangle. 

If ABC is a triangle, where AB, BC and AC are the lengths of its sides, then the perimeter of ABC is given by:

Perimeter = AB+BC+AC

Area of a Triangle

The area of a triangle is the region occupied by the triangle in 2d space. The area for different triangles varies from each other depending on their dimensions. We can calculate the area if we know the base length and the height of a triangle. It is measured in square units.

Suppose a triangle with base ‘B’ and height ‘H’ is given to us, then, the area of a triangle is given by-

Area of Triangle Using Heron’s Formula

In case, if the height of a triangle is not given, we cannot be able to use the above formula to find the area of a triangle.

Therefore, Heron’s formula is used to calculate the area of a triangle, if all the sides lengths are known.

First, we need to calculate the semi perimeter (s).

s = (a+b+c)/2,                     (where a,b,c are the three sides of a triangle)

Now Area is given by; A = √[s(s-a)(s-b)(s-c)]

Solved Examples

Question 1: If ABC is a triangle where AB = 3cm, BC=5cm and AC = 4cm, then find its perimeter.

Solution: Given, ABC is a triangle.

AB = 3cm

BC = 5cm

AC = 4cm

As we know by the formula, 

Perimeter = Sum of all three sides

P = AB + BC + AC

P = 3+5+4

P = 12cm

Triangles: Introduction