A triangle is a three-sided polygon. It has three sides and three angles. The three sides and three angles share an important relationship. In Mathematics, the term “inequality” represents the meaning “not equal”. Let us consider a simple example if the expressions in the equations are not equal, we can say it as inequality. In this article, let us discuss what is triangle inequality in Maths, activities for explaining the concept of the triangle inequality theorem, and so on.
| Also, read: |
What is Triangle Inequality?
In Mathematics, the term “triangle inequality” is meant for any triangles. Let us take a, b, and c are the lengths of the three sides of a triangle, in which no side is being greater than the side c, then the triangle inequality states that,
c ≤ a+b
This states that the sum of any two sides of a triangle is greater than or equal to the third side of a triangle.
Activity For Triangle Inequality Theorem
Let us discuss the relationship and equality and inequality of triangle, through an activity.
Activity 1: On a paper mark two points Y and Z and join them to form a straight line. Mark another point X outside the line lying on the same plane of the paper. Join XY as shown.
Now mark another point X’ on the line segment XY, join X’Z. Similarly, mark X’’ and join X’’Z with dotted lines as shown.
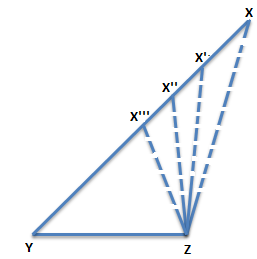
From the above figure we can easily deduce that if we keep on decreasing the length of side XY such that XY> X’Y> X’’Y> X’’’Y the angle opposite to side XY also decreases i.e. ∠XZY >∠X’ZY >∠X’’ZY >∠X’’’ZY. Thus, from the above activity, we can infer that if we keep on increasing one side of a triangle then the angle opposite to it increases.
Now let us try out another activity.
Activity: Draw 3 scalene triangles on a sheet of paper as shown.
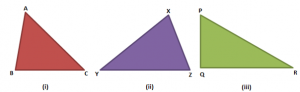
Let us consider fig. (i). In ∆ABC, AC is the longest side and AB is the shortest. We observe that ∠B is the largest in measure and ∠C is the smallest. Similarly, in ∆XYZ, XY is the largest side and XZ is the smallest and ∠Z is the largest in measure and ∠Y is the smallest. In the last figure also the same kind of pattern is followed i.e. side PR is largest and so is the ∠Q opposite to it.
Triangle Inequality Theorem
Let us consider the triangle. The following are the triangle inequality theorems.
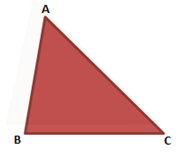
Theorem 1: In a triangle, the side opposite to the largest side is greatest in measure.
The converse of the above theorem is also true according to which in a triangle the side opposite to a greater angle is the longest side of the triangle.
In the above fig., since AC is the longest side, the largest angle in the triangle is ∠B.
Another theorem which follows can be stated as:
Theorem 2: The sum of lengths of any two sides of a triangle is greater than the length of its third side.
According to triangle inequality, AB + BC > AC.
Video Lesson on BPT and Similar Triangles

To learn more about triangle inequality proof and other properties please download BYJU’S- The Learning App.


Comments