What is Binary Division?
The binary division operation is similar to the base 10 decimal system, except the base 2. The division is probably one of the most challenging operations of the basic arithmetic operations. There are different ways to solve division problems using binary operations. Long division is one of them and the easiest and the most efficient way. This section has been designed to answer questions about binary division, including:
- What is Binary division?
- Procedure to add two binary numbers
- Examples to Solve Binary division
Binary Division Rules
The binary division is much easier than the decimal division when you remember the following division rules. The main rules of the binary division include:
- 1÷1 = 1
- 1÷0 = Meaningless
- 0÷1 = 0
- 0÷0 = Meaningless
Similar to the decimal number system, the binary division is similar, which follows the four-step process:
- Divide
- Multiply
- Subtract
- Bring down
Important Note: Binary division follows the long division method to find the resultant in an easy way.
Comparison with Decimal Value
(01111100)2 = (1111100)2 = 12410
(0010)2 = (10)2 = 210
You will get the resultant value as 62 when you divide 124 by 2.
So the binary equivalent of 62 is (111110)2
(111110)2 = 6210
Both the binary and the decimal system produce the same result.
Binary Division Examples
Example 1.
Question: Solve 01111100 ÷ 0010
Solution:
Given
01111100 ÷ 0010
Here the dividend is 01111100, and the divisor is 0010
Remove the zero’s in the Most Significant Bit in both the dividend and divisor, that doesn’t change the value of the number.
So the dividend becomes 1111100, and the divisor becomes 10.
Now, use the long division method.

- Step 1: First, look at the first two numbers in the dividend and compare with the divisor. Add the number 1 in the quotient place. Then subtract the value, you get 1 as remainder.
- Step 2: Then bring down the next number from the dividend portion and do the step 1 process again
- Step 3: Repeat the process until the remainder becomes zero by comparing the dividend and the divisor value.
- Step 4: Now, in this case, after you get the remainder value as 0, you have zero left in the dividend portion, so bring that zero to the quotient portion.
Therefore, the resultant value is quotient value which is equal to 111110
So, 01111100 ÷ 0010 = 111110
Example 2: Solve using the long division method: 101101 ÷ 101
Solution:
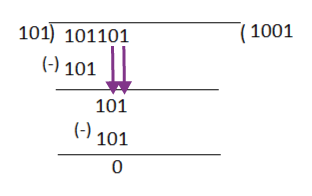
So, when you bring down the fourth bit of the dividend, it does not match with the divisor. In order to bring down the 5th and 6th bit of the dividend, add two zeros in the quotient value.
For more such examples on binary operations like addition, subtraction, multiplication and division operations register with BYJU’S -The Learning App and also watch exciting videos to learn with ease.
| More Topics Related to Binary Division | |
|---|---|
| Binary Multiplication | Binary Calculator |
| Binary Addition | Binary Subtraction |
Frequently Asked Questions
What is Binary Division?
In Binary division, two binary numbers of base 2 can be divided using the basic binary division rules.
What are the Rules of Binary Division?
The rules of binary division are:
- 1÷1 = 1
- 1÷0 = Meaningless
- 0÷1 = 0
- 0÷0 = Meaningless


why cant u explain for engineering students also
not only me many of engineering students will be happy with it
Thanks my problem are solved