You are already aware of the term ‘triangle’ and its properties. Before exploring more about them, let us go through some of their basic properties. A triangle is a three-sided polygon which has 3 vertices and 3 sides enclosing 3 angles. Based on the length of its sides, a triangle can be classified into scalene, isosceles and equilateral. Based on the measure of its angles, it can be an acute-angled, obtuse-angled or right-angled triangle. The sum of interior angles in a triangle is 180 degrees. In this article, we introduce you to two more terms- altitude and median of the triangle.
Median of a Triangle

Properties of Median of a Triangle

- Every triangle has 3 medians, one from each vertex. AE, BF and CD are the 3 medians of the triangle ABC.
- The 3 medians always meet at a single point, no matter what the shape of the triangle is.
- The point where the 3 medians meet is called the centroid of the triangle. Point O is the centroid of the triangle ABC.
- Each median of a triangle divides the triangle into two smaller triangles which have equal area.
- In fact, the 3 medians divide the triangle into 6 smaller triangles of equal area.
Altitude of Triangle
An altitude of a triangle is a line segment that starts from the vertex and meets the opposite side at right angles.
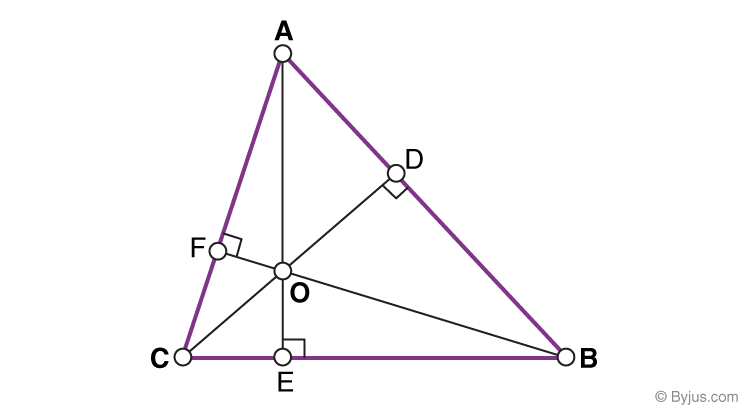
Properties of Altitudes of a Triangle
- Every triangle has 3 altitudes, one from each vertex. AE, BF and CD are the 3 altitudes of the triangle ABC.
- The altitude is the shortest distance from the vertex to its opposite side.
- The 3 altitudes always meet at a single point, no matter what the shape of the triangle is.
- The point where the 3 altitudes meet is called the ortho-centre of the triangle. Point O is the ortho-centre of the triangle ABC.
- The altitude of a triangle may lie inside or outside the triangle.
To learn more about the altitude and median of a triangle, download BYJU’S – The Learning App.


Best app for study material and project notes