Mean Deviation For Continuous Frequency Distribution

Class Registration Banner

Data representation in a tabular or graphical form indicates the frequency (number of times an observation occurs within a particular interval) is known as a frequency distribution.

If the data is huge, for example, if we need to analyze the marks of 200 students, then the representation of such data in a random fashion is not very practical. So, we use the concept of ‘Grouping of Data’ based on class intervals. In the upcoming discussion, we will discuss how to calculate the mean deviation for the continuous frequency distribution of data.

Mean Deviation - For Grouped Data Continuous Frequency Distribution

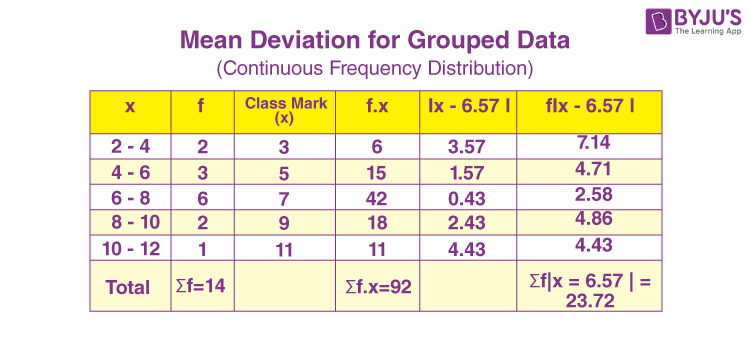
Mean Deviation of Grouped Data

In frequency distribution of continuous type, the class intervals or groups are arranged so that there are no gaps between the classes and each class in the table has its respective frequency. The class intervals are chosen in such a way that they must be mutually exclusive and exhaustive.

To understand the concept of continuous frequency distribution, let us take the following example:

The following table represents the age group of employees working in a certain company.

Age Group Number of people
15-25 25
25-35 54
35-45 34
45-55 20

This representation is continuous in nature, and the frequency is mentioned according to the class interval.

Steps to Calculate Mean Deviation of Continuous Frequency Distribution

To calculate the mean deviation for continuous frequency distribution, the following steps are followed:

Step i) Assume that the frequency in each class is centered at the mid-point. The mean is calculated for these mid-points.

Considering the above example, the midpoints are given as follows:

Age Group
\(\begin{array}{l}x_i\end{array} \)
 Number of people
\(\begin{array}{l}(f_i)\end{array} \)
15-25 20 25
25-35 30 54
35-45 40 34
45-55 50 20

The mean is calculated by the formula

\(\begin{array}{l}\overline{x} = \frac{1}{N}\sum\limits_{i=1}^{n}x_if_i\end{array} \)

Step ii) The mean absolute deviation about the mean is given by:

\(\begin{array}{l}M.A.D.(\overline{x})= \frac{1}{N}\sum\limits_{i=1}^{n}f_i|x_i – \overline{x}|\end{array} \)

The above example can be tabulated as:

Age Group
\(\begin{array}{l}x_i\end{array} \)
 Number of people
\(\begin{array}{l}f_i\end{array} \)
\(\begin{array}{l}f_ix_i\end{array} \)
\(\begin{array}{l}|x_i~-~\overline{x}|\end{array} \)
\(\begin{array}{l}f_i|x_i~-~\overline{x}|\end{array} \)
15-25 20 25 500 13.684 324.1
25-35 30 54 1620 3.684 198.936
35-45 40 34 1360 6.316 214.744
45-55 50 20 1000 16.316 326.32
\(\begin{array}{l}\sum~f_i = 133\end{array} \)
\(\begin{array}{l}\overline{x}=\frac{1}{N}\sum\limits_{i=1}^{n}~x_if_i=33.684\end{array} \)
\(\begin{array}{l}\sum\limits_{i=1}^{n}f_i|x_i~-~\overline{x}| = 1064.1\end{array} \)

Now

\(\begin{array}{l}M.A.D.(\overline{x}) = \frac{1}{N}\sum\limits_{i=1}^{n}f_i|x_i~-~\overline{x}| = \frac{1064.1}{133} = 8.00 (approximately)\end{array} \)

Note: Sometimes, the mean is calculated using the Step Deviation Method to reduce the complexity. The observation which lies in the middle or close to the mid-value is considered the assumed mean. The result obtained is more or less the same. This method reduces the size of the observations and, therefore, calculation complexity reduces.

The formula used is:

\(\begin{array}{l}M.A.D.(\overline{x}) = a + \frac{h}{N}\sum\limits_{i=1}^{n} ~f_i d_i\end{array} \)

Where “a” is the assumed mean, “h” is the common factor and

\(\begin{array}{l}d = \frac{x_i~-~a}{h}\end{array} \)

Similarly, to calculate the mean deviation about the median we need to find out the median of the given set of data with the help of cumulative frequency, which is given as-

\(\begin{array}{l}M = l+\frac{\frac{N}{2}-C}{f}\times h\end{array} \)

Where, “l” is the lower limit of the median class,

“f” is the frequency of median class,

“h” is the width of class and,

“C” is the cumulative frequency of the preceding class.

The median class has a cumulative frequency of just greater than N/2.

We find the mean deviation about the median using the formula:

\(\begin{array}{l}M.A.D (M) = \frac{1}{N} \sum_{i=1}^{n}f_{i}|x_{i}-M|\end{array} \)

In the example given, the mean deviation about the median is given as follows:

Class Frequency Cumulative Frequency Mid-Point
\(\begin{array}{l}|x_i~-~M|\end{array} \)
\(\begin{array}{l}f_i|x_i~-~M|\end{array} \)
5-15 5 5 10 17.857 89.285
15-25 9 14 20 7.857 70.713
25-35 7 21 30 2.143 15.001
35-45 3 24 40 12.143 36.429
45-55 8 32 50 22.143 177.144
32 388.572

Here,  N/2 = 16.  Therefore the class 25 – 35 is the median class.

\(\begin{array}{l}M = l+\frac{\frac{N}{2}-C}{f}\times h\end{array} \)
\(\begin{array}{l}M = 25 + \frac{16 – 14}{7}\times 10\end{array} \)
\(\begin{array}{l}M = 27.857\end{array} \)

The mean deviation about the median is

\(\begin{array}{l}M.A.D (M) = \frac{1}{N} \sum_{i=1}^{n}f_{i}|x_{i}-M|\end{array} \)
\(\begin{array}{l}M.A.D (M) = \frac{388.572}{32}\end{array} \)
\(\begin{array}{l}M.A.D (M) = 12.14\end{array} \)

This is the method used to find the mean deviation of grouped data. Please log on to www.byjus.com to know more.


MATHS Related Links
Class 12 Maths Index Exponential Distribution
Bayes Theorem Example Cross Product Of Two Vectors
Multiplication Tricks Precision
Linear Differential Equation T Distribution
Surface Area Of Rectangle Regular Hexagon

Comments

Leave a Comment

Your Mobile number and Email id will not be published.

*

*

  1.  alex mpande
    November 4, 2020 at 6:14 pm

    nice i have got it

    Reply