Most of the phenomena studied in the domain of Engineering and Science are periodic in nature. For instance, current and voltage in an alternating current circuit. These periodic functions could be analyzed into their constituent components (fundamentals and harmonics) by a process called Fourier analysis.
Table of Contents:
Periodic functions occur frequently in the problems studied during Engineering education. Their representation in terms of simple periodic functions such as sine and cosine function, which leads to Fourier series(FS). Fourier series is a very powerful tool in connection with various problems involving partial differential equations. In this article, let us discuss the Fourier analysis with examples.
Also, read:
What is the Fourier Series?
A Fourier series is an expansion of a periodic function f(x) in terms of an infinite sum of sines and cosines. Fourier Series makes use of the orthogonality relationships of the sine and cosine functions.
Laurent Series yield Fourier Series
A difficult thing to understand and/or motivate is the fact that arbitrary periodic functions have Fourier series representations. In this section, we prove that periodic analytic functions have such a representation using Laurent expansions.
Fourier Analysis for Periodic Functions
The Fourier series representation of analytic functions is derived from Laurent expansions. The elementary complex analysis is used to derive additional fundamental results in the harmonic analysis including the representation of C∞ periodic functions by Fourier series, the representation of rapidly decreasing functions by Fourier integrals, and Shannon’s sampling theorem. The ideas are classical and of transcendent beauty.


A function is periodic of period L if f(x+L) = f(x) for all x in the domain of f. The smallest positive value of L is called the fundamental period.
The trigonometric functions sin x and cos x are examples of periodic functions with fundamental period 2π and tan x is periodic with fundamental period π. A constant function is a periodic function with arbitrary period L.
It is easy to verify that if the functions f1, . . . , fn are periodic of period L, then any linear combination
is also periodic. Furthermore, if the infinite series
consisting of 2L-periodic functions converges for all x, then the function to which it converges will be periodic of period 2L. There are two symmetry properties of functions that will be useful in the study of Fourier series.
Even and Odd Function
A function f(x) is said to be even if f(−x) = f(x).
The function f(x) is said to be odd if f(−x) = −f(x).
Graphically, even functions have symmetry about the y-axis, whereas odd functions have symmetry around the origin.

Examples:
Sums of odd powers of x are odd: 5x3 − 3x
Sums of even powers of x are even: −x6 + 4x4 + x2 − 3
Since x is odd, and cos x is even

The product of two odd functions is even: x sin x is even
The product of two even functions is even: x2cos x is even
The product of an even function and an odd function is
odd: sin x cos x is odd
Note:
To find a Fourier series, it is sufficient to calculate the integrals that give the coefficients a0, an, and bn and plug them into the big series formula.
Typically, f(x) will be piecewise-defined.
Big advantage that Fourier series have over Taylor series: the function f(x) can have discontinuities.
Fourier series Formula
The formula for the fourier series of the function f(x) in the interval [-L, L], i.e. -L ≤ x ≤ L is given by:

The above Fourier series formulas help in solving different types of problems easily.
Fourier Series Example
Example: Determine the fourier series of the function f(x) = 1 – x2 in the interval [-1, 1].
Solution:
Given,
f(x) = 1 – x2; [-1, 1]
We know that, the fourier series of the function f(x) in the interval [-L, L], i.e. -L ≤ x ≤ L is written as:
Applications
A Fourier Series has many applications in mathematical analysis as it is defined as the sum of multiple sines and cosines. Thus, it can be easily differentiated and integrated, which usually analyses the functions such as saw waves which are periodic signals in experimentation. It also provides an analytical approach to solve the discontinuity problem. In calculus, this helps in solving complex differential equations.
For more information, visit BYJU’S – The Learning App and register with the app to watch all the interactive videos to learn with ease.
Frequently Asked Questions – FAQs
What is the Fourier Series formula?
f(x) = A_0 + ∑_{n = 1}^{∞} A_n cos(nπx/L) + ∑_{n = 1}^{∞} B_n sin(nπx/L)
What is the Fourier series used for?
How do you solve a Fourier series?
Step 1: Multiply the given function by sine or cosine, then integrate
Step 2: Estimate for n=0, n=1, etc., to get the value of coefficients.
Step 3: Finally, substituting all the coefficients in Fourier formula.

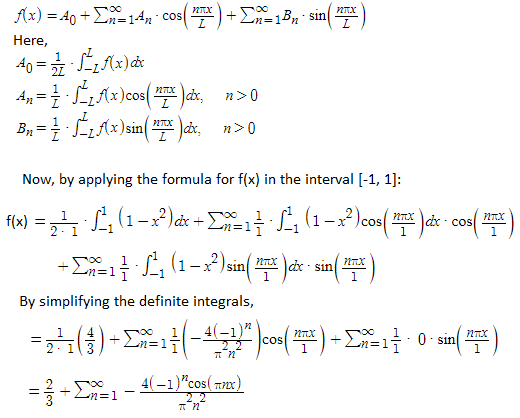
Comments