Number System Class 9 Notes - Chapter 1

CBSE Class 9 Maths Number System Notes

Download PDF

Introduction to Number Systems

The number system is the process of representing numbers on the number line using certain rules and symbols. A number line is a depiction of numbers on a straight line with a specified interval between them. The number system is used to do mathematical computations ranging from complex scientific calculations to counting the number of chocolates left in the box. In this article, we are going to discuss the Class 9 Maths Chapter 1 Number System.
To know more about Number System, visit here.

What Are Numbers?

Number: An arithmetical value representing a particular quantity. The various types of numbers are natural numbers, whole numbers, integers, rational numbers, irrational numbers, real numbers, etc.

To know more about Numbers, visit here.

Natural Numbers

Natural numbers(N) are positive numbers i.e. 1, 2, 3 and so on. Natural numbers are positive integers.

To know more about Natural Numbers, visit here.

Whole Numbers

Whole numbers (W) are 0, 1, 2 and so on. Whole numbers are all natural numbers, including ‘0’. Whole numbers do not include any fractions, negative numbers or decimals.
To know more about Whole Numbers, visit here.

Integers

Integers are numbers that include whole numbers along with negative numbers. An integer is a number from a set of negative and positive numbers, including zero, which has no decimal or fractional value. -3, 2, 0, 15, 900, etc., are examples of integers. Z is the symbol for a set of integers.

To know more about Integers, visit here.

Rational Numbers

A number ‘r’ is called a rational number if it can be written in the form p/q, where p and q are integers and q ≠ 0.
Some examples of rational numbers include 3/5, 7/2, 11/13, and so on.

To know more about Rational Numbers, visit here.

Irrational Numbers

Any number that cannot be expressed in the form of p/q, where p and q are integers and q≠0, is an irrational number. Examples: √2, 1.010024563…, e, π
To know more about Irrational Numbers, visit here.
Properties of Irrational Numbers
The following are the four properties of irrational numbers:
(i) Negative of an irrational number is an irrational number.
(ii) Sum and difference of a rational and an irrational number is always an irrational number.
(iii) Sum, product and difference of two irrational numbers is either a rational or irrational number.
(iv) Product of a rational number with an irrational number is either rational or irrational.

Real Numbers

Any number which can be represented on the number line is a real number(R). It includes both rational and irrational numbers. Every point on the number line represents a unique real number.
Examples of real numbers include -15, 3.14, 25, 22/7 and so on.
To know more about Real Numbers, visit here.

Also, read:

• Prime Numbers
• Composite Numbers
• Co Prime Numbers
• Even and Odd Numbers

For more information on Number Systems, watch the below video

Representation of Irrational Numbers on the Number Line

Let √x be an irrational number. To represent it on the number line we will follow the following steps:

• Take any point A. Draw a line AB = x units.
• Extend AB to point C such that BC = 1 unit.
• Find out the mid-point of AC and name it ‘O’. With ‘O’ as the centre draw a semi-circle with radius OC.
• Draw a straight line from B which is perpendicular to AC, such that it intersects the semi-circle at point D.

Length of BD=√x.

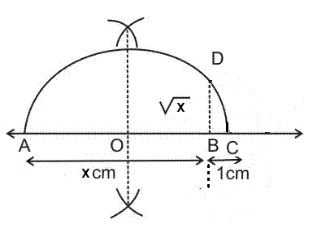
• With BD as the radius and origin as the centre, cut the positive side of the number line to get √x.

Identities for Irrational Numbers

Arithmetic operations between:

• Rational and irrational will give an irrational number. Example: 2 × √3 = 2√3 i.e. irrational.
• Irrational and irrational will give a rational or irrational number. Example: √3 × √3 = 3 which is rational

If a and b are real numbers,

• √(ab) = √a√b
• (√a+√b) (√a-√b) = a – b
• (a+√b)(a−√b) = a²−b
• (√a+√b)(√c+√d) = √ac+√ad+√bc+√bd
• (√a+√b)(√c−√d) = √ac−√ad+√bc−√bd
• (√a+√b)² = a+2√(ab)+b

Rationalisation

Rationalisation is the process of converting an irrational number into a rational number.
For example, the rationalisation of 1/√2 is:
1/√2 × √2/√2 = √2/2
We know that √2 = 1.414.
Hence, we can write it as
= 1.414/2, which can be easily represented on the number line.

Laws of Exponents for Real Numbers

If a, b, m and n are real numbers then:

• a^m × aⁿ= a^m+n
• (a^m) ⁿ = a^mn
• a^m/aⁿ = a^m−n, where (m > n)
• a^mb^m=(ab)^m

Here, a and b are the bases and m and n are exponents.

Decimal Representation of Rational Numbers

The decimal representation of a rational number is the process of converting a rational number into a decimal number. The converted decimal number should be equal to the given rational number. This process can be done with the help of the long division method. Once the rational numbers are converted into decimal values, we can easily represent them on the number line.

Decimal Expansion of Rational and Irrational Numbers

The decimal expansion of a rational number is either terminating or non-terminating and recurring.

Example: 1/2 = 0.5 , 1/3 = 3.33…….
The decimal expansion of an irrational number is non terminating and non-recurring.
Examples: √2 = 1.41421356..
To know more about decimal expansion of rational numbers, visit here.

Expressing Decimals as Rational Numbers

Case 1 – Terminating Decimals

Example: 0.625

Let x = 0.625

Step 1: If the number of digits after the decimal point is y, then multiply and divide the number by 10^y.

So, x = 0.625 × (1000/1000) = 625/1000.

Step 2: Reduce the obtained fraction to its simplest form.

Hence, x = 5/8

Case 2: Recurring Decimals

If the number is non-terminating and recurring, then we will follow the following steps to convert it into a rational number:

Step 1: Let x be the given recurring decimal

Step 2: Multiply the first equation with 10^y, where y is the number of digits that are recurring.

Multiply both sides of (1) by 100.

Step 3. Subtract equation (1) from equation (2).

On subtracting equation (1) from (2), we get

⇒ 99x = 103.2

⇒ x = 103.2/99 = 1032/990

Which is the required rational number.

Step 4: Reduce the obtained rational number to its simplest form.

Thus, x = 172/165.