Ratio –
A ratio is a quantitative relation of two amounts or numbers that can be expressed in the following ways-
Fraction- Such as 2/3, 3/5 etc.
With a colon – 2:3, 3:5 etc.
and with “to” between numbers. – 2 to 3, 3 to 5 etc.
Comparison of Ratios
Let us consider a problem statement to understand the concept of comparison of ratios.
Statement: An architect states that the buildings that have the ratio of span to height more than 1:4 is only feasible. The dimensions of the plans of various buildings are laid before him. See the table below.
Read: Ratio and Proportion
Let us find out the span to height ratios for all the buildings in the simplest form.

Building A = 3/5
Building B = 1/5
Building C = 1/3
Compare this with the ratio given by the architect.
For Building A,

The question mark above can be anything, >, < or =.
Cross multiplying the terms,
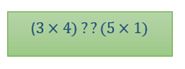
We get,
12 > 5
Hence we can say ratio ¾ is greater than¼. According to the problem statement, this satisfies the criteria as per the architect. Therefore Building A is feasible.
Similarly calculating for other buildings, for Building B, we find that 1/5 is less than ¼ and for Building C, 1/3 is greater than ¼. Hence Buildings A and C are feasible while building B is not feasible.
Concept of comparison of ratios is used for the design of aeroplanes to tall buildings to large ships.
| Let’s Work out-
Example: A dance club was given a target to increase the participation of boys with respect to girls in one year. At the start of the year, there were 40 boys and 100 girls and at the end of the year, there were 60 boys and 120 girls. Was the dance club successful in increasing the rate of participating? Solution: The ratio of boys to girls at the start of year = 40/100 = 2/5 The ratio of boys to girls at the end of year = 60/120 = ½ ½ is greater than 2/5. Hence the dance club was successful in increasing the rate of participation. |
For a detailed discussion on the comparison of ratios and proportions, download BYJU’S – The Learning App.

Comments