Finite and infinite sets are two of the different types of sets. The word ‘Finite’ itself describes that it is countable, and the word ‘Infinite’ means it is not finite or uncountable. Here, you will learn about finite and infinite sets, their definition, properties and other details of these two types of sets, along with various examples and questions.
Definition of Finite set
Finite sets are sets having a finite/countable number of members. Finite sets are also known as countable sets, as they can be counted. The process will run out of elements to list if the elements of this set have a finite number of members.
Examples of finite sets:
P = { 0, 3, 6, 9, …, 99}
Q = { a : a is an integer, 1 < a < 10}
A set of all English Alphabet (because it is countable).
Another example of a Finite set:
A set of months in a year.
M = {January, February, March, April, May, June, July, August, September, October, November, December}
n (M) = 12
It is a finite set because the number of elements is countable.
Cardinality of Finite Set
If ‘a’ represents the number of elements of set A, then the cardinality of a finite set is n(A) = a. The cardinality of a finite set is a natural number or possibly 0.
So, the Cardinality of set A of all English Alphabets is 26 because the number of elements (alphabets) is 26.
Hence, n (A) = 26.
Similarly, a set containing the months in a year will have a cardinality of 12.
So this way, we can list all the elements of any finite set and list them in the curly braces or Roster form.
Properties of Finite sets
The following finite set conditions are always finite.
- A subset of the Finite set
- The union of two finite sets
- The power set of a finite set
Few Examples:
P = {1, 2, 3, 4}
Q = {2, 4, 6, 8}
R = {2, 3)
- Here, all the P, Q, and R are finite sets because the elements are finite and countable.
- R ⊂ P, i.e., R is a Subset of P because all the elements of set R are present in P. So, the subset of a finite set is always finite.
- P U Q is { 1, 2, 3, 4, 6, 8}, so the union of two sets is also finite.
The number of elements of a power set = 2n.
The number of elements of the power set of set P is 24 = 16, as the number of elements of set P is 4. So it shows that the power set of a finite set is finite.
Non- Empty Finite set
It is a set where either the number of elements is big or only starting or ending is given. So, we denote it with the number of elements, n(A), and if n(A) is a natural number, then it’s a finite set.
Example:
S = { a set of the number of people living in India}
It is difficult to calculate the number of people living in India, but it’s somewhere a natural number. So, we can call it a non-empty finite set.
If N is a set of natural numbers less than n. So the cardinality of set N is n.
N = {1, 2, 3,….n}
X = x1, x2, ……, xn
Y = {x : xi ϵ N, 1 < i < n}, where i is the integer between 1 and n.
Can we say that an empty set is a finite set?
Let’s learn what is an empty set first.
An empty set is a set with no elements and can be represented as { } and shows that it has no element.
P = { } Or ∅
As the finite set has a countable number of elements and the empty set has zero elements so, it is a definite number of elements.
So, with a cardinality of zero, an empty set is a finite set.
What is an Infinite set?
If a set is not finite, it is called an infinite set because the number of elements in that set is not countable, and also we cannot represent it in Roster form. Thus, infinite sets are also known as uncountable sets.
So, the elements of an Infinite set are represented by 3 dots (ellipse) thus, it represents the infinity of that set.
Examples of Infinite Sets
- A set of all whole numbers, W= {0, 1, 2, 3, 4,…}
- A set of all points on a line
- The set of all integers
Cardinality of Infinite Sets
The cardinality of a set is n (A) = x, where x is the number of elements of a set A. The cardinality of an infinite set is n (A) = ∞ as the number of elements is unlimited in it.
Properties of Infinite Sets
- The union of two infinite sets is infinite
- The power set of an infinite set is infinite
- The superset of an infinite set is also infinite
Comparison of Finite and Infinite Sets:
Let’s compare the differences between the Finite and Infinite sets:
The sets could be equal only if their elements are the same, so a set could be equal only if it is a finite set, whereas if the elements are not comparable, the set is infinite.
| Factors | Finite sets | Infinite sets |
|---|---|---|
| Number of elements | Elements are countable | The number of elements is uncountable |
| Continuity | It has start and end elements | It is endless from start or end. Both sides could have continuity |
| Cardinality | n(A) = n, n is the number of elements in the set | n(A) = ∞ as the number of elements are uncountable |
| union | The union of two finite sets is finite | The union of two infinite sets is infinite |
| Power set | The power set of a finite set is also finite | The power set of an infinite set is infinite |
| Roster form | Can be easily represented in roster form | As the set is infinite set can’t be represented in Roster form, so we use three dots to represent the infinity |
How to know if a Set is Finite or Infinite?
As we know, if a set has a starting and ending point, it is a finite set, but it is infinite if it has no end from any side or both sides.
Points to identify a set is whether a finite or infinite are:
- An infinite set is endless from the start or end, but both sides could have continuity, unlike in a Finite set where both start and end elements are there.
- If a set has an unlimited number of elements, it is infinite, and if the elements are countable, it is finite.
Graphical Representation of Finite and Infinite Sets
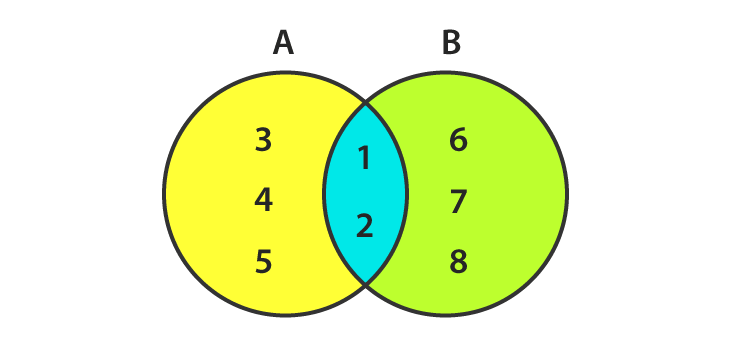
Here in the above picture,
A = {1, 2, 3, 4, 5}
B = {1, 2, 6, 7, 8}
A U B = {1, 2, 3, 4, 5, 6, 7, 8}
A∩B = {1, 2}
Both A and B are finite sets as they have a limited number of elements.
n(A) = 5 and n(B) = 5
AUB and A∩B are also finite.
So, a Venn diagram can represent the finite set, but it is difficult to do the same for an infinite set as the number of elements can’t be counted and bounced in a circle.
Video Lesson – What Sets are?

Read More:
| Universal Set | Power Set |
| Set Operations: Intersection And Difference Of Two Sets | Set Formulas |
| Union And Intersection Of Sets | Sets For Class 11 |
Now you have learned about Finite and Infinite sets in maths—download the BYJU’S for learning other concepts interestingly and efficiently.


Nice app
Bravo. I love your elucidation.