The standard equation of a circle is given by:
(x-h)2 + (y-k)2 = r2
Where (h,k) is the coordinates of center of the circle and r is the radius.
Before deriving the equation of a circle, let us focus on what is a circle? A circle is a set of all points which are equally spaced from a fixed point in a plane. The fixed point is called the center of the circle. The distance between the center and any point on the circumference is called the radius of the circle. In this article, we are going to discuss what is an equation of a circle formula in standard form, and find the equation of a circle when the center is the origin and the center is not an origin with examples.
| Table of Contents: |
What is the Equation of a Circle?
A circle is a closed curve that is drawn from the fixed point called the center, in which all the points on the curve are having the same distance from the center point of the center. The equation of a circle with (h, k) center and r radius is given by:
(x-h)2 + (y-k)2 = r2
This is the standard form of the equation. Thus, if we know the coordinates of the center of the circle and its radius as well, we can easily find its equation.
Example: Say point (1,2) is the center of the circle and radius is equal to 4 cm. Then the equation of this circle will be:
(x-1)2+(y-2)2 = 42
(x2−2x+1)+(y2−4y+4) =16
X2+y2−2x−4y-11 = 0
Function or Not
We know that there is a question that arises in case of circle whether being a function or not. It is clear that a circle is not a function. Because, a function is defined by each value in the domain is exactly associated with one point in the codomain, but a line that passes through the circle, intersects the line at two points on the surface.
The mathematical way to describe the circle is an equation. Here, the equation of the circle is provided in all the forms such as general form, standard form along with examples.
Equation of a Circle When the Centre is Origin
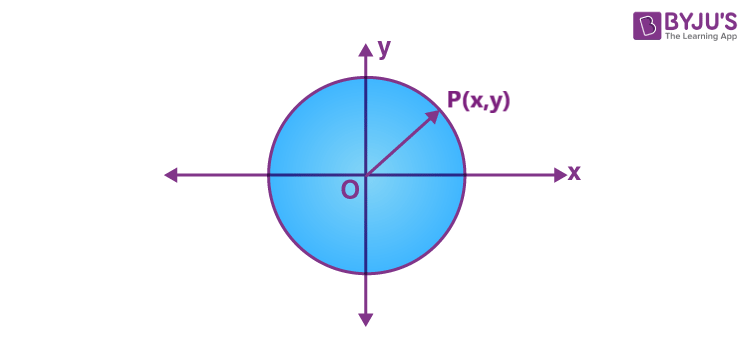
Consider an arbitrary point P(x, y) on the circle. Let ‘a’ be the radius of the circle which is equal to OP.
We know that the distance between the point (x, y) and origin (0,0)can be found using the distance formula which is equal to-
√[x2+ y2]= a
Therefore, the equation of a circle, with the center as the origin is,
x2+y2= a2
Where “a” is the radius of the circle.
Alternative Method
Let us derive in another way. Suppose (x,y) is a point on a circle, and the center of the circle is at origin (0,0). Now if we draw a perpendicular from point (x,y) to the x-axis, then we get a right triangle, where radius of the circle is the hypotenuse. The base of the triangle is the distance along x-axis and height is the distance along the y-axis. Thus, by applying the Pythagoras theorem here, we get:
Equation of a Circle When the Centre is not an Origin
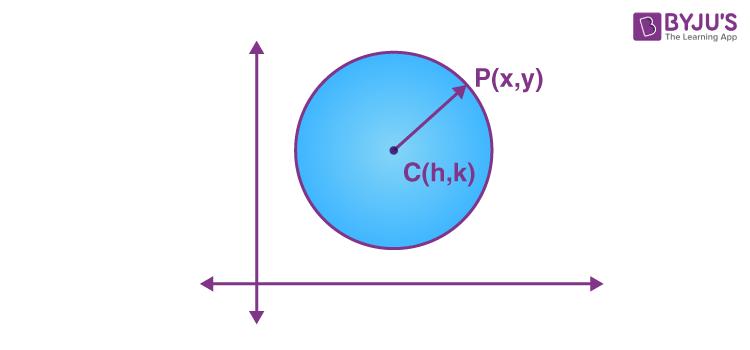
Let C(h, k) be the centre of the circle and P(x, y) be any point on the circle.
Therefore, the radius of a circle is CP.
By using distance formula,
(x-h)2 + (y-k)2 = CP2
Let radius be ‘a’.
Therefore, the equation of the circle with center (h, k)and the radius ‘a’ is,
(x-h)2+(y-k)2 = a2
which is called the standard form for the equation of a circle.
General form of Equation of a Circle
The general equation of any type of circle is represented by:
x2 + y2 + 2gx + 2fy + c = 0, for all values of g, f and c.
Adding g2 + f2 on both sides of the equation gives,
x2 + 2gx + g2+ y2 + 2fy + f2= g2 + f2 − c ………………(1)
Since, (x+g)2 = x2+ 2gx + g2 and (y+f)2 =y2 + 2fy + f2 substituting the values in equation (1), we have
(x+g)2+ (y+f)2 = g2 + f2−c …………….(2)
Comparing (2) with (x−h)2 + (y−k)2 = a2, where (h, k) is the center and ‘a’ is the radius of the circle.
h=−g, k=−f
a2 = g2+ f2−c
Therefore,
x2 + y2 + 2gx + 2fy + c = 0, represents the circle with centre (−g,−f) and radius equal to a2 = g2 + f2− c.
- If g2 + f2 > c, then the radius of the circle is real.
- If g2 + f2 = c, then the radius of the circle is zero which tells us that the circle is a point that coincides with the center. Such a type of circle is called a point circle
- g2 + f2 <c, then the radius of the circle become imaginary. Therefore, it is a circle having a real center and imaginary radius.
Polar Equation of a Circle
To find the polar form of equation of a circle, replace the value of x = r cos θ and y = r sin θ, in x2 + y2 = a2.
Hence, we get;
(r cos θ)2 + (r sin θ)2 = a2
r2 cos2 θ + r2 sin2 θ = a2
r2 (cos2 θ + sin2 θ) = a2
r2 (1) = a2 [Using trigonometry identity]
r = a
is the polar equation of a circle with radius a and center at the origin (0,0).
Video Lessons on Circles
Introduction to Circles

Parts of a Circle

Area of a Circle

All about Circles

Other Circle Formulas
Here are some formulas are given for circle in terms of radius.
| Diameter | 2 x radius |
| Circumference | 2π (radius) |
| Area | π(radius)2 |
How to Find the Equation of the Circle?
To find the equation of a circle given the radius and center of the circle, we can directly put the values in the standard form of the equation.
(x-h)2 + (y-k)2 = r2
Here, some solved problems are given to find the equation of a circle in both cases such as when the center of a circle is origin and center is not an origin is given below.
Solved Examples
Example 1:
Consider a circle whose center is at the origin and radius is equal to 8 units.
Solution:
Given: Centre is (0, 0), radius is 8 units.
We know that the equation of a circle when the center is origin:
x2+ y2 = a2
For the given condition, the equation of a circle is given as
x2 + y2 = 82
x2 + y2= 64, which is the equation of a circle
Example 2:
Find the equation of the circle whose center is (3,5) and the radius is 4 units.
Solution:
Here, the center of the circle is not an origin.
Therefore, the general equation of the circle is,
(x-3)2 + (y-5)2 = 42
x2 – 6x + 9 + y2 -10y +25 = 16
x2 +y2 -6x -10y + 18 =0
Example 3:
Equation of a circle is x2+y2−12x−16y+19=0. Find the center and radius of the circle.
Solution:
Given equation is of the form x2+ y2 + 2gx + 2fy + c = 0,
2g = −12, 2f = −16,c = 19
g = −6,f = −8
Centre of the circle is (6,8)
Radius of the circle = √[(−6)2 + (−8)2 − 19 ]= √[100 − 19] =
= √81 = 9 units.
Therefore, the radius of the circle is 9 units.
Related Articles |
Practice Questions on Equation of Circle
- Find the equation of a circle of radius 5 units, whose centre lies on the x-axis and which passes through the point (2, 3).
- Find the equation of a circle with the centre (h, k) and touching the x-axis.
- Show that the equation x2 + y2 – 6x + 4y – 36 = 0 represents a circle. Also, find the centre and radius of the circle.
To know more about circles download BYJU’S – The Learning App to learn with ease.
Frequently Asked Questions on Equation of a Circle
What is the equation for a circle?
(x-h)2+(y-k)2 = a2
Where (h,k) is the center and a is the radius of the circle.
What are the formulas for circles?
The area of a circle is equal to the pi of radius-squared.
What is the equation of a circle when the center is at the origin?
(x-0)2 + (y-0)2 = r2
x2 + y2 = r2
If (x-4)2+(y+7)2=9 is the equation of circle, then what is the center of circle?
(x-h)2+(y-k)2 = a2
h=4 and y = -7
Therefore, (4,-7) is the center of circle


Comments