CBSE Class 10 Maths Circles Notes:-Download PDF Here
A brief introduction to circles for Class 10 is provided here. Get the complete description provided here to learn about the concept of the circle. Also, learn how to draw a tangent to the circle with various theorems and examples.
The Class 10 Maths Chapter 10, ‘Circles’, covers concepts such as introduction to the circles, tangent to a circle, and the number of tangents from a point on a circle.
Click on the below link to access the solutions for Class 10 Maths Chapter 10.
Introduction to Circles
As we know that a circle is a closed two-dimensional geometrical figure, such that all points on the surface of a circle are equidistant from the point called the “centre”. The distance from the centre to any point on the surface of a circle is called “Radius”.

For more information on Circles, watch the below videos


To know more about Circles, visit here.
Circle and Line in a Plane
For a circle and a line on a plane, there can be three possibilities.
i) they can be non-intersecting
ii) they can have a single common point: in this case, the line touches the circle.
ii) they can have two common points: in this case, the line cuts the circle.
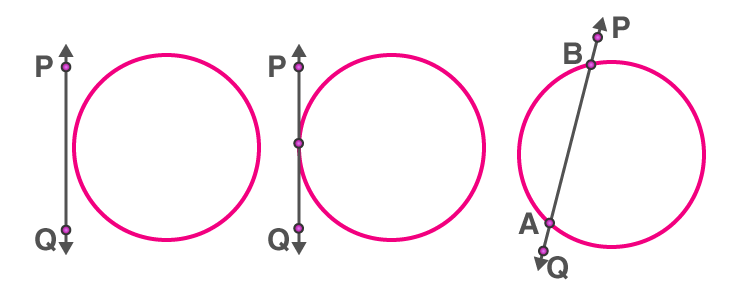
(i) Non-intersecting (ii) Touching (iii) Intersecting
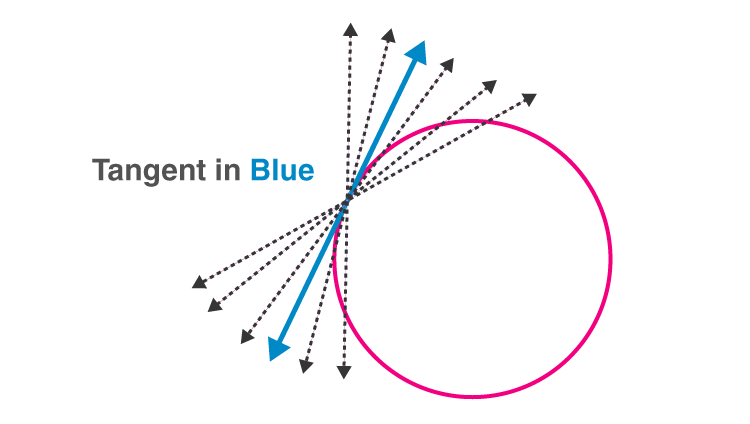
Tangent
A tangent to a circle is a line that touches the circle at exactly one point. For every point on the circle, there is a unique tangent passing through it.
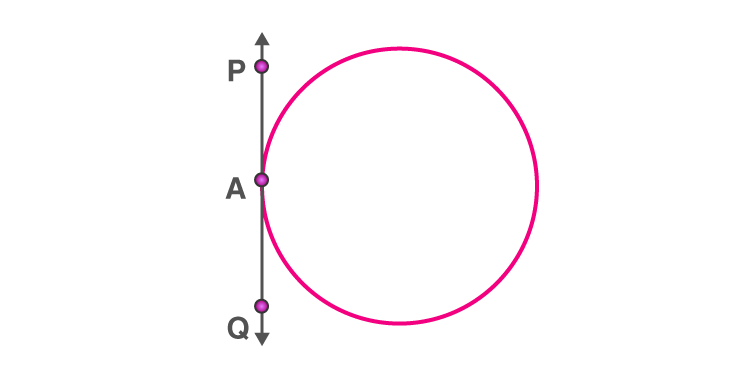
Tangent
To know more about Tangent, visit here.
Secant
A secant to a circle is a line that has two points in common with the circle. It cuts the circle at two points, forming a chord of the circle.
Secant
To know more about Secant, visit here.
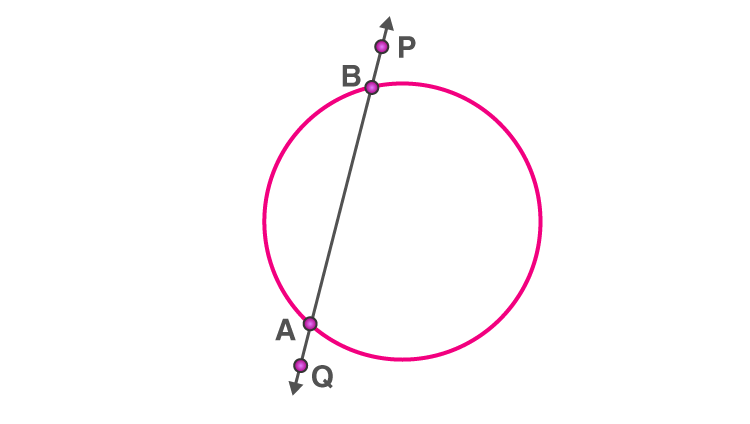
Tangent as a Special Case of Secant
Tangent as a special case of Secant
The tangent to a circle can be seen as a special case of the secant when the two endpoints of its corresponding chord coincide.
Two Parallel Tangents at most for a Given Secant
For every given secant of a circle, there are exactly two tangents which are parallel to it and touches the circle at two diametrically opposite points.
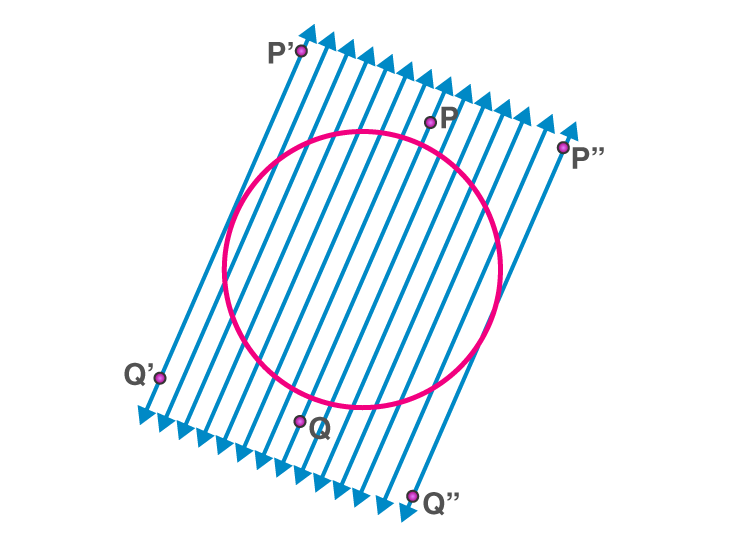
Parallel tangents
From the given diagram, we can observe the following points:
- PQ is the secant of a circle.
- P’Q’ & P”Q” are two tangents which are parallel to PQ.
Theorems
Tangent Perpendicular to the Radius at the Point of Contact
Theorem: The theorem states that “the tangent to the circle at any point is the perpendicular to the radius of the circle that passes through the point of contact”.
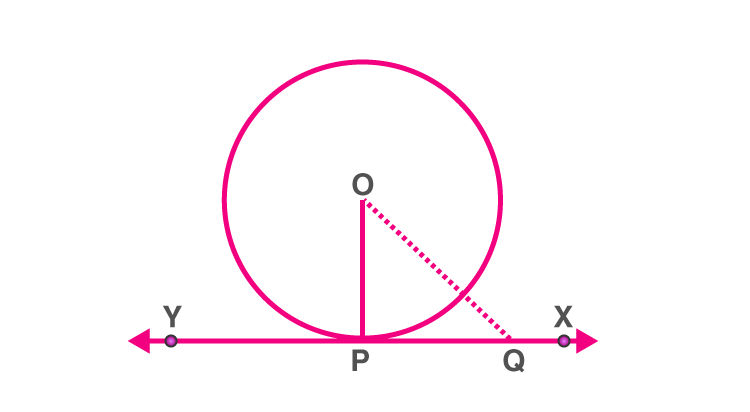
Tangent and radius
Here, O is the centre and OP⊥XY.
Theorem Proof:
Assume a circle with centre “O” and XY being the tangent to the circle at point “P”. Now, we have to prove that OP is perpendicular to the tangent XY.
Now, consider a point Q on the tangent line XY, other than P. Join the points OQ as shown in the figure.
Here, point Q should lie outside the circle. Because if the point Q lies inside the circle, XY will not be a tangent to the circle. It means that XY will become a secant of a circle.
So, OQ should be greater than the radius of the circle OP.
It means that
OQ > OP
As, this condition is obeyed for all points on line XY except P, OP should be the shortest of all distances from the centre of the circle “O” to the points of line XY.
Thus, we can conclude that OP is perpendicular to XY.
Hence, the theorem is proved.
For more information on Perpendicular Tangent Theorem, watch the below video

The Number of Tangents Drawn from a Given Point
i) If the point is in an interior region of the circle, any line through that point will be a secant. So, no tangent can be drawn to a circle which passes through a point that lies inside it.
No tangent can be drawn to a circle from a point inside it
ii) When a point of tangency lies on the circle, there is exactly one tangent to a circle that passes through it.
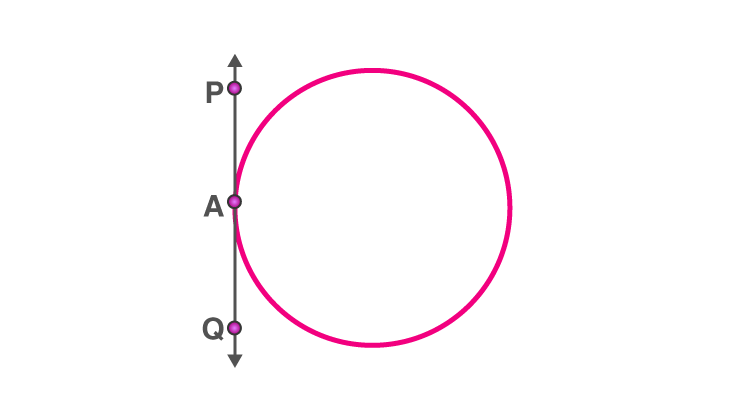
A tangent passing through a point lying on the circle
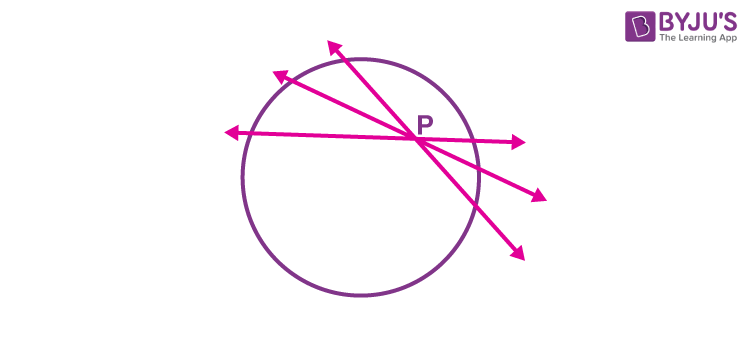
iii) When the point lies outside of the circle, there are accurately two tangents to a circle through it

Tangents to a circle from an external point
Length of a Tangent
The length of the tangent from the point (Say P) to the circle is defined as the segment of the tangent from the external point P to the point of tangency I with the circle. In this case, PI is the tangent length.
Lengths of Tangents Drawn from an External Point
Theorem: “The lengths of tangents drawn from an external point to a circle are equal.”
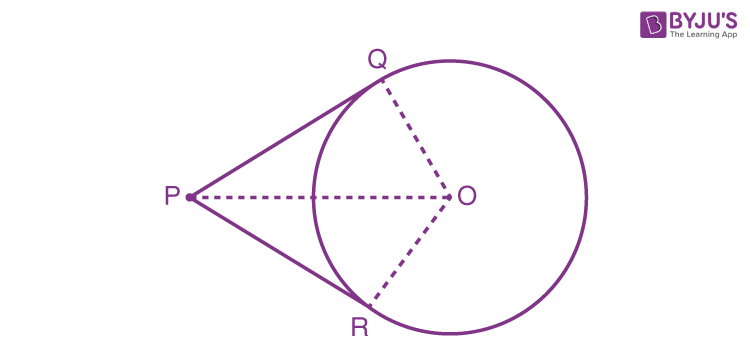
Tangents to a circle from an external point
Assume that we are provided with a circle whose centre is “O” and P is the point that lies outside the circle.
The two tangents formed here are PQ ad PR on the circle from the point P as shown in the figure.
Now, we have to prove PQ = PR.
To prove this, now we have to join OP, OQ, and OR.
According to the theorem “The tangent to the circle at any point is perpendicular to the radius of the circle that passes through the point of contact”, the angles formed between the tangents and radii are right angles.
So, two right angles are formed, such as ∠OQP and ∠ORP.
Thus, from the radii of the same circle, we can write OQ = OR.
Common side: OP = OP.
Hence, using the RHS congruence rule,
∆ OQP ≅ ∆ ORP
Thus, it gives PQ = PR [Using CPCT].
Hence the theorem is proved.
Thus, the two important theorems in Class 10 Maths Chapter 10 Circles are:
Theorem 10.1: The tangent at any point of a circle is perpendicular to the radius through the point of contact.
Theorem 10.2: The lengths of tangents drawn from an external point to a circle are equal.
Interesting facts about Circles and its properties are listed below:
- In two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
- The tangents drawn at the ends of a diameter of a circle are parallel.
- The perpendicular at the point of contact to the tangent to a circle passes through the centre.
- The angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
- The parallelogram circumscribing a circle is a rhombus.
- The opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
To know more about Tangent Circle, visit here.
Solved Question on Circles
Question 1:
Let there be a point P exterior to the circle with the centre at O such that OP = 10cm. If PT is tangent to the circle of length 8 cm. Find the radius of the circle.
Solution:
Given OP = 10 cm and PT = 8 cm. If we join OT, then OT is perpendicular to PT. By the theorem, “the tangent to the circle at any point is perpendicular to the radius of the circle that passes through the point of contact”.
Thus, triangle OTP is right triangle, right-angled at ∠T, by Pythagoras’ Theorem,
OP2 = OT2 + PT2
⇒ OT = √(OP2 – PT2) = √(102 – 82) = √(100 – 64) = √36 = 6 cm.
Therefore, the radius of the circle is 6 cm.
Question 2:
From a point P outside a circle with centre O, tangents PA and PB are drawn to the circle. Prove that OP is the right bisector of the segment AB.
Solution:
PA and PB are tangents from a common external point, then by the theorem, “Two tangents are of equal length when the tangent is drawn from an external point to a circle.”
PA = PB….(i)
Let us join AB and OP, where O is the centre of the circle, and M be the point of intersection of AB and OP. We shall prove that ∠PMA = ∠PMB = 90o.
In triangle PMA and PMB
PM = PM (common side)
PA = PB (from (i))
∠MPA = ∠MPB [since, tangents from an external point are equally inclines to the line segment joining that external point to the centre; ∠OPA = ∠OPB]
∴ △PMA ≅ △PMB [by SAS congruency]
So, MA = MB [c.p.c.t]
And ∠PMA = ∠PMB [c.p.c.t]
But ∠PMA + ∠PMB = 180o
∴ ∠PMA = ∠PMB = 90o.
Hence, OP is the right bisector of AB.
Question 3:
Prove that the tangents drawn at the ends of a diameter of a circle are parallel to each other.
Solution:
Let there be a circle with a centre at O and diameter AB. At A, CD is the tangent to the circle and at B, EF is the tangent to the circle.
We shall prove that CD || EF.
Now, OA ⟂ CD and OB ⟂ EF
[radius of the circle is perpendicular to the tangent at the point of contact]Hence, between CD and EF, the alternate interior angles are equal (is of 90o).
⇒ CD || EF [if the alternate angles are equal then lines are parallel].
|
Also Access: |
|
CBSE Class 10 Maths Chapter 9 Some Applications of Trigonometry Notes |
|
NCERT Exemplar Solutions for Class 10 Maths Chapter 9 Circles |


Sslc maths important question and answered
https://byjus.com/maths/important-questions-class-10-maths/
Thank you for ur notes. really helpfull
it was nice, like really nice
Thank you so much for notes. It was very useful to me. 😍😊
Thank you so much BYJUS for providing such important and helpful notes !!
These are helpful for my last day revisionThank you