CBSE Class 10 Maths Some Application of Trigonometry Notes:-Download PDF Here
Introduction
In Chapter 9, “Some Applications of Trigonometry,” students in Class 10 will learn how to use trigonometry to determine the height and distance of different items without having to measure them. Trigonometry was once used by astronomers to compute the distance between the planets, the Earth and stars. In geography and navigation, trigonometry is most frequently used to identify the latitude and longitude of a specified position.
Students will be able to learn the concepts such as heights and distances, the line of sight, angle of elevation, horizontal line, and angle of depression in this chapter. Students can get to know the concepts very well by solving the problems. Using trigonometric ratios, all the numerical problems are solved in this chapter.
To get complete solutions for CBSE Class 10 Maths Chapter 9, Some Applications of Trigonometry, click on the below link.
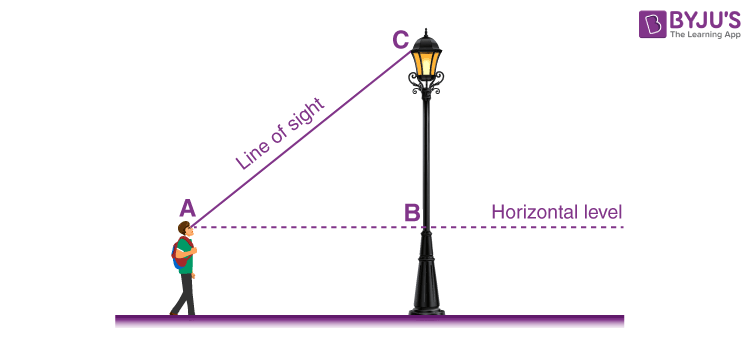
Horizontal Level and Line of Sight
Line of sight is the line drawn from the eye of the observer to the point on the object viewed by the observer.
The horizontal level is the horizontal line through the eye of the observer.
To know more about Height and Distance, visit here.
Angle of Elevation
The angle of elevation is relevant for objects above the horizontal level. It is the angle formed by the line of sight with the horizontal level. In the below-mentioned diagram, “θ” denotes the angle of elevation.

To know more about the Angle of elevation, visit here.
Angle of Depression
The angle of depression is relevant for objects below the horizontal level. It is the angle formed by the line of sight with the horizontal level.
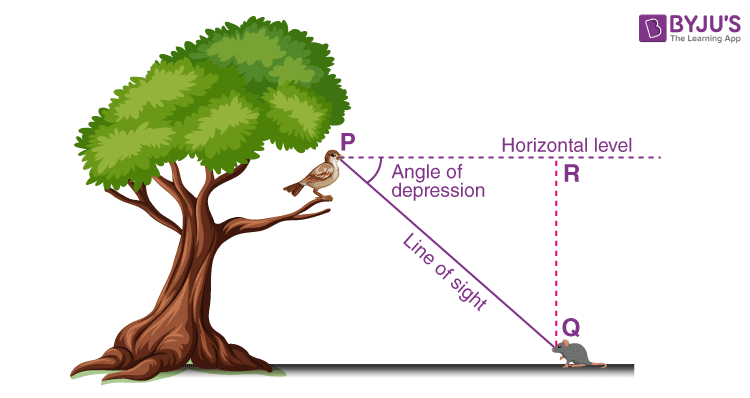
To know more about the Angle of depression, visit here.
Calculating Heights and Distances
To calculate heights and distances, we can make use of trigonometric ratios.
Go through the below trigonometric ratio table for reference:
| Trigonometry Ratios Table | ||||||||
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Angles (In Radians) | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
Step 1: Draw a line diagram corresponding to the problem.
Step 2: Mark all known heights, distances and angles and denote unknown lengths by variables.
Step 3: Use the values of various trigonometric ratios of the angles to obtain the unknown lengths from the known lengths.
Heights and Distance Summary
The below diagram gives the complete summary of “Heights and Distances”.

From the given diagram, if “C” is the point of observation,
- AC is the line of sight
- BC is the distance between the observer and the object.
- AB is the height of the object
- α is the angle of elevation
- β is the angle of depression.
To get solved problems on Heights and Distances, visit here.
For more information on Trigonometry – Measuring Heights And Distances, watch the below video

Be More Curious
Measuring the Distances of Celestial bodies with the Help of Trigonometry
Large distances can be measured by the parallax method. The parallax angle is half the angle between two lines of sight when an object is viewed from two different positions. Knowing the parallax angle and the distance between the two positions, large distances can be measured.
Solved Examples
Example 1: A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Solution:
Let A be the position of a kite at a height of 60 m above the ground.
Thus, AB = 60 m
Also, AC is the length of the string.
Angle of inclination = ∠ACB = 60

In right triangle ABC,
sin 60° = AB/AC
√3/2 = 60/AC
AC = (60 × 2)√/3
= (120 × √3)/(√3 × √3)
= (120√3)/3
= 40√3
Therefore, the length of the string is 40√3 m.
Example 2: A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30° as shown in the figure. Find the height of the tower and the width of the canal.

Solution:
Given,
AB is the height of the tower.
DC = 20 m (given)
In right ΔABD,
tan 30° = AB/BD
1/√3 = AB/(20 + BC)
AB = (20 + BC)/√3….(i)
In right ΔABC,
tan 60° = AB/BC
√3 = AB/BC
AB = √3 BC….(ii)
From (i) and (ii),
√3 BC = (20 + BC)/√3
3 BC = 20 + BC
2 BC = 20
BC = 10
Substituting the value of BC in equation (ii),
AB = (20 + 10)/√3 = 30/√3 = 10√3
Therefore, the height of the tower is 10√3 m, and the width of the canal is 10 m.
Practice Questions
- A spherical balloon of radius r subtends an angle θ at the eye of an observer. If the angle of elevation of its centre is φ, find the height of the centre of the balloon.
- From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
- A ladder 20 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 30° with the wall, find the height of the wall.


This is really very helpful me bcz I am getting previous problems also😊😊😊😔