The angle of depression is formed when the observer is higher than the object he/she is looking at. When an observer looks at an object that is situated at a distance lower than the observer, an angle is formed below the horizontal line drawn with the level of the eye of the observer and line joining object with the observer’s eye. Whereas the angle of elevation is the angle formed if a person stands on the ground and looks on the object kept above the ground at a height above the height of the person. This is the basic difference between the two angles. Both the angles are calculated by using the concept of trigonometry.
What is Angle of Depression?
The angle of depression is defined as an angle constructed by a horizontal line and the line joining the object and observer’s eye. This angle is dependent on two factors, i.e., height and distance. Let us learn about its definition, formula and real-life problems based on it.
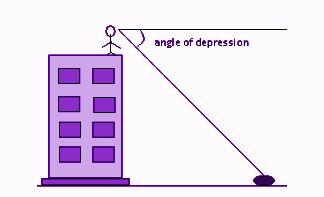
Angle of Depression Definition
The angle of depression is the angle between the horizontal line and the observation of the object from the horizontal line. It is basically used to get the distance of the two objects where the angles and an object’s distance from the ground are known to us. Its an angle that is formed with the horizontal line if the line of sight is downward from the horizontal line.
If the object observed by the observer is below the level of the observer, then the angle formed between the horizontal line and the observer’s line of sight is called the angle of depression. In the below figure, θ is the angle of depression.
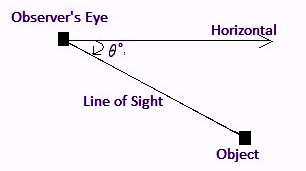
Angle of Depression Formula
With angles of elevation, if two of the sides of the right triangle are known, then the formula for the angle of depression is given as below:
Tan θ = Opposite Side/Adjacent Side
Or
θ = tan-1 (Opposite Side/Adjacent Side)
See the below diagram, where θ is the angle of inclination, such as,
∠ ABO = Angle of elevation
And
∠O = Angle of depression
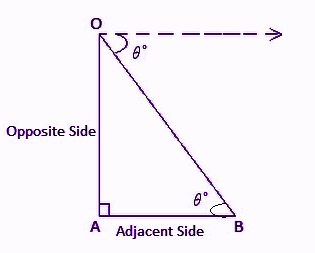
Hence, ∠ABO = ∠O = θ
Angle of Depression and Elevation comparison
The angle of elevation is just opposite to the angle of depression. The angle of elevation is formed when it is between the line of sight and the horizontal line. If the line of sight is above to the horizontal line, the angle formed is known as the angle of elevation. But in the angle of depression, the line of sight is downwards to the horizontal line. The figure that represents the angle of elevation is given below:

Angle of Depression Examples
Example 1:
The angle of depression of a vehicle from the top of a tower on the ground is 60. If the vehicle is away from the building at a distance of 100 meters, find the height of the tower.
Solution:
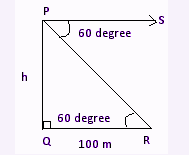
In the above figure,
R is a vehicle
PQ is the height of the tower
RQ is the distance between the tower and the vehicle
PS is the line of sight.
Given,
The angle of depression, ∠ SPR = 60°
So,
The angle of elevation, ∠ QRP = Angle of depression, ∠ SPR = 60°.
Now, in right triangle PQR,
QR = 100m
∠ R = 60°
PQ = h (in m)
Let ∠ R = θ = 60°
We know,
tan θ = (Opposite Side/Adjacent Side)
Tan 60 = PQ/RQ = h/100
√3 = h/100
Or
h = √3 x 100
h = 173.20 m
Hence, the height of the tower is 173.20 meters.
Example 2:
The angle of depression of a stone from the top of a tower on the ground is 45. If the stone is away from the building at a distance of 120 meters, find the height of the tower.
Solution:
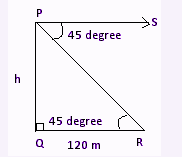
In the above figure,
R is a stone.
PQ is the height of the tower.
RQ is the distance between the tower and the stone.
PS is the line of sight.
Given, Angle of depression, ∠ SPR = 45°.
As we know,
Angle of elevation, ∠ QRP = Angle of depression, ∠ SPR = 45°.
Now, in right-angled triangle PQR, we know that;
QR = 120 m
∠ R = 45°,
PQ = h
Let ∠ R = θ = 45°
We know that,
tanθ = Opposite side/Adjacent side
Hence,
tan 45° = PQ/RQ = h/120
On cross multiplying, we get;
h = 120 x tan 45°
Since, tan 45 = 1
Therefore, h = 120 meters.
To learn more Mathematical concepts, register with BYJU’S – The Learning App and download the app today!
