We are familiar with the terms Domain of a Function and Range of a Function. But what does it mean? Before diving deeper into the topic, let us understand what a function is? Then, get into the detailed explanation of the domain, range and codomain of a function, along with solved examples.
| Table of Contents: |
Functions
Functions are one of the fundamental concepts in mathematics which have got numerous applications in the real world. Be it the mega skyscrapers or super-fast cars, their modelling requires methodical application of functions. Almost all real-world problems are formulated, interpreted, and solved using functions.
Relations:
An understanding of relations is required to learn functions, Knowledge of Cartesian products is also required to learn about relations in maths. A Cartesian product of two sets A and B is the collection of all the ordered pairs (a, b) such that a ∈ A and b ∈ B.
Learn: Cartesian product
A relation is a subset of a Cartesian product. Thus, a relation is a rule that “relates” an element from one set to another. A function is a special kind of relation. Let’s consider a relation F from A set A to B
Definition: A relation F is said to be a function if each element in set A is associated with exactly one element in set B.
To understand the difference between relations and functions with the help of an example.
Example
Set A = Names of all countries that won the cricket world cup
Set B = List of years in which the world cup played
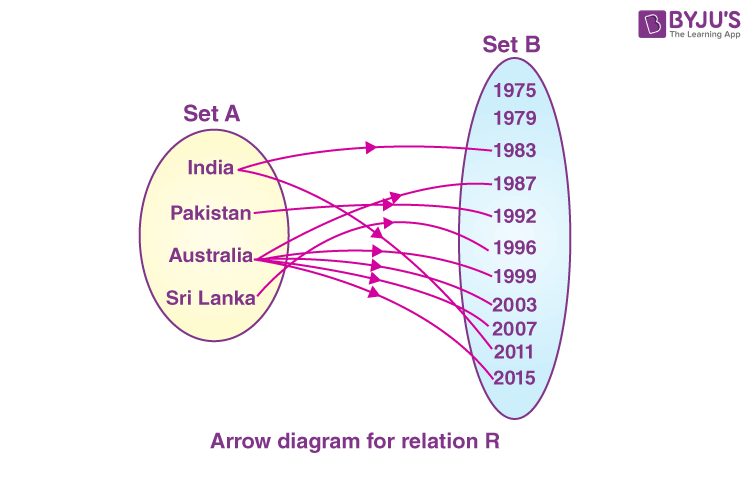
The arrow diagram shows (in the figure below) the relation R but not a function.
This is because elements of set A are associated with more than one element of set B.
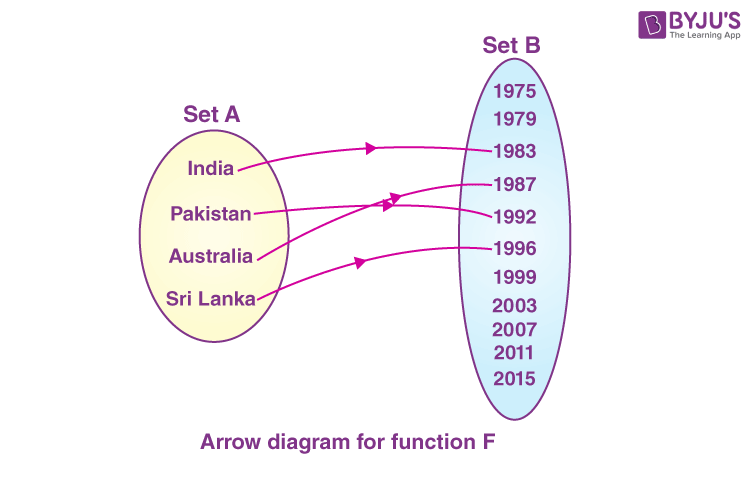
Suppose we define a relation F from set A to B such that it associates the countries with the year in which they won the world cup for the first time. Thus, every element in set A will be exactly associated with only one element in set B.
This relation F shown in the below figure is qualified to be a function.
Remember that in the case of a relation, the domain might not be the same as the left set in the arrow diagram. This is because the set may contain any element which doesn’t have an image in the right set. But in the case of functions, the domain will always be equal to the first set. Range and Codomain of a function are defined in the same way as they are defined for relations.
Domain and Range
The domain and range of a function can be identified based on the possibility of the given function to be defined in the real set. Let’s have a look at Domain and Range that is given in detail here.
Domain
The set of all possible values which qualify as inputs to a function is known as the domain of the function, or it can also be defined as the entire set of values possible for independent variables. The domain can be found in – the denominator of the fraction is not equal to zero and the digit under the square root bracket is positive. (In the case of a function with fraction values).
For e.g. the domain of the function F is set A i.e. {India, Pakistan, Australia, Sri Lanka}.
How to Find the Domain of a function
- To find the domain, we need to look at the values of the independent variables which are allowed to use as explained above, i.e. no zero at the bottom of the fraction and no negative sign inside the square root.
- In general, the set of all real numbers (R) is considered as the domain of a function subject to some restrictions. They are:
When the given function is of the form f(x) = 2x + 5 or f(x) = x2 – 2, the domain will be “the set of all real numbers.
When the given function is of the form f(x) = 1/(x – 1), the domain will be the set of all real numbers except 1. - In some cases, the interval be specified along with the function such as f(x) = 3x + 4, 2 < x < 12. Here, x can take the values between 2 and 12 as input (i.e. domain).
- Domain restrictions refer to the values for which the given function cannot be defined.
Also, try: Domain and Range Calculator
Range
The set of all the outputs of a function is known as the range of the function or after substituting the domain, the entire set of all values possible as outcomes of the dependent variable.
For e.g. the range of the function F is {1983, 1987, 1992, 1996}. On the other hand, the whole set B is known as the codomain of the function. It is the set that contains all the outputs of the function. So, the set of real numbers is a codomain for every real-valued function. The codomain of the function F is set B.
Video Lesson
Range of a Function

How to Find the Range of a Function
Consider a function y = f(x).
- The spread of all the y values from minimum to maximum is the range of the function.
- In the given expression of y, substitute all the values of x to check whether it is positive, negative or equal to other values.
- Find the minimum and maximum values for y.
- Then draw a graph for the same.
Codomain
In relations and functions, the codomain is the set of all possible outcomes of the given relation or function. Sometimes, the codomain is also equal to the range of the function. However, the range is the subset of the codomain.
An interesting point about the range and codomain is that “it is possible to restrict the range (i.e. the output of a function) by redefining the codomain of that function”. For example, the codomain of f(x) must be the set of all positive integers or negative real numbers and so on. Here, the output of the function must be a positive integer and the domain will also be restricted accordingly in this case.
Till now, we have represented functions with upper case letters but they are generally represented by lower case letters. If f is a function from set A to B and (a,b) ∈ f, then f(a) = b. b is called the image of a under f and a is called the preimage of b under f.
Summary:
- The domain is defined as the entire set of values possible for independent variables.
- The Range is found after substituting the possible x- values to find the y-values.
Solved Examples
Example 1:
Find the domain and range of a function f(x) = 3x2 – 5.
Solution:
Given function:
f(x) = 3x2 – 5
We know that the domain of a function is the set of input values for f, in which the function is real and defined.
The given function has no undefined values of x.
Thus, for the given function, the domain is the set of all real numbers.
Domain = [-∞, ∞]
Also, the range of a function comprises the set of values of a dependent variable for which the given function is defined.
Ley y = 3x2 – 5
3x2 = y + 5
x2 = (y + 5)/3
x = √[(y + 5)/3]
Square root function will be defined for non-negative values.
So, √[(y + 5)/3] ≥ 0
This is possible when y is greater than y ≥ -5.
Hence, the range of f(x) is [-5, ∞).
Example 2:
Find the domain and range of a function f(x) = (2x – 1)/(x + 4).
Solution:
Given function is:
f(x) = (2x – 1)/(x + 4)
We know that the domain of a function is the set of input values for f, in which the function is real and defined.
The given function is not defined when x + 4 = 0, i.e. x = -4
So, the domain of given function is the set of all real number except -4.
i.e. Domain = (-∞, -4) U (-4, ∞)
Also, the range of a function comprises the set of values of a dependent variable for which the given function is defined.
Let y = (2x – 1)/(x + 4)
xy + 4y = 2x – 1
2x – xy = 4y + 1
x(2 – y) = 4y + 1
x = (4y + 1)/(2 – y)
This is defined only when y is not equal to 2.
Hence, the range of the given function is (-∞, 2) U (2, ∞).
Practice Problems
- Find the domain and range of the function f(x) = 1/x.
- Write the domain set for this function f(x) = 1/(x3 − 3x2 − 6x − 8).
- What is the domain, codomain and range of the function f(x) = 4/√(x – 1).
Video Lesson
Domain, Range and Period of Function

There are several types of functions and some of them have got funny names e.g. floor function, ceiling function, etc. To know more, visit www.byjus.com and experience fun in learning.
Recommended Videos
Relations and Types of Relations

Functions – Introduction, Co-domain and Range

Functions and Types of Functions

Range of Functions – Concepts & Questions


Comments