Introduction to Mean, Median and Mode: Often in statistics, we tend to represent a set of data by a representative value which would approximately define the entire collection. This representative value is called the measure of central tendency, and the name suggests that it is a value around which the data is centred. These central tendencies are mean, median and mode.
| Table of Contents: |
We are all interested in cricket but have you ever wondered during the match why the run rate of the particular over is projected and what does the run rate mean? Or, when you get your examination result card, you mention the aggregate percentage. Again what is the meaning of aggregate? All these quantities in real life make it easy to represent a collection of data in terms of a single value. It is called Statistics.
Statistics deals with the collection of data and information for a particular purpose. The tabulation of each run for each ball in cricket gives the statistics of the game. The representation of any such data collection can be done in multiple ways, like through tables, graphs, pie-charts, bar graphs, pictorial representation etc.
Now consider a 50 over ODI match going between India and Australia. India scored 370 runs by the end of the first innings. How do you decide whether India put a good score or not? It’s pretty simple, right; you find the overall run rate, which is good for such a score. Thus, here comes the concept of mean, median and mode in the picture. Let us learn in detail each of the central tendencies.
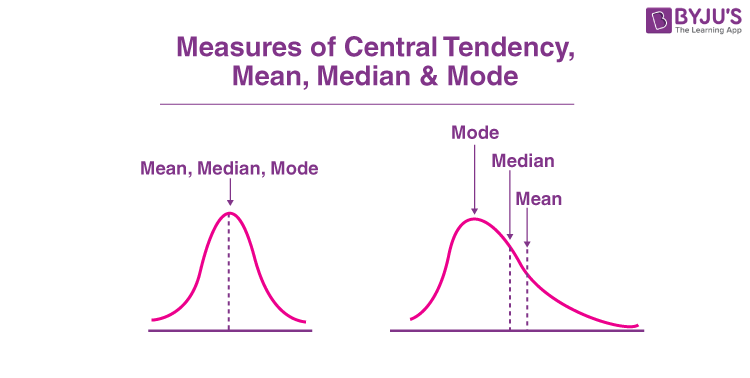
Measures of central tendency
The measures of central tendencies are given by various parameters but the most commonly used ones are mean, median and mode. These parameters are discussed below.
What is Mean?
Mean is the most commonly used measure of central tendency. It actually represents the average of the given collection of data. It is applicable for both continuous and discrete data.
It is equal to the sum of all the values in the collection of data divided by the total number of values.
Suppose we have n values in a set of data namely as x1, x2, x3, …, xn, then the mean of data is given by:
It can also be denoted as:
For grouped data, we can calculate the mean using three different methods of formula.
| Direct method | Assumed mean method | Step deviation method |
| Mean \(\begin{array}{l}\overline{x}=\frac{\sum_{i=1}^{n}f_ix_i}{\sum_{i=1}^{n}f_i}\end{array} \)
Here, ∑fi = Sum of all frequencies |
Mean \(\begin{array}{l}(\overline{x})=a+\frac{\sum f_id_i}{\sum f_i}\end{array} \)
Here, a = Assumed mean di = xi – a ∑fi = Sum of all frequencies |
Mean \(\begin{array}{l}(\overline{x})=a+h\frac{\sum f_iu_i}{\sum f_i}\end{array} \)
Here, a = Assumed mean ui = (xi – a)/h h = Class size ∑fi = Sum of all frequencies |
To learn more about the mean, visit here.
What is Median?
Generally median represents the mid-value of the given set of data when arranged in a particular order.
Median: Given that the data collection is arranged in ascending or descending order, the following method is applied:
- If number of values or observations in the given data is odd, then the median is given by [(n+1)/2]th observation.
- If in the given data set, the number of values or observations is even, then the median is given by the average of (n/2)th and [(n/2) +1]th observation.
The median for grouped data can be calculated using the formula,
To understand in detail about the median, visit here.
What is Mode?
The most frequent number occurring in the data set is known as the mode.
Consider the following data set which represents the marks obtained by different students in a subject.
| Name | Anmol | Kushagra | Garima | Ashwini | Geetika | Shakshi |
| Marks Obtained (out of 100) | 73 | 80 | 73 | 70 | 73 | 65 |
The maximum frequency observation is 73 ( as three students scored 73 marks), so the mode of the given data collection is 73.
We can calculate the mode for grouped data using the below formula:
Also, learn: Mode
Video Lessons
Mean Median and Mode

Measure of Central Tendency for an Ungrouped Data

Example of Mean, Median and Mode
Let us see the difference between the mean median and mode through an example.
Example: The given table shows the scores obtained by different players in a match. What is mean, median and mode of the given data?
| S.No | Name | Runs Scored |
| 1 | Sachin | 80 |
| 2 | Yuvraj | 52 |
| 3 | Virat | 40 |
| 4 | Sehwag | 52 |
| 5 | Rohit | 70 |
| 6 | Harbhajan | 1 |
| 7 | Dhoni | 6 |
Solution:
i) The mean is given by:
The mean of the given data is 43.
ii) To find out the median let us first arrange the given data in ascending order
| Name | Harbhajan | Dhoni | Virat | Yuvraj | Sehwag | Rohit | Sachin |
| Runs | 1 | 6 | 40 | 52 | 52 | 70 | 80 |
As the number of items in the data is odd. Hence, the median is [(n+1)/2]th observation.
⇒ Median = [(7+1)/2]th observation = 52
iii) Mode is the most frequent data, which is 52.
Relation of Mean Median Mode
The relation between mean, median and mode that means the three measures of central tendency for moderately skewed distribution is given the formula:
| Mode = 3 Median – 2 Mean |
This relation is also called an empirical relationship. This is used to find one of the measures when the other two measures are known to us for certain data. This relationship is rewritten in different forms by interchanging the LHS and RHS.
Range
In statistics, the range is the difference between the highest and lowest data value in the set. The formula is:
Range – Highest value – Lowest value
Solved Problem
Question: Find the mean, median, mode and range for the given data:
90, 94, 53, 68, 79, 94, 53, 65, 87, 90, 70, 69, 65, 89, 85, 53, 47, 61, 27, 80
Solution:
Given,
90, 94, 53, 68, 79, 94, 53, 65, 87, 90, 70, 69, 65, 89, 85, 53, 47, 61, 27, 80
Number of observations = 20
Mean = (Sum of observations)/ Number of observations
= (90 + 94 + 53 + 68 + 79 + 94 + 53 + 65 + 87 + 90 + 70 + 69 + 65 + 89 + 85 + 53 + 47 + 61 + 27 + 80)/20
= 1419/20
= 70.95
Therefore, mean is 70.95.
Median:
The ascending order of given observations is:
27, 47, 53, 53, 53, 61, 65, 65, 68, 69, 70, 79, 80, 85, 87, 89, 90, 90, 94,94
Here, n = 20
Median = 1/2 [(n/2) + (n/2 + 1)]th observation
= 1/2 [10 + 11]th observation
= 1/2 (69 + 70)
= 139/2
= 69.5
Thus, the median is 69.5.
Mode:
The most frequently occurred value in the given data is 53.
Therefore, mode = 53
Range = Highest value – Lowest value
= 94 – 27
Practice Questions
- The points scored by a Kabaddi team in a series of matches are as follows:
17, 2, 7, 27, 15, 5, 14, 8, 10, 24, 48, 10, 8, 7, 18, 28
Find the mean, median and mode of the points scored by the team. - The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x. 29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
- A survey conducted on 20 households in a locality by a group of students resulted in the following frequency table for the number of family members in a household:
family size 1 – 3 3 – 5 5 – 7 7 – 9 9 – 11 Number of families 7 8 2 2 1 Find the mode of this data.
To know more about Measures of central tendency and the applications of Mean, Median and Mode with solved examples stay tuned with BYJU’S.

Frequently Asked Questions – FAQs
What is the mean median and mode?
How do you find the mean?
Mean = Sum of observations/Number of observations
In the case of grouped data, the mean is calculated using three methods such as:
Direct method
Assumed mean method
Step deviation method
How do I calculate the median?
Median = (n + 1)/2th observation {when n is odd}
Median = Average of (n/2)th and [(n/2) + 1]th observations {when n is even}
Median for grouped data = l + [(N/2 – cf)/f] × h
How do I calculate mode?
For grouped data, mode = l + [(f_1 – f_0)/(2f_1 – f_0 – f_2)] × h
What is the relation between mean mode median?
Mode = 3 Median – 2 Mean



Comments