In statistics, for a moderately skewed distribution, there exists a relation between mean, median and mode. This mean median and mode relationship is known as the “empirical relationship” which is defined as Mode is equal to the difference between 3 times the median and 2 times the mean. This relation has been discussed in detail below.
To recall,
- Mean is the average of the data set which is calculated by adding all the data values together and dividing it by the total number of data sets.
- Median is the middle value among the observed set of values and is calculated by arranging the values in ascending order or in descending order and then choosing the middle value.
- Mode is the number from a data set which has the highest frequency and is calculated by counting the number of times each data value occurs.
Empirical Relationship between Mean, Median and Mode
In case of a moderately skewed distribution, the difference between mean and mode is almost equal to three times the difference between the mean and median. Thus, the empirical mean median mode relation is given as:
| Mean – Mode = 3 (Mean – Median) |
Or
| Mode = 3 Median – 2 Mean |
Either of these two ways of equations can be used as per the convenience since by expanding the first representation we get the second one as shown below:
Mean – Mode = 3 (Mean – Median)
Mean – Mode = 3 Mean – 3 Median
By rearranging the terms,
Mode = Mean – 3 Mean + 3 Median
Mode = 3 Median – 2 Mean
However, we can define the relation between mean, median and mode for different types of distributions as explained below:
Mean Median Mode Relation With Frequency Distribution
- Frequency Distribution with Symmetrical Frequency Curve
If a frequency distribution graph has a symmetrical frequency curve, then mean, median and mode will be equal.
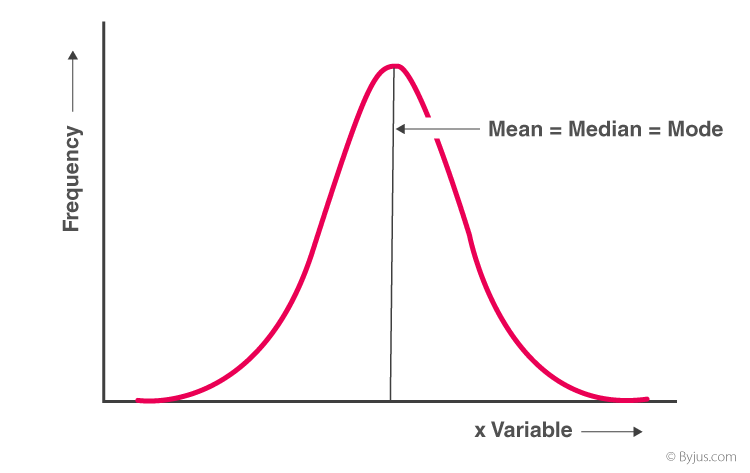
| Mean = Median = Mode |
- For Positively Skewed Frequency Distribution
In case of a positively skewed frequency distribution, the mean is always greater than median and the median is always greater than the mode.
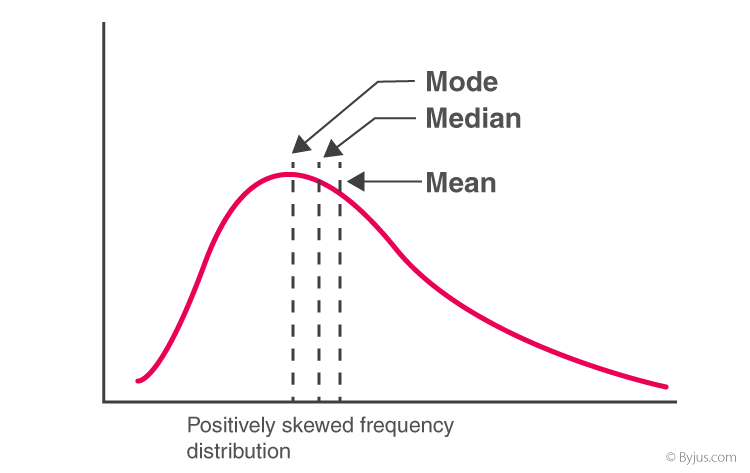
| Mean > Median > Mode |
- For Negatively Skewed Frequency Distribution
In case of a negatively skewed frequency distribution, the mean is always lesser than median and the median is always lesser than the mode.

| Mean < Median < Mode |
Also Check: Mean Median Mode Formula
Example Question Using the Mean, Median and Mode Relationship
Question: In a moderately skewed distribution, the median is 20 and the mean is 22.5. Using these values, find the approximate value of the mode.
Solution:
Given,
Mean = 22.5
Median = 20
Mode = x
Now, using the relationship between mean mode and median we get,
(Mean – Mode) = 3 (Mean – Median)
So,
22.5 – x = 3 (22.5 – 20)
22.5 – x = 7.5
∴ x = 15
So, Mode = 15.
Video Lesson on Median of Data

Read More:
| Mode Of Data & Statistics | Median |
| Median Of Data And Statistics | Difference Between Average and Mean |
Keep visiting BYJU’S to learn more such different maths articles. Also, register now to download various maths materials like sample papers, question papers, NCERT solutions and get several video lessons to learn more effectively.
Frequently Asked Questions – FAQs
What is the meaning of mean, median and mode?
What is empirical relationship between mean median and mode?
Mean – Mode = 3 (Mean – Median)
Or
Mode = 3 Median – 2 Mean
What is the relation between mean median and mode for a frequency distribution with symmetrical frequency curve?
Mean = Median = Mode
What is the relation between mean median and mode for a positively skewed frequency distribution?
Mean > Median > Mode
What is the relation between mean median and mode for a negatively skewed frequency distribution?
Mean < Median < Mode


Very good, this is going to be useful for some central tendency estimator I need to implement. Thanks!
Simple and good explanation.
Waoo Amazing i like it.