Modes of Heat Transfer (Conduction Examples)

In our everyday life, it has been observed that when a pan full of water is boiled on a flame, its temperature increases, but when the flame is turned off, it slowly cools down.

Table of Contents

• What are the different Modes of Heat Transfer?
• Recommended Videos
• Factors Affecting Heat Transfer
• Frequently Asked Questions – FAQs

What are the different Modes of Heat Transfer?

This is because of the phenomenon of heat transfer taking place between the pan full of water and the flame. It has been established that heat transfer takes place from hotter objects to colder objects.

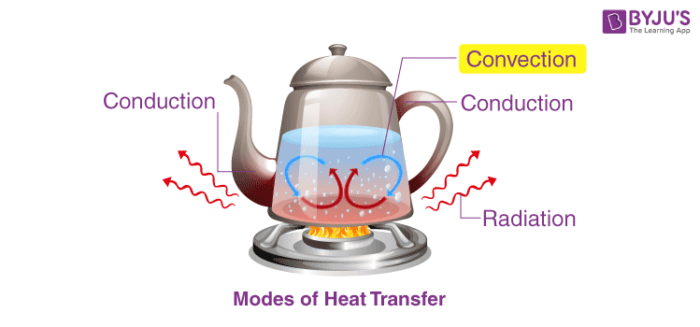
When there are objects which are at different temperatures or there is an object at a different temperature from the surroundings, then the transfer of heat takes place so that the object and the surrounding, both reach an equilibrium temperature.

There are three modes of heat transfer.

1. Conduction
2. Convection
3. Radiation

1. Conduction of Heat

Heat conduction is a process in which heat is transferred from the hotter part to the colder part in a body without involving any actual movement of the molecules of the body. Heat transfer takes place from one molecule to another molecule as a result of the vibratory motion of the molecules. Heat transfer through the process of conduction occurs in substances which are in direct contact with each other. It generally takes place in solids.

Conduction example: When frying vegetables in a pan. Heat transfer takes place from flame to the pan and then to the vegetables.

Based on the conductivity of heat, substances can be classified as conductors and insulators. Substances that conduct heat easily are known as conductors and those that do not conduct heat are known as insulators.

2. Convection of Heat

In this process, heat is transferred in the liquid and gases from a region of higher temperature to a region of lower temperature. Convection heat transfer occurs partly due to the actual movement of molecules or due to the mass transfer.

For example. Heating of milk in a pan.

3. Radiation of Heat

It is the process in which heat is transferred from one body to another body without involving the molecules of the medium. Radiation heat transfer does not depend on the medium.

For example: In a microwave, the substances are heated directly without any heating medium.

Recommended Videos

Factors Affecting Heat Transfer

Now we will discuss the rate of heat transfer or the factors on which it depends. The rate of heat transfer depends on the following:

ΔQΔt ∝ A(T1–T2)x

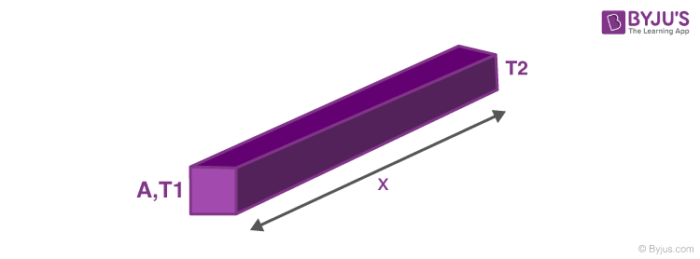
So the heat transfer equation comes out to be, ΔQΔt = K A(T1–T2)x where, K is the heat transfer coefficient. Here if heat flow is positive then we can infer T1 > T2. So heat flows from higher temperature to lower temperature. We can see that an analogy with electricity can be drawn, here temperature plays the role of potential difference and rate of heat transfer is like current while the rest of expression is like Electric Resistance. Now that we have drawn an analogy, so there must be series and parallel connections here also,

1. Heat Transfer in Series

Let the temperature of the junction be T. Therefore for the first rod,

⇒ ΔQΔt = K1 A1(T1–T)L1 —- (1)

Also for the second rod,

⇒ ΔQΔt = K2 A2(T–T2)L2 —- (2)

Since the temperature of conjunction remains constant, so the rate of heat transfer in (1) and (2) must be the same. Using the equation we can find the Value of temperature ‘T′.

2. Heat Transfer in Parallel

For rod 1,

ΔQΔt = K1A1(T1–T2)L —- (3)

For rod 2,

ΔQΔt = K2 A2(T1–T2)L —- (4)

So, net heat flow is the summation of (3) and (4). Suppose that the outside temperature is T and the depth of the lake is h. How much time will it take to freeze the entire lake? The latent heat of ice is L and thermal conductivity is K.

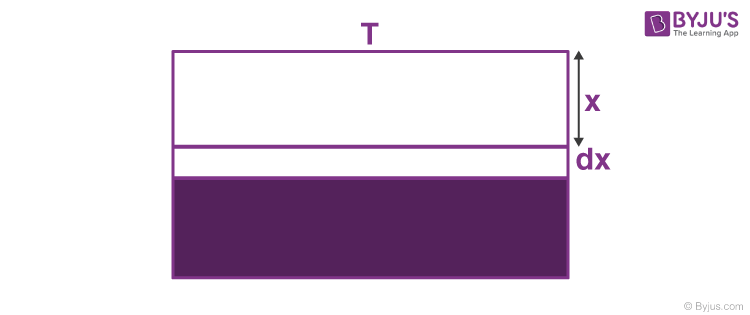
At this point, the rate of heat transfer is, ⇒ dQdt = KATx

⇒ dQ = KATx dt —- (5)

This heat is taken out and dx layer of ice is formed.

dm = ρA.dx —- (6)

Also,

dQ = dm.L

Putting values from (5) and (6) we get,

KATx dt = ρA.dx.L

⇒ ∫t0 dt = ρLKT∫h0x.dx

Integrating with limits we get,

t = ρLh22KT