Equivalent Resistance Formula

The equivalent resistance is where the aggregate resistance connected either in parallel or series is calculated. Essentially, the circuit is designed either in Series or Parallel. Electrical resistance shows how much energy one needs when you move the charges/current through your devices. If you require lots of energy, then the resistance necessary is also high. The equivalent resistance of a network is that single resistor that could replace the entire network in such a way that for a certain applied voltage V you get the same current I as you were getting for a network.

Equivalent resistance formula for series resistance is given by,

Equivalent resistance formula for parallel resistance is articulated as,

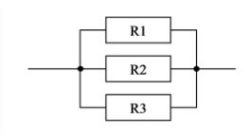
Where, R1, R2…..Rn the given resistors.

Equivalent Resistance Examples

Let’s see some examples of equivalent resistance numerical:

Solved Examples

Problem 1: What is the equivalent resistance if 3Ω, 20Ω and 32Ω are connected in series.
Answer:

Equivalent resistance in series is given by
R = R₁ + R₂ + …… + R_n
= 3 Ω + 20 Ω + 32 Ω
R  = 55 Ω.

Problem  2: What is the equivalent resistance if 34 Ω and 20 Ω are connected in parallel.
Answer:

Equivalent resistance in parallel is given by

Or

R_p = 12.66 Ω