Binding Energy

Binding energy is typically defined as the smallest amount of energy that is required to remove a particle from a system of particles. In other words, it is the energy that is used to separate a system of particles into single units. We study about binding energy mostly in atomic physics and chemistry as well as in condensed matter physics. In nuclear physics, the term binding energy is used to describe separation energy.

Binding energy is necessary to split subatomic particles in atomic nuclei or the nucleus of an atom into its components, namely: neutrons and protons or collectively known as nucleons. The binding energy of nuclei is a positive value because every nucleus needs net energy to isolate them into neutron and proton. Binding energy is also applicable to atoms and ions bound together in crystals.

Types of Binding Energy

Binding energy is of several types, and each operates over a different distance and energy scale. An important point to note here is that if the size of a bound system is small, then its associated binding energy will be higher. We will look at the types in brief below.

Electron Binding Energy – Ionization Energy

Electron binding energy, which is commonly known as ionization energy, is the energy required to remove an electron from its atomic orbital. The electron binding energy is mostly derived as a result of the electromagnetic interaction that occurs between the electron and the nucleus, the other electrons of the atom, molecule or solid that is usually mediated by photons.

Atomic Binding Energy

The atomic binding energy of the atom is the energy that is used to break down an atom into free electrons and a nucleus. We can say that it is the sum of the ionization energies of all the electrons that belong to a particular atom. The atomic binding energy is derived from the electromagnetic interaction between the electrons with the nucleus, which is mediated by the photons.

Nuclear Binding Energy

Nuclear binding energy is basically the energy required to dismantle a nucleus into free unbound neutrons and protons. It is the energy equivalent of the mass defect, the difference between the mass number of a nucleus and its measured mass. Nuclear binding energy is derived from the residual strong force or nuclear force, which again is mediated by 3 types of mesons.

Nuclear binding energy can be determined once the mass defect is calculated, usually by converting mass to energy by applying E = mc². When this energy is calculated, which is of joules for a nucleus, you can scale it into per-mole quantities and per-nucleon. You need to multiply by Avogadro’s number to convert into joules/mole and divide by the number of nucleons to convert to joules per nucleon.

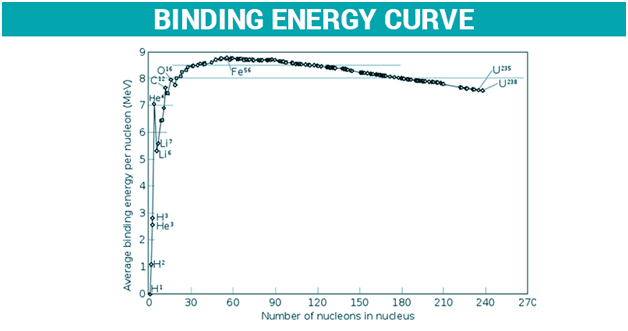
Nuclear binding energy is also applied to situations where the nucleus splits into fragments that consist of more than one nucleon, wherein the binding energies of the fragments can be either negative or positive based on the position of the parent nucleus on the nuclear binding energy curve. When heavy nuclei split or if the new binding energy is known when the light nuclei fuse, either of these processes results in the liberation of binding energy.

Mass Defect

The nuclear binding energy holds a significant difference between the nucleus’s actual mass and its expected mass depending on the sum of the masses of isolated components.

Hence, energy and mass are related based on the following equation:

Where c is the speed of light. In nuclei, the binding energy is so high that it holds a considerable amount of mass.

The actual mass is less than the sum of individual masses of the constituent neutrons and protons in every situation because energy is ejected when the nucleus is created. This energy consists of mass which is ejected from the total mass of the original components and is called a mass defect. This mass is missing in the final nucleus and describes the energy liberated when the nucleus is made.

Mass defect is determined as the difference between the atomic mass observed (Mo) and expected by the combined masses of its protons (mp, every proton has a mass of 1.00728 AMU) and neutrons (mn, 1.00867 AMU).

Bond Energy or Bond-dissociation Energy

We are talking about bond energy and bond-dissociation energy, which are basically measures of the binding energy between the atoms in a chemical bond. Bond energy is the energy that is used to disassemble a molecule into its constituent atoms. It appears in the form of chemical energy released during chemical explosions, the burning of chemical fuel and other processes.

Applications

Binding energy is also applied in determining whether fusion or fission will be favourable. For elements that are lighter than iron-56, the fusion releases energy since the nuclear binding energy rises with the hike in mass. Elements that are heavier than iron-56 release energy on fission since the lighter elements consist of higher binding energy. Hence, there exists a peak at iron-56 according to the nuclear binding energy curve.