Centre of Mass of Solid Hemisphere

There is a special point in a system or object, called the centre of mass that moves as if all of the mass of the system is concentrated at that point. The system will move as if an external force is applied to the object of mass M located at the centre of mass. In this article, we will determine the centre of mass of a solid hemisphere.

How to Find Centre of Mass of Solid Hemisphere

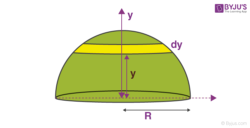
We are considering a solid hemisphere of mass M and has the radius R. The centre of mass will lie on the vertical line passing through the centre of the hemisphere, the vertical line is also the normal to the base. In order to find the centre of mass, we have to consider an element.

We are taking an elemental disc at a height h from the base of the hemisphere. The mass of the elemental disc is dM and the width is dy.

The radius of the disc is

Mass of the disc dM = (3M/2πR³) × (πr²dy)…..(2)

Substitute equa(1) in equa(2)

dM = (3M/2πR³) × π(R² – y²)dy)

Y-coordinate of Centre of mass,y_c = (1/M)ഽydM,

Here y is the y-coordinate which represents the height of the elemental disc from the base.

Putting the value of dM and calculating the centre of mass, we get

y_c= (1/M)ഽy(3M/2R³) × (R²-y²)dy)

Integrating between the limits 0⟶R

= (3/2R²)[(R⁴/2) – (R⁴/4)] = 3R/8

y_c = 3R/8

Centre of Mass of the solid hemisphere, y_c = 3R/8,

Here R is the radius of the hemisphere.

Centre of Mass and Collisions