The distance between two points is the length of the line joining the two points. If the two points lie on the same horizontal or same vertical line, the distance can be found by subtracting the coordinates that are not the same.
In analytic geometry, distance formula is used to find the distance measure between two lines, the sum of the lengths of all the sides of a polygon, perimeter of polygons on a coordinate plane, the area of polygons and many more. For example, we can find the lengths of the sides of a triangle using the distance formula and determine whether the triangle is scalene, isosceles or equilateral.
Table of Contents:
- How to Find the Distance between Two Points
- Distance Formula from Point to Line
- Distance between Parallel Lines
- Example Problems
How to Find the Distance between Two Points
The distance between two points of the xy-plane can be found using the distance formula. An ordered pair (x, y) represents co-ordinate of the point, where x-coordinate (or abscissa) is the distance of the point from the x-axis and y-coordinate (or ordinate) is the distance of the point from the y-axis.
Formula to find Distance between Two Points in 2d plane:
Consider two points A(x1,y1) and B(x2,y2) on the given coordinate axis. The distance between two points formula is given as:
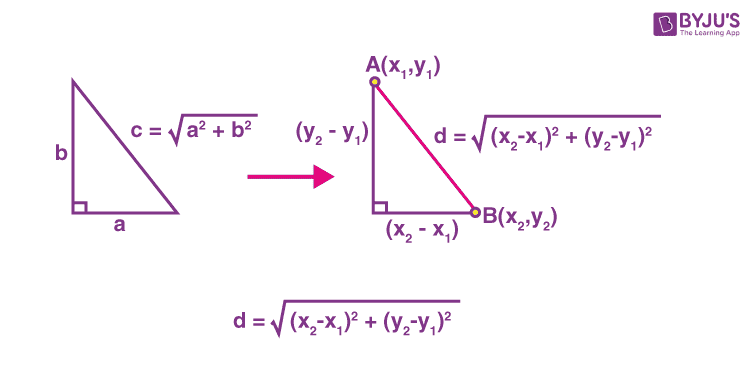
Formula to find Distance between Two Points in 3d plane:
The below formula is used to find the distance between two points, Let P(x1, y1, z1) and Q(x2, y2, z2) are the two points in three dimensions plane.
So,
Distance Formula from Point to Line

Consider Ax + By + C = 0 be an equation of line and P be any point in the cartesian-coordinate plane having coordinates P(x1, y1).
The distance formula from a point to line is as given below:
Distance between Two Parallel Lines
The distance between parallel lines is the shortest distance from any point on one of the lines to the other line.
Also defined as, The distance between two parallel lines = Perpendicular distance between them.
Consider two parallel lines, y = mx + c1 and y = mx + c2
Let d be the distance between both the lines.

Formula to find the shortest distance between two non-intersecting lines is as given below:
Distance between Two Points in Polar Co-ordinates
Let O be the pole and OX be the initial line. Let P and Q be two given points whose polar coordinates are (r1, θ1) and (r2, θ2), respectively. Then the distance between two points formula is given by,
where θ1 and θ2 in radians.
Example Problems
Example 1: Find the distance between P(3, -4) and Q(-5, -1).
Solution:
Applying distance formula:
= √(64 + 9)
= √73 or 8.54 (approx)
Example 2: Find the distance between the parallel lines -3x + 10y + 5 = 0 and -3x + 10y + 10 = 0.
Solution:
Comparing the given equation with the general equation of parallel lines Ax + By + C1 = 0 and Ax + By + C2 = 0, we get
Here, A = -3, B = 10, C1 = 5 and C2 = 10.
Applying formula:
The required distance is, d = |10–5|/√(-32+102) = 5/√109.
Example 3: Find the distance of line 2x + 3y – 13 = 0 from the point (1, –2).
Solution:
Given line is 2x + 3y – 13 = 0
Let d be the required distance.
Comparing the given equation with the general equation of line Ax + By + C = 0, we get
A = 2, B = 3 and C = –13
We know, the formula to find the distance between a point and a line is
Given point is (x1, y1) = (1, –2).
Therefore, d = |2(1) + 3(-2) + (-13)|/√(22+32) = 17/√13.
Example 4: Find the equations of the straight lines parallel to 5x – 12y + 26 = 0 and at a distance of 4 units from it.
Solution: Given lines is 5x – 12y + 26 = 0
Equations of any line parallel to given equation is 5x – 12y + m = 0
Distance between both the lines is 4 units (given)
Now,
|m-26|/√(25+144) = 4
⇒ ± (m – 26) = 52
or m = -26, 78
Required equations of lines are: 5x – 12y – 26 = 0 and 5x – 12y + 78 = 0
Example 5: If the distance between the points (a, 2) and (3, 4) be 8, then find the value of a.
Solution:
Example 6: The distance between the points
Solution:
Example 7: The distance of the middle point of the line joining the points (a sin θ, 0) and (0, a cosθ) from the origin is _______.
Solution: Mid-point will be
Related Video:


Comments