Below we discussed have some of the most frequently asked questions about Bernoulli’s principle and students will also find answers to these questions.

Important Questions on Bernoulli’s Principle

1. What is Bernoulli’s Principle?

Ans: Bernoulli’s principle is based on the principle of conservation of energy. According to Bernoulli’s principle, In fluid dynamics, for a non-viscous, incompressible, non – conducting fluid, an increase in the velocity of the fluid during its flow (laminar), results in a simultaneous decrease in pressure (or potential energy) of the fluid. The converse of this is also true.

2. What is Bernoulli’s Equation?

Ans: Bernoulli’s equation is based on Bernoulli’s Principle for fluid flow. According to Bernoulli’s equation for a fluid, we can see that the total energy of the system is always constant. It is expressed as per the relation, which is given below.

\begin{array}{l} P + \frac{1}{2} ρ v^{2} + ρ g h = constant for a system \end{array}

where,

P is the Pressure Energy,

\begin{array}{l} \frac{1}{2} ρ v^{2} is the Kinetic Energy of the system per unit volume, \end{array}

\begin{array}{l} ρ g h is the Potential Energy per unit volume . \end{array}

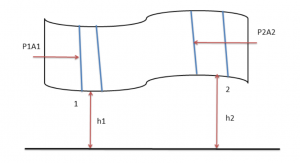
Suppose there is an irrotational and steady flow of an incompressible and non-viscous liquid as shown in the figure below. There is a tube of varying cross section and varying height. Consider a liquid contained between the cross sections 1 and 2 of the tube. The heights of 1 and 2 are h1 and h2, respectively from a reference level. This liquid advances into the tube and after a time t is contained between the cross sections 1 and 2.

\begin{array}{l} P_{1} + \frac{1}{2} p v_{1}^{2} + ρ g h_{1} = P_{2} + \frac{1}{2} ρ v_{2}^{2} + ρ g h_{2} \end{array}

\begin{array}{l} P + \frac{1}{2} ρ v^{2} + ρ g h = constant for a system \end{array}

3. Water flows in a horizontal tube as shown in the figure below. The pressure of water changes by 600 N/m² between A and B, where the areas of cross section are 30 cm² and 15 cm², respectively. Find the rate of flow of water through the tube.

Bernoullis Principle

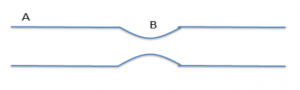
Ans:

\begin{array}{l} Let the velocity at A = v_{A} \end{array}

\begin{array}{l} and the velocity at B = v_{B} \end{array}

From the equation of continuity

\begin{array}{l} \frac{v_{B}}{v_{A}} = \frac{30 c m^{2}}{15 c m^{2}} = 2 \dots . . (1) \end{array}

Applying Bernoulli equation,

\begin{array}{l} P_{A} + \frac{1}{2} v_{A}^{2} = P_{B} + \frac{1}{2} ρ v_{B}^{2} \end{array}

\begin{array}{l} P_{A} - P_{B} = \frac{1}{2} ρ (v_{B}^{2} - v_{A}^{2}) \end{array}

Using equation (1),

\begin{array}{l} P_{A} - P_{B} = \frac{3}{2} ρ (v_{A}^{2}) \end{array}

and we know that,

\begin{array}{l} P_{A} - P_{B} = 600 N / m^{2} \end{array}

Putting this value we get

\begin{array}{l} v_{A} = 0.63 m / s \end{array}

\begin{array}{l} \Rightarrow v_{A} = 63 c m / s \end{array}

Therefore rate of flow = (30 cm²) (63 m/s) = 1890 cm³/s

4) What are some of the best books to refer for Bernoulli’ Equation in physics?

Ans. – Regarding books for JEE preparation, Concepts of Physics by H. C. Verma is definitely one of the best books. Apart from that, books by Arihant Publication also have good practice problems.

To know more about different topics in physics join us here at BYJU’S.

For more application based learning, check out BYJU’S – The Learning App! Keep Learning!

Important Questions on Bernoulli’s Principle

Comments

Leave a Comment Cancel reply