Frequency deviation in FM is

Change in carrier frequency to the frequency above and below the centre frequency

The variation of the instantaneous carrier frequency in proportion to the modulating signal

Amplitude limiter in FM receivers are used to

Remove amplitude variations due to noise

Frequency Modulation - Definition, Applications, Advantages, Equation

Frequency modulation or commonly referred to as FM is a common term that we hear in our daily lives. Today, FM is used widely in radio communication and broadcasting. But have we wondered what it actually is or what is the technology and mechanism behind it? We will try to understand what frequency modulation is in this lesson and also learn its mechanism as well as its applications.

Table of Content

What is Frequency Modulation?
Frequency Modulation Equations
Expression for Frequency Modulated Wave
Frequencies in Frequency Modulation
Modulation Index
Graphical Representation of Frequency Modulated Wave
Frequency Demodulation
Advantages and Disadvantages of Frequency Modulation

What is Frequency Modulation?

Frequency modulation is a technique or a process of encoding information on a particular signal (analogue or digital) by varying the carrier wave frequency in accordance with the frequency of the modulating signal. As we know, a modulating signal is nothing but information or message that has to be transmitted after being converted into an electronic signal.

Much like in amplitude modulation, frequency modulation also has a similar approach where a carrier signal is modulated by the input signal. However, in the case of FM, the amplitude of the modulated signal is kept or it remains constant.

If we talk about the applications of frequency modulation, it is mostly used in radio broadcasting. It offers a great advantage in radio transmission as it has a larger signal-to-noise ratio. Meaning, it results in low radio frequency interference. This is the main reason that many radio stations use FM to broadcast music over the radio.

Additionally, some of its uses are also found in radar, telemetry, seismic prospecting and in EEG, different radio systems, music synthesis as well as in video-transmission instruments.

Frequency Modulation Equations

Frequency modulation equations mainly consist of a sinusoidal expression with the integral of the baseband signal that can be either a sine or cosine function.

It can be represented mathematically as;

m(t) = A_m cos (ω_mt + Ɵ) ……………… 1

m(t) → modulating signal

Where,

A_m → Amplitude of the modulating signal.

ω_m → Angular frequency of the modulating signal.

Ɵ → is the phase of the modulating signal.

Such as amplitude modulation, when we try to modulate an input signal (information), we need a carrier wave, we will experience

C(t) = A_c cos (ω_ct + Ɵ) ………….. 2

Angular modulation, which means ω_c (or) Ɵ of the carrier wave starts varying linearly with respect to the modulating signal like amplitude modulation.

Also Read: Communication Systems

Case I: Any Instant

Modulating signal at any instant of time.

Modulating signal at any instant of time

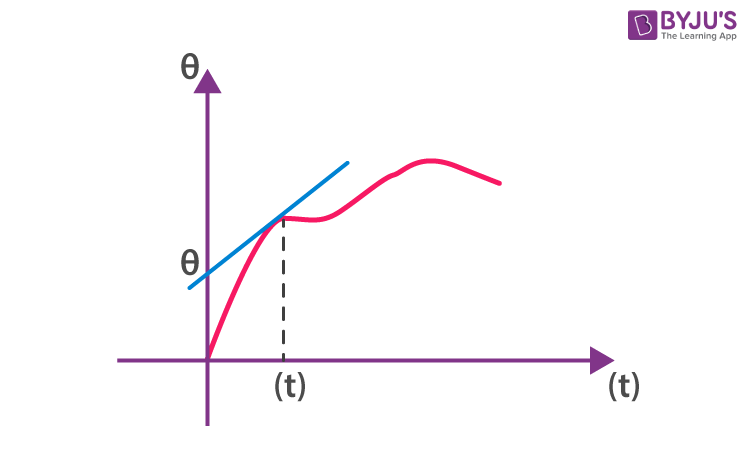
C(t) = A_c cos (ω_ct + Ɵ)

For any particular instant (ω_ct + Ɵ) is not varying with respect to time the Ɵ becomes so it Ɵ₀ = constant, then

ω_c = also constant

If we draw a tangent for the given signal at any instant of time, the slope of the tangent gives ω_cand the tangent when it cuts the Ɵ-axis gives Ɵ₀ value.

Case II: For a Small Interval of Time

Now let us consider a small interval of time Δt = t₂ – t₁

Time interval, t₁ < t < t₂, we will look this into two particular instant of t₁ and t₂

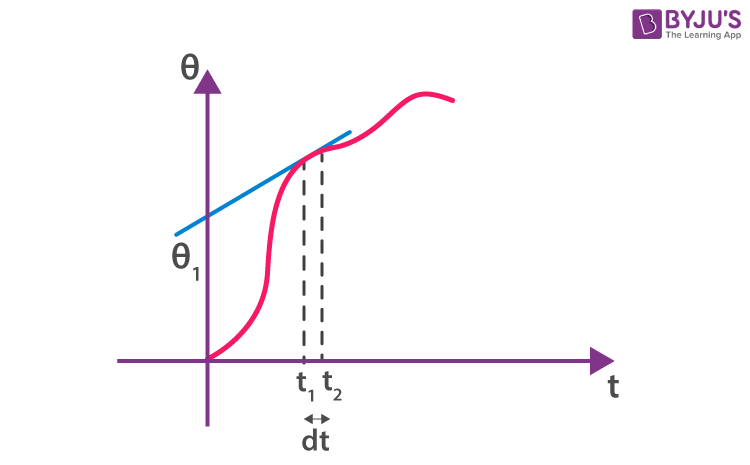
Modulating signal at small interval of time

Let us consider an instant at (t₁), if we draw a tangent to given signal at (t₁), the slope of curve instantaneous frequency (w_i) at that particular instant

Similarly, intercept of the tangent with Ɵ – axis gives the instantaneous phase (Ɵ_i). Likewise, we can get w_i for any instant of the given curve. From this one thing is clear.

{{\omega }_{i}}=\frac{d\theta }{dt}

Ɵ – is the phase at the instant

We write this as a function of time (t), instantaneous frequency is

\omega (t)=\frac{d\theta (t)}{dt}…………..3

\int\limits_{-\infty }^{t}{\omega (t)dt=\theta \,……………….\,4}

Equation 3 and 4 gives the fundamental understanding of phase and frequency. If we try to modulate this signal, let us see what’s happening at any instant of time the signal phase is

\theta (t)={{\omega }_{c}}t\int\limits_{-\infty }^{t}{k\,m(t)…………..(5)}

[this is known as phase modulation]

Where,

k – constant

ω_c → frequency of the carrier wave

m(t) → modulating signal

The insert signal in this phase becomes,

A cos Ɵ (t) = A_ccos [ω_ct + k m(t)]

If we need frequency of the wave,

\omega (t)=\frac{d\theta (t)}{dt}=

ω_c + km(t) ……….6 [this is known frequency modulation]

Where,

\overset{\bullet }{\mathop{m}}\,(t)=\frac{d}{dt}m(t)

As we know, the idea of frequency modulation, the frequency of the carrier wave must vary linearly with respect to particular signal as we can see it equation no 5. From this we get,

ω(t) = ω_c+ km(t)

If we do phase modulation it is nothing but a frequency modulation. When we do frequency modulation, we are differentiating the particular modulating signal which then automatically depicts it as phase modulation.

Expression for Frequency Modulated Wave

As we know from amplitude modulation, we need two sine (or) cosine waves for modulation.

m(t) = A_m cos (ω_mt) and

c(t) = A_c cos (ω_ct)

m(t) = A_m cos (2π f_mt)

c(t) = A_c cos (2πf_ct)

Then frequency modulated wave will be;

f_m(t) = f_c + k A_m cos (2π f_m t )

f_m (t) = f_c + k m(t)

Where,

fm(t) = is frequency modulated wave

f_c → frequency of the carrier wave

m(t) → modulating signal

k → proportionality constant.

Frequencies in Frequency Modulation

In FM, variation (or) deviation in frequency the maximum deviation Δf_max

Δf_{max = │}f_m(t)_–f_c│

_=│KA_m cos(2π f_mt)_│

The maximum deviation in frequency is K A_m

Generally, frequency deviation is defined as the measure of the change in a carrier frequency produced by the amplitude of the input modulating signal.

Modulation Index (μ)

Is the ratio of maximum deviation in frequency of the modulating signal.

\mu =\frac{\Delta {{f}_{\max }}}{{{f}_{m}}}=\frac{{{K}_{{{A}_{m}}}}}{{{f}_{m}}}

Also Read: Differences Between AM and FM

Graphical Representation of Frequency Modulated Wave

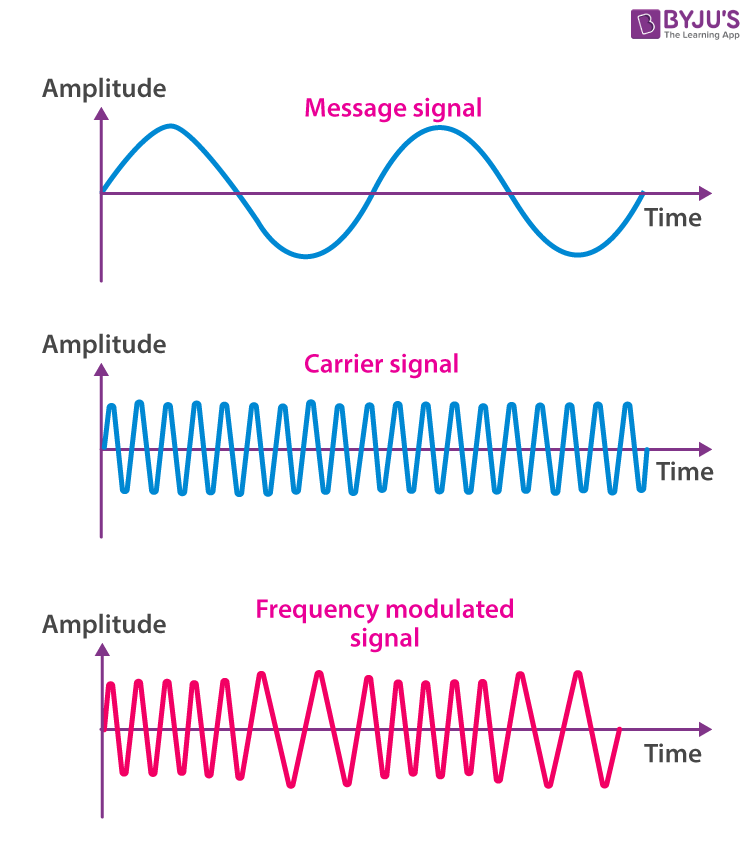
If we observe the graph, we will notice that the frequency of a carrier increases when the amplitude of the input signal is increased. Here, the carrier frequency is maximum when the input signal is at its highest. Meanwhile, the frequency of a carrier decreases if the amplitude of the modulating signal goes down. What it means is that the carrier frequency is minimum when the input signal is at its lowest.

Frequency Demodulation

When there is modulation, usually we need to successfully demodulate it and at the same time recover the original signal. In such cases, FM demodulator also known as FM discriminator or FM detector is used. While there are several types of FM demodulator, the main functionality of these devices is to convert the frequency variations of the input signal into amplitude variations of the output signal. The demodulators are used along with an audio amplifier, or possibly a digital interface.

Advantages and Disadvantages of Frequency Modulation

Advantages	Disadvantages
Less interference and noise.	Equipment cost is higher. Has a large bandwidth.
Power Consumption is less as compared to AM.	More complicated receiver and transmitter
Adjacent FM channels are separated by guard bands.	The antennas for FM systems should be kept close for better communication.