The geometrical representation of a complex number is one of the fundamental laws of algebra. A complex number z = α + iβ can be denoted as a point P(α, β) in a plane called Argand plane, where α is the real part, and β is an imaginary part
\(\begin{array}{l}\text{The value of i} = \sqrt{-1}\end{array} \)
.
In this article, students will learn the representation of Z modulus on the Argand plane, polar form, section formula and many more. Solved examples and clear diagrams will help them have a good understanding of the topic.
Table of Contents
Representation of Z Modulus on Argand Plane
Argand plane consists of the real axis (x-axis) and an imaginary axis (y-axis).
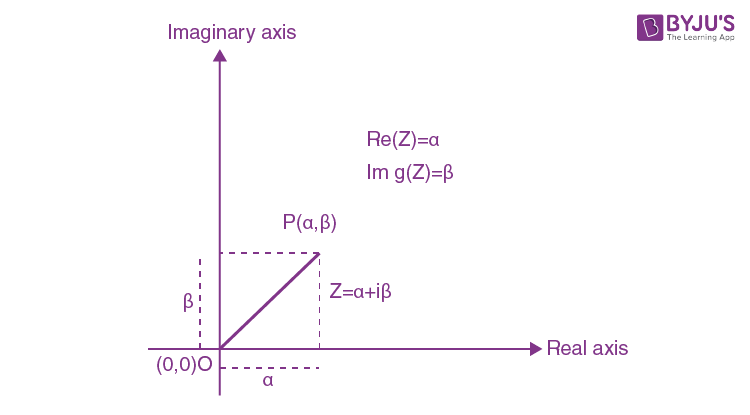
\(\begin{array}{l}\left| Z \right|=\sqrt{{{\left( \alpha -0 \right)}^{2}}+{{\left( \beta -0 \right)}^{2}}}\end{array} \)
\(\begin{array}{l}=\sqrt{{{\alpha }^{2}}+{{\beta }^{2}}}\end{array} \)
\(\begin{array}{l}=\sqrt{Re(z)^2 + Img(z)^2}\end{array} \)
\(\begin{array}{l}\left| z \right|=\left| \alpha +i\beta \right|=\sqrt{{{\alpha }^{2}}+{{\beta }^{2}}}\end{array} \)
Conjugate of Complex Numbers on Argand Plane
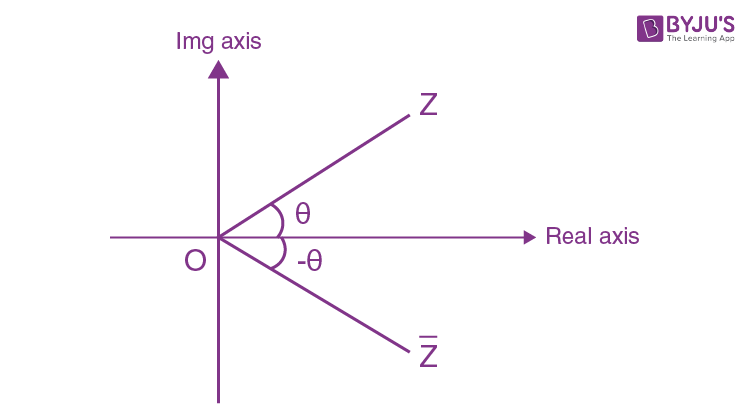
A conjugate of a complex number is a number with the same real part and opposite sign of the imaginary part but equal in magnitude.
Let Z = α + iβ be the complex number.
The mirror image of Z = α + iβ along the real axis will represent the conjugate of the given complex number.
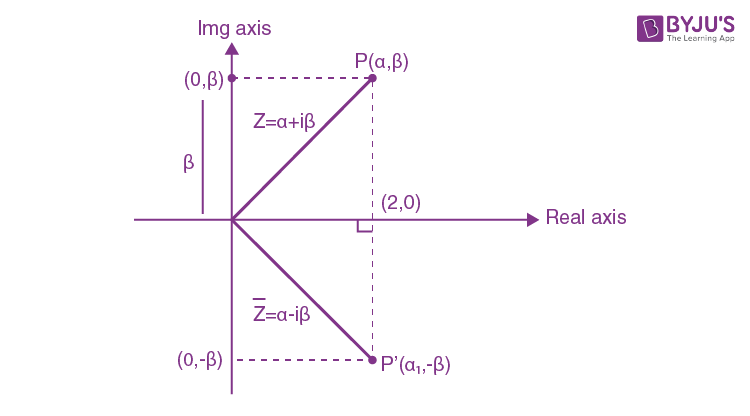
\(\begin{array}{l}Z=\alpha +i\beta\end{array} \)
(complex number)
\(\begin{array}{l}\overline{Z}=\alpha -i\beta\end{array} \)
(conjugate of complex number)
Distance between Two Points in Complex Plane
If two complex numbers Z1 and Z2 are denoted as P and Q, respectively, in the Argand plane, then the distance between P and Q will be given as,
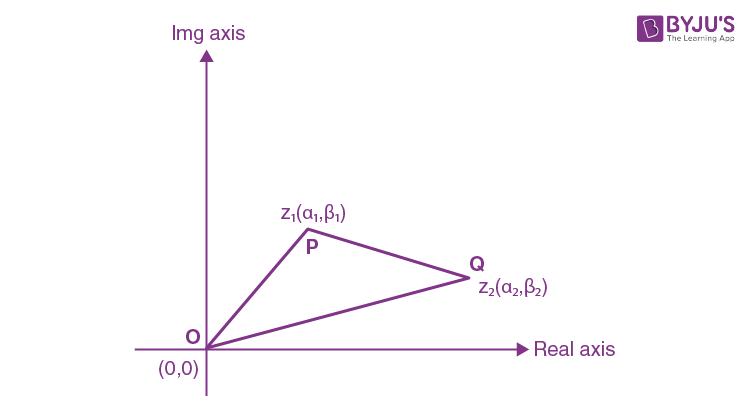
\(\begin{array}{l}PQ=\left| {{z}_{2}}-{{z}_{1}} \right|\end{array} \)
\(\begin{array}{l}=\left| \left( {{\alpha }_{2}}-{{\alpha }_{1}} \right)+i\left( {{\beta }_{2}}-{{\beta }_{1}} \right) \right|\end{array} \)
\(\begin{array}{l}=\sqrt{{{\left( {{\alpha }_{2}}-{{\alpha }_{1}} \right)}^{2}}+{{\left( {{\beta }_{2}}-{{\beta }_{1}} \right)}^{2}}}\end{array} \)
For example, find the distance of a point P, Z = (3 + 4i) from the origin.
Solution:
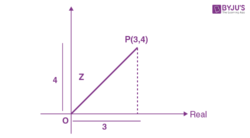
|Z| = |3 + 4i|
\(\begin{array}{l}=\sqrt{{{3}^{2}}+{{4}^{2}}}\end{array} \)
= 5 units
=> Also Read
Polar Form of Complex Number
Complex numbers can be represented in both rectangular and polar coordinates. Here, we will study the polar form of any complex number.
\(\begin{array}{l}Z=\left( \alpha +i\beta \right)\end{array} \)
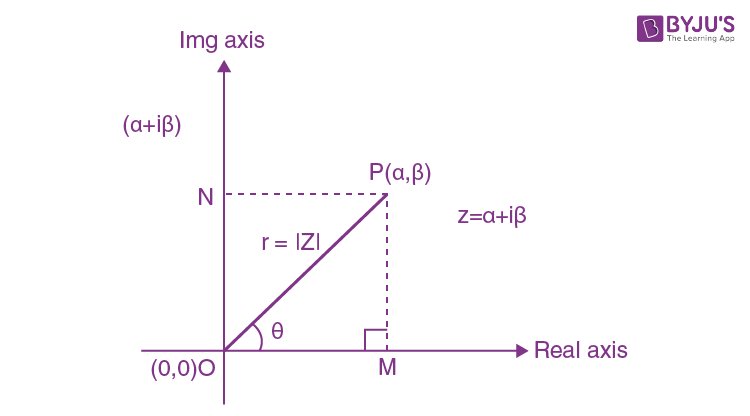
Let ‘θ’ be the angle between ‘OP’ and the real axis.
\(\begin{array}{l}Z=\alpha +i\beta ,\,\,\,\left| z \right|=r\end{array} \)
OM = r cos θ = α
ON = r sin θ = β
Hence,
\(\begin{array}{l}Z=\alpha +i\beta\end{array} \)
= (OM) + i (ON)
\(\begin{array}{l}=r\cos \theta +i\,\,r\sin \theta\end{array} \)
\(\begin{array}{l}=r\left( \cos \theta +i\,\,\sin \theta \right)\end{array} \)
\(\begin{array}{l}r=\sqrt{{{\alpha }^{2}}+{{\beta }^{2}}}=\left| z \right|=\left| \alpha +i\beta \right|\end{array} \)
Where ‘θ’ is called the argument of a complex number.
\(\begin{array}{l}\theta =\arg \left( z \right)\end{array} \)
For conjugate of a complex number,
\(\begin{array}{l}\arg \left( \overline{z} \right)=-\theta\end{array} \)
Algebra of Complex Numbers
Let’s discuss the different algebras of complex numbers. We mainly deal with addition, subtraction, multiplication and division of complex numbers.
Product of two complex numbers
\(\begin{array}{l}{{Z}_{1}}=\left( {{\alpha }_{1}}+i{{\beta }_{1}} \right)\end{array} \)
and
\(\begin{array}{l}{{Z}_{2}}=\left( {{\alpha }_{2}}+i{{\beta }_{2}} \right)\end{array} \)
in argand plane
\(\begin{array}{l}{{\theta }_{1}}=\arg \left( {{z}_{1}} \right)\end{array} \)
,
\(\begin{array}{l}{{\theta }_{2}}=\arg \left( {{z}_{2}} \right)\end{array} \)
(given)
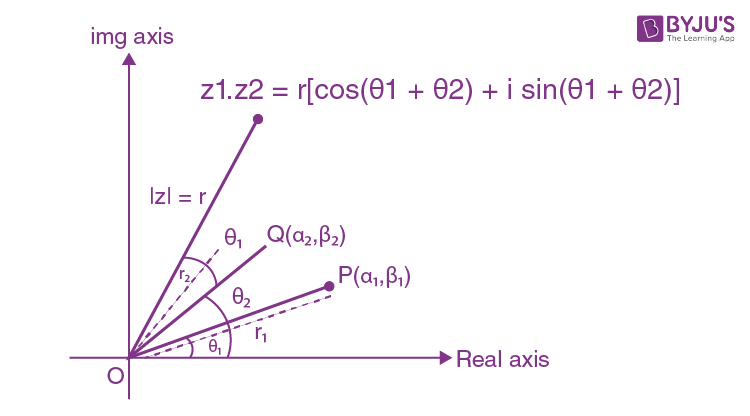
Now, on multiplying Z1 Z2 = Z
\(\begin{array}{l}Z=\left( {{\alpha }_{1}}+i{{\beta }_{1}} \right).\left( {{\alpha }_{2}}+i{{\beta }_{2}} \right)\end{array} \)
\(\begin{array}{l}={{r}_{1}}\left( \cos {{\theta }_{1}}+i\sin {{\theta }_{1}} \right).\,{{r}_{2}}\left( \cos {{\theta }_{2}}+i\,\sin {{\theta }_{2}} \right)\end{array} \)
\(\begin{array}{l}={{r}_{1}}{{r}_{2}}\left[ \cos \left( {{\theta }_{1}}+{{\theta }_{2}} \right)+i\,\sin \left( {{\theta }_{1}}+{{\theta }_{2}} \right) \right]\end{array} \)
Let say
\(\begin{array}{l}{{r}_{1}}.\,{{r}_{2}}=r\end{array} \)
.
\(\begin{array}{l}Z=r\left( \cos \left( {{\theta }_{1}}+{{\theta }_{2}} \right)+i\,\sin \left( {{\theta }_{1}}+{{\theta }_{2}} \right) \right)\end{array} \)
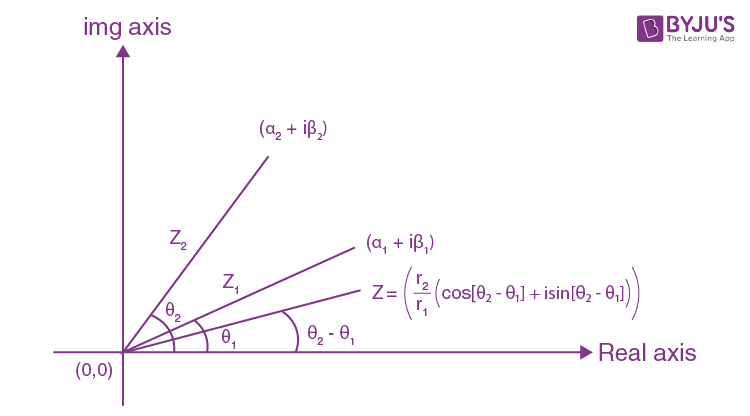
Division of two complex number
Let
\(\begin{array}{l}{{Z}_{1}}={{\alpha }_{1}}+i{{\beta }_{1}}={{r}_{1}}\left( \cos {{\theta }_{1}}+i\,\sin {{\theta }_{1}} \right)\end{array} \)
\(\begin{array}{l}{{Z}_{2}}={{\alpha }_{2}}+i{{\beta }_{2}}={{r}_{2}}\left( \cos {{\theta }_{2}}+i\,\sin {{\theta }_{2}} \right)\end{array} \)
Where,
\(\begin{array}{l}{{\theta }_{1}}=\arg \left( {{Z}_{1}} \right)\end{array} \)
\(\begin{array}{l}{{\theta }_{2}}=\arg \left( {{Z}_{2}} \right)\end{array} \)
Now, Z represents a complex number
\(\begin{array}{l}Z=\frac{{{Z}_{2}}}{{{Z}_{1}}}={{Z}_{2}}Z_{1}^{-1}\end{array} \)
\(\begin{array}{l}Z={{Z}_{2}}Z_{1}^{-1}=\frac{{{Z}_{2}}\overline{{{Z}_{1}}}}{{{\left| Z \right|}^{2}}}\end{array} \)
\(\begin{array}{l}=\frac{{{r}_{2}}}{{{r}_{1}}}\left( \cos \left( {{\theta }_{2}}-{{\theta }_{1}} \right)+i\,\sin \left( {{\theta }_{2}}-{{\theta }_{1}} \right) \right)\end{array} \)
Note:
1. On the multiplication of two complex numbers, their argument is added.
\(\begin{array}{l}\theta ={{\theta }_{1}}+{{\theta }_{2}}\end{array} \)
2. On the division of two complex numbers, their argument is subtracted.
\(\begin{array}{l}\theta ={{\theta }_{1}}-{{\theta }_{2}}\end{array} \)
Equation of Straight Line Passing through Two Complex Points
In Algebra, we have studied that the equation of the straight line passing through two points (x1, y1) and (x2, y2) is
\(\begin{array}{l}y-{{y}_{1}}=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right)\end{array} \)
In complex numbers
Equation of straight line passes through two points A(Z1), and B(Z2) can be represented as,
\(\begin{array}{l}Z-{{Z}_{1}}=\frac{{{Z}_{2}}-{{Z}_{1}}}{\overline{{{Z}_{2}}}-\overline{{{Z}_{1}}}}\left( \overline{Z}-\overline{{{Z}_{1}}} \right)\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{Z-{{Z}_{1}}}{{{Z}_{2}}-{{Z}_{1}}}=\frac{\overline{Z}-\overline{{{Z}_{1}}}}{\overline{{{Z}_{2}}}-\overline{{{Z}_{1}}}}\end{array} \)
\(\begin{array}{l}\text{Where}\ \overline{Z}\ \text{represent conjugate of Z}.\end{array} \)
Or
\(\begin{array}{l}\left| \begin{matrix} Z & \overline{Z} & 1 \\ {{Z}_{1}} & \overline{{{Z}_{1}}} & 1 \\ {{Z}_{2}} & \overline{{{Z}_{2}}} & 1 \\ \end{matrix} \right|=0\end{array} \)
Which is the required equation of the straight line.
Section Formula in Complex Numbers
Let A(Z1), B(Z2) and C(Z) be the three points on a line.
If C divides line AB (internally) in the ratio of m : n, so that
\(\begin{array}{l}\frac{AC}{BC}=\frac{m}{n}\end{array} \)
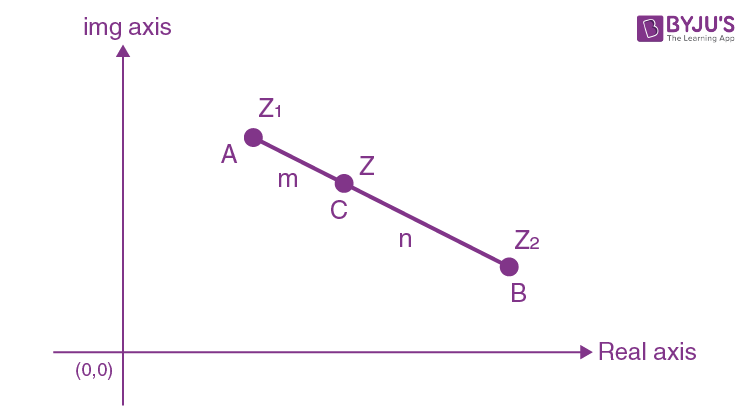
Then,
\(\begin{array}{l}Z=\frac{m\,{{Z}_{2}}+n\,{{Z}_{1}}}{m+n}\end{array} \)
Co-linearity condition
Let Z1, Z2 and Z3 be the three points A(Z1), B(Z2) and C(Z3).
So, the condition for collinearity will be,
|AB| + |BC| = |AC|
Or,
\(\begin{array}{l}\left| \begin{matrix} {{Z}_{1}} & \overline{{{Z}_{1}}} & 1 \\ {{Z}_{2}} & \overline{{{Z}_{2}}} & 1 \\ {{Z}_{3}} & \overline{{{Z}_{3}}} & 1 \\ \end{matrix} \right|=0\end{array} \)
Equation of Circle in Complex Plane
Equation of circle, whose centre is the point representing the complex number Z0 and radius is ‘r’.
Equation of circle will be
\(\begin{array}{l}\left| Z-{{Z}_{0}} \right|=r\end{array} \)
.
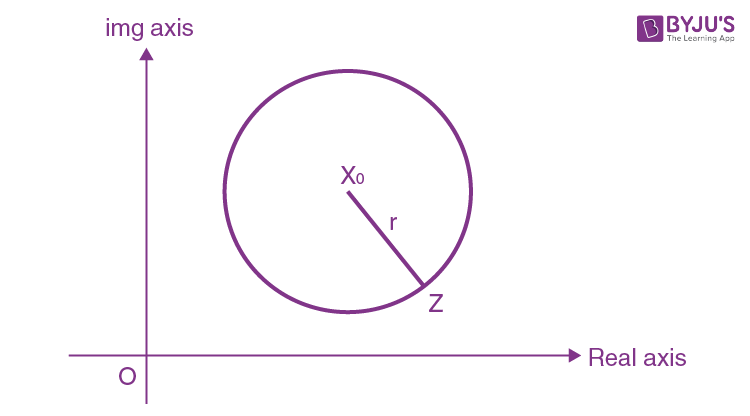
Equation of circle if Z1 and Z2 be the diametric end points of the circle,
\(\begin{array}{l}\left( Z-{{Z}_{1}} \right)\left( \overline{Z}-\overline{{{Z}_{2}}} \right)+\left( Z-{{Z}_{2}} \right)\left( \overline{Z}-\overline{{{Z}_{1}}} \right)=0\end{array} \)
Solved Examples
Example 1: Find the length of the line segment joining the points −1−i and 2+3i.
Solution:
Since the coordinates in the complex plane are (2, 3) and (−1,−1), the required distance is 5.
We know that the distance between z1 and z2 is |z1−z2|. Therefore, the required length is |2+3i+1+i|=5.
Example 2: Let the complex numbers z1, z2 and z3 be the vertices of an equilateral triangle. Let z0 be the circumcentre of the triangle, then z12 + z22 + z32 is equal to
Solution:
Let r be the circumradius of the equilateral triangle and ω the cube root of unity.
Let ABC be the equilateral triangle with z1, z2 and z3 as its vertices A, B and C, respectively, with circumcentre O'(z0).
\(\begin{array}{l}\text{The vectors}\ {O}’A,{O}’B,{O}’C\ \text{are equal and parallel to}\ O{A}’,O{B}’,O{C}’,\ \text{respectively}.\end{array} \)
Then the vectors, \(\begin{array}{l}\overrightarrow{O{A}’}={{z}_{1}}-{{z}_{0}}=r{{e}^{i\theta }}\\ \overrightarrow{O{B}’}={{z}_{2}}-{{z}_{0}}=r{{e}^{\left(\theta +\frac{2\pi }{3} \right)}}=r\omega {{e}^{i\theta }} \\\overrightarrow{O{C}’}={{z}_{3}}-{{z}_{0}}=r{{e}^{i\,\left(\theta +\frac{4\pi }{3} \right)}}\\=r{{\omega }^{2}}{{e}^{i\theta }} \\\ {{z}_{1}}={{z}_{0}}+r{{e}^{i\theta }},{{z}_{2}}={{z}_{0}}+r\omega {{e}^{i\theta }},{{z}_{3}}={{z}_{0}}+r{{\omega }^{2}}{{e}^{i\theta }} \\z_{1}^{2}+z_{2}^{2}+z_{3}^{2}=3z_{0}^{2}+2(1+\omega +{{\omega }^{2}}){{z}_{0}}r{{e}^{i\theta }}+ (1+{{\omega }^{2}}+{{\omega }^{4}}){{r}^{2}}{{e}^{i2\theta }}\\ =3z_{^{0}}^{2},\end{array} \)
Since
\(\begin{array}{l}1+\omega +{{\omega }^{2}}=0=1+{{\omega }^{2}}+{{\omega }^{4}}\end{array} \)
.
Example 3: If the centre of a regular hexagon is at the origin and one of the vertexes on the Argand diagram is 1 + 2i, then find its perimeter.
Solution:
Let the vertices be z0, z1,.., z5 with respect to centre O at origin and |z0|= √5.
\(\begin{array}{l}\Rightarrow {{A}_{0}}{{A}_{1}}= |{{z}_{1}}-{{z}_{0}}|\,=\,|{{z}_{0}}{{e}^{i\,\theta }}-{{z}_{o}}| \\= |{{z}_{0}}||\cos \theta +i\sin \theta -1| \\=\sqrt{5}\,\sqrt{{{(\cos \theta -1)}^{2}}+{{\sin }^{2}}\theta } \\=\sqrt{5}\,\sqrt{2\,(1-\cos \theta )}\\=\sqrt{5}\,\,2\sin (\theta /2) \\{{A}_{0}}{{A}_{1}}=\sqrt{5}\,.\,2\sin \,\left(\frac{\pi }{6} \right)=\sqrt{5}\left( \text because \,\,\theta =\frac{2\pi }{6}=\frac{\pi }{3} \right)\end{array} \)
Similarly,
\(\begin{array}{l}{{A}_{1}}{{A}_{2}}={{A}_{2}}{{A}_{3}}={{A}_{3}}{{A}_{4}}={{A}_{4}}{{A}_{5}}={{A}_{5}}{{A}_{0}}=\sqrt{5}\end{array} \)
Hence the perimeter of, regular polygon is
\(\begin{array}{l}={{A}_{o}}{{A}_{1}}+{{A}_{1}}{{A}_{2}}+{{A}_{2}}{{A}_{3}}+{{A}_{3}}{{A}_{4}}+{{A}_{4}}{{A}_{5}}+{{A}_{5}}{{A}_{0}}\\=\,\,6\sqrt{5}\end{array} \)
Complex Numbers JEE Main Important Topics
Complex Numbers JEE Main Important Questions
Complex Numbers JEE Previous Year Questions
Frequently Asked Questions
Q1
What do you mean by the conjugate of a complex number?
If z = x+iy, then the conjugate of z is denoted by z̄ = x-iy. Conjugate will have the same real part and imaginary part with opposite signs but equal in magnitude.
Q2
Give the formula to find the distance between two points in the complex plane.
If two complex numbers are denoted as P(α1, β1) and Q(α2, β2), respectively, in the Argand plane, then the distance between P and Q is given by PQ = √[(α2-α1)2 + (β2– β1)2].
Q3
How do you represent a complex number in polar form?
Let z = x+iy be the complex number. Then we use the formula x = r sin θ, y = r cos θ. We find r by using r = √(x2+y2). θ = tan-1(y/x).
In polar form z = r cos θ + i sin θ.














Comments