I.E. Irodov Solutions on Interference of Light

1. Demonstrate that when two harmonic oscillations are added, the time-averaged energy of the resultant oscillation is equal to the sum of the energies of the constituent oscillations, if both of them

(a) have the same direction and are incoherent, and all the values of the phase difference between the oscillations are equally probable;

(b) are mutually perpendicular, have the same frequency, and an arbitrary phase difference.

(a) In this case the net vibration is given by

x = a₁ cos ωt + a₂ cos(ωt + δ)

Where δ is the phase difference between the two vibrations which varies rapidly and randomly in the interval (0, 2π). (This is what is meant by incoherence). Then

x = (a₁ + a₂ cos δ) cos ωt + a₂ δ sin ωt

The total energy will be taken to be proportional to the time average of the square of the displacement.

Thus E = <(a₁ + a₂ cos δ)² + a₂² sin²δ> = a₁² + a₂²

As <cos δ> = 0 and we have put < cos²ωt > = < sin² ωt > = ½ and has been absorbed in the overall constant of proportionality.

In the same units, the energies of the two oscillations are a₁² and a₂² respectively so the proposition is proved.

(b) Here

and the mean square displacement is αa₁² + a₂². If δ is fixed but arbitrary. Then as in (a) we see that E = E₁ + E₂.

2. By means of plotting find the amplitude of the oscillation resulting from the addition of the following three oscillations of the same direction:

ξ₁ = a cos ωt, ξ₂ = 2a sin ωt, ξ₃ = 1.5a cos (ωt + π/3)

It is easier to do it analytically.

ξ₁ = a cos ωt, ξ₂ = 2a sin ωt,

ξ₃ = (3/2)a cosπ/3 cos ωt – sin π/3 sin ωt )

Resultant vibration is:

ξ = (7a/4)cos ωt + a(2 – 3√3/4)sin ωt

This has an amplitude = (a/4)√(49 + (8 – 3√3)²

= 1.89 a

3. A certain oscillation results from the addition of coherent oscillations of the same direction ξ_k = a cos [ωt + (k – 1) φ], where k is the number of the oscillation (k = 1, 2, . . N), φ is the phase difference between the kth and (k – 1)th oscillations. Find the amplitude of the resultant oscillation.

We use the method of complex amplitudes. Then the amplitudes are

A₁ = a, A₂ = ae^iφ, …A_N = ae^{i(N – 1)φ} and the resultant complex amplitude is

A = A₁ + A₂ + …A_N

= a(1 + e^iφ + e^2iφ+ …+e^{i(N – 1)φ})

= a(1 – e^iNiφ)/(1 – e^iφ)

The corresponding ordinary amplitude is

4. A system illustrated in Fig. 5.12 consists of two coherent point sources 1 and 2 located in a certain plane so that their dipole moments are oriented at right angles to that plane. The sources are separated by a distance d, the radiation wavelength is equal to λ. Taking into account that the oscillations of source 2 lag in phase behind the oscillations of source 1 by φ

(φ < π), find:

(a) the angles θ at which the radiation intensity is maximum;

(b) the conditions under which the radiation intensity in the direction θ = π is maximum and in the opposite direction, minimum.

With dipole moment perpendicular to the plane, there is no variation with θ of individual radiation amplitude. Then the intensity variation is due to interference only.

In the direction given by angle θ, the phase difference is

(2π/λ)d cos θ + φ = 2kπ for maxima

Thus d cos θ = (k – φ/2π)λ

k = 0, ±1, ±2, …

We have added φ to (2π/λ)d cos θ because the extra path that te wave from 2 has to travel in going to P(as compared to 1) makes it lag more than it already is due to φ.

(b) Maximum for θ = π gives -d = (k – φ/2π)λ

Minimum for θ = 0 gives d = (k’ – φ/2π + 1/2 )λ

Adding we get (k + k’ – φ/π + ½ )λ = 0

This can be true if k’ = -k, φ = π/2

Since 0< φ< π.

Then -d = (k – ¼)λ

Here k = 0, -1, -2, -3..

(otherwise R.H.S will become +ve).

5. A stationary radiating system consists of a linear chain of parallel oscillators separated by a distance d, with the oscillation, phase varying linearly along the chain. Find the time dependence of the phase difference ∆φ between the neighbouring oscillators at which the principal radiation maximum of the system will be “scanning” the surroundings with the constant angular velocity ω.

If Δφ is the phase difference between neighbouring radiators then for a maximum in the direction θ we must have

(2π/λ)d cos θ + ∆φ = 2πk

For scanning θ = ωt + β

Thus (d/λ) cos (ωt + β) + ∆φ/2π = k

Or ∆φ = 2π[k – (d/λ)cos (ωt + β)]

To get the answer of the book, put β = α – π/2.

6. In Lloyd’s maximum mirror experiment (Fig. 5.13) a light wave emitted directly by the source S (narrow slit) interferes with the wave reflected from a mirror M. As a result, an interference fringe pattern is formed on the screen Sc. The source and the mirror are separated by a distance l = 100 cm. At a certain position of the source, the fringe width on the screen was equal to ∆x= 0.25 mm, and after the source was moved away from the mirror plane by ∆h = 0.60 mm, the fringe width decreased η = 1.5 times. Find the wavelength of light.

From the general formula, ∆x = lλ/d

We find that, ∆x/η = lλ/(d + 2∆h)

Since d increases to d + 2∆h when the source is moved away from the mirror plane by ∆h.

Thus ηd = d + 2∆h

Or d = 2∆h∆x/(η-1)l

= 0.6μm.

7. Two coherent plane light waves propagating with a divergence angle ψ<<1 fall almost normally on a screen. The amplitudes of the waves are equal. Demonstrate that the distance between the neighbouring maxima on the screen is equal to ∆x = λ/ψ), where λ is the wavelength.

We can think of the two coherent plane waves as emitted from two coherent point sources very far away. Then ∆x = lλ/d = λ/d/l

But d/l = ψ (if ψ<<1)

So ∆x = λ/ψ

8. Figure 5.14 illustrates the interference experiment with Fresnel mirrors. The angle between the mirrors is α = 12′, the distances from the mirrors’ intersection line to the narrow slit S and the screen Sc are equal to r = 10.0 cm and b = 130 cm respectively. The wavelength of light is λ = 0.55 μm. Find:

(a) the width of a fringe on the screen and the number of possible maxima;

(b) the shift of the interference pattern on the screen when the slit is displaced by δl = 1.0 mm along the arc of radius r with centre at the point O;

(c) at what maximum width δ_max of the slit the interference fringes on the screen are still observed sufficiently sharp.

(a) Here S’S’’= d = 2rα

Then ∆x = (b + r)λ/2α

Putting b = 1.3 metre, r = 0.1 metre

λ = 0.55 μm, α = 12’ = 1/5×57 radian

we get ∆x = 1.1 mm

Number of possible maxima = 2bα/∆x + 1

≈ 8.3 + 1 ≈ 9

(2bα is the length of the spot on the screen which gets light after reflection from both mirror. We add 1 above to take account of the fact that in a distance ∆x there are two maxima.)

(b) when the slit moves by δl along the arc of radius r the incident ray on the mirror rotates by δl/r; this is also the rotation of the reflected ray. There is then a shift of the fringe of magnitude.

bδl/r = 13 mm.

(c) If the width of the slit is δ then we can imagine the slit to consist of two narrow slits width separation δ. The fringe pattern due to the wide slit is the superposition of the pattern due to these two narrow slits. The full pattern will not be sharp at all if the pattern due to the two narrow slits are ½ ∆x apart because then the maximum due to one will fill the minima due to the other. Thus we demand

bδ_max/r = ½ ∆x

= (b + r)λ/4rα

δ_max = (1 + r/b)λ/4α

= 42 μm.

9. A plane light wave falls on Fresnel mirrors with an angle α = 2.0′ between them. Determine the wavelength of light if the width of the fringe on the screen ∆x = 0.55 mm.

To get this case we must let r → ∞ in the formula for ∆x of the last example.

So ∆x = (b+ r)λ/2αr → λ/2α

(A plane wave is like light emitted from a point source at ∞)

Then λ = 2α∆x

= 0.64 μm.

10. A lens of diameter 5.0 cm and focal length f = 25.0 cm was cut along the diameter into two identical halves. In the process, the layer of the lens a = 1.00 mm in thickness was lost. Then the halves were put together to form a composite lens. In this focal plane a narrow slit was placed, emitting monochromatic light with wavelength λ = 0.60 μm. Behind the lens a screen was located at a distance b = 50 cm from it. Find:

(a) the width of a fringe on the screen and the number of possible maxima;

(b) the maximum width of the slit δ_max at which the fringes on the screen will be still observed sufficiently sharp.

We show the upper half of the lens. The emergent light is at an angle a/2f from the axis. Thus the divergence angle of the two incident light beams is

ψ = a/f

When they interfere the fringes produced have a width

∆x = λ/ψ = fλ/a = 0.15 mm

The patch on the screen illuminated from the by both light has a width b ψ and this contains

bψ/∆x = ba²/f²λ fringes

= 13 fringes

(If we ignore 1 in comparison to bψ/∆x (8(a)).

We follow the logic of (8 (c)). From one edge of the slit to the other edge the distance of magnitude δ (i.e. a/2 to a/2 + δ)

If we imagine the edge to shift by this distance, the angle ψ/2 will increase by ∆ψ/2 = δ/2f and the light will shift ±bδ/2f

The fringe pattern will therefore shift by δ.b/f

Equating this to ∆x/2 = fλ/2a we get

δ_max = f²λ /2ab = 37.5 μm

11. The distances from a Fresnel biprism to a narrow slit and a screen are equal to a = 25 cm and b = 100 cm respectively. The refracting angle of the glass biprism is equal to θ = 20′. Find the wavelength of light if the width of the fringe on the screen is ∆x = 0.55 mm.

∆x = lλ/d

l = a + b

d = 2(n -1)θa

δ = (n – 1)θ

d = 2δa

n = R.I of glass

Thus λ = 2(n – 1)θa∆x/(a + b)

= 0.64 μm

12. A plane light wave with wavelength λ = 0.70 μm falls normally on the base of a biprism made of glass (n = 1.520) with refracting angle θ = 5.0⁰. Behind the biprism (Fig. 5.15) there is a plane-parallel plate, with the space between them filled up with benzene (n’ = 1.500). Find the width of a fringe on the screen Sc placed behind this system.

It will be assumed that the space between the biprism and the glass plate filled with benzene constitutes complementary prisms as shown.

Then the two prisms being oppositely placed, the net deviation produced by them is

δ = (n – 1)θ – (n’ – 1)θ

= (n – n’)θ

Hence as in the previous problem

d = 2aδ

= 2aθ(n – n’)

So ∆x = (a + b)λ/2aθ(n – n’)

For plane incident wave we let a→∞

So ∆x = λ/2(n – n’)

= 0.2 mm

13. A plane monochromatic light wave falls normally on a diaphragm with two narrow slits separated by a distance d = 2.5 mm. A fringe pattern is formed on a screen placed at a distance l = 100 cm behind the diaphragm. By what distance and in which direction will these fringes be displaced when one of the slits is covered by a glass plate of thickness h = 10 μm?

Extra phase difference introduced by the glass plate is (2π/λ)(n – 1) h

This will cause a shift equal to (n – 1)h/λ fringe widths

i.e. by (n – 1)h/λ ×( lλ/d)

= (n – 1)hl/d

= 2 mm

The fringes move down if the lower slit is covered by the plate to compensate for the extra phase shift introduced by the plate.

14. Figure 5.16 illustrates an interferometer used in measurements of refractive indices of transparent substances. Here S is a narrow slit illuminated by monochromatic light with wavelength λ = 589 nm, 1 and 2 are identical tubes with air of length l = 10.0 cm each, D is a diaphragm with two slits. After the air in tube 1 was replaced with ammonia gas, the interference pattern on the screen Sc was displaced upward by N = 17 fringes. The refractive index of air is equal to n = 1.000277. Determine the refractive index of ammonia gas.

No. of fringes shifted = (n’ – n)l/λ = N

So n’ = n + Nλ/l

= 1.000377

15. An electromagnetic wave falls normally on the boundary between two isotropic dielectrics with refractive indices n₁ and n₂. Making use of the continuity condition for the tangential components, E and H across the boundary, demonstrate that at the interface the electric field vector E

(a) of the transmitted wave experiences no phase jump;

(b) of the reflected wave is subjected to the phase jump equal to π if it is reflected from a medium of higher optical density.

Suppose the vector

E_T + E’_T = E’’ (1)

where the subscript T means tangential.

Since E’’_T and E_T have the same sign , there is no phase change involved in this case,

(b) From (1) and (3)

(n₂ + n₁)E’_T + (n₂ – n₁)E_T = 0

Or E’_T = (n₁ – n₂)E_T/(n₁+ n₂)

If n₂>n₁ then E’_T and E_T have opposite signs. Thus the reflected wave has an abrupt change of phase by π if n₂> n₁ i.e. on reflection from the interface between two media when light is incident from the rarer to denser medium.

16. A parallel beam of white light falls on a thin film whose refractive index is equal to n = 1.33. The angle of indices is θ₁ = 52⁰. What must the film thickness be equal to for the reflected light to be coloured yellow (λ = 0.60 μm) most intensively?

Path difference between (1) and (2) is

2nd sec θ₂ – 2d tan θ₂ sin θ₁

= 2d(n – sin² θ₁)/n/√(1- sin² θ₁/n²)

= 2d√(n²– sin² θ₁)

For bright fringes this must equal (k + ½)λ where ½ comes from the phase change of π for (1).

Here k = 0, 1, 2, …

Thus 4d√(n² – sin²θ₁)

= (2k + 1)λ

Or d = λ(1 + 2k)/4√(n² – sin²θ₁)

= 0.41(1 + 2k) μm

17. Find the minimum thickness of a film with refractive index 1.33 at which light with wavelength 0.64 μm experiences maximum reflection while light with wavelength 0.40 μm is not reflected at all. The incidence angle of light is equal to 30⁰.

Given 2d√(n² – ¼) = (k+½)×0.64 μm (bright fringe)

2d√(n² – ¼) = k’×0.40 μm (dark fringe)

Where k, k’ are integers.

Thus 64(k + ½) = 40k’ or 4(2k + 1) = 5k’

This means, for the smallest integer solutions, k = 2, k’ = 4

Hence d = 4×0.40/2√(n² – ¼)

= 0.65 μm

18. To decrease light losses due to reflection from the glass surface the latter is coated with a thin layer of substance whose refractive index n’ = √n where n is the refractive index of the glass. In this case the amplitudes of electromagnetic oscillations reflected from both coated surfaces are equal. At what thickness of that coating is the glass reflectivity in the direction of the normal equal to zero for light with wavelength λ?

When the glass surface is coated with a material of R.I. n’ = √n(n = R.I of glass) of appropriate thickness, reflection is zero because of interference between various multiply reflected waves. We show this below.

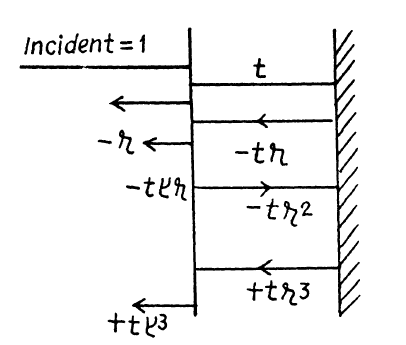
Let a wave of unit amplitude be normally incident from the left. The reflected amplitude is -r where r = (√n – 1)/(√n + 1)

Its phase is -ve so we write the reflected wave as -r. The transmitted wave has amplitude t

t = 2/(1 + √n)

This wave is reflected at the second face and has amplitude -tr

(because (n – √n)/(n+√n) = (√n – 1)/(√n + 1)

The emergent wave has amplitude -tt’r.

We prove below that -t t’ = 1 – r².

There is also a reflected part of amplitude t r r’ = -tr² where r’ is the reflection coefficient for a ray incident from the coating towards air. After reflection from the second face a wave of amplitude

t t’ r³ = +(1 – r²)r³

emerges . Let δ be the phase of the wave after traversing the coating both ways. Then the complete reflected wave is

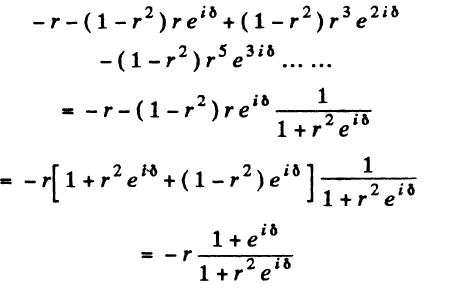
This vanishes if δ = (2k + 1)π.

But δ = (2π/λ)2√n d

So d = (λ/4√n)(2k + 1)

We now deduce t t’ = 1 – r² and r’ = + r. This follows from the principle of reversibility of light path as shown in the figure below.

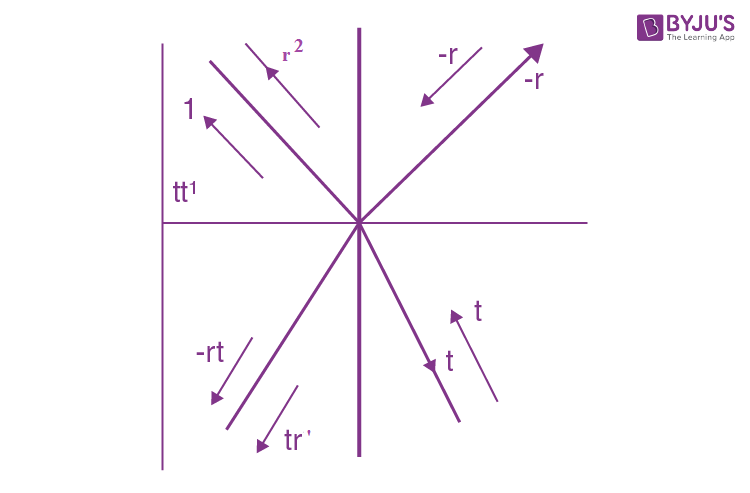
t t’ + r² = 1

-rt + r’t = 0

So t t’ = 1 – r²

r’ = + r

(-r is the reflection ratio for the wave entering a denser medium).

19. Diffused monochromatic light with wavelength λ = 0.60 μm falls on a thin film with refractive index n = 1.5. Determine the film thickness if the angular separation of neighbouring maxima observed in reflected light at the angles close to θ = 45⁰ to the normal is equal to δθ = 3.0⁰.

We have the condition for maxima

2d√(n² – sin² θ₁) = (k + ½) λ

This must hold for angle (θ + δθ/2) with successive values of k. Thus

2d√(n² – sin² (θ + δθ/2)) = (k – ½) λ

Thus λ = 2d[√(n² – sin²θ + δθ sin θ cos θ) – √(n² – sin²θ – δθ sin θ cos θ)]

= 2d( δθ sin θ cos θ)/√(n² – sin²θ)

Thus d = √(n² – sin²θ λ)/sin 2θ δθ

= 15.2μm

20. Monochromatic light passes through an orifice in a screen Sc (Fig. 5.17) and being reflected from a thin transparent plate P produces fringes of equal inclination on the screen. The thickness of the plate is equal to d, the distance between the plate and the screen is l, the radii of the ith and kth dark rings are r_i and r_k. Find the wavelength of light taking into account that r_i.k << l.

For small angles θ we write for dark fringes

2d√(n² – sin² θ) = 2d(n – sin²θ/2n)

= (k + 0)λ

For the first dark fringe, θ ≅ 0 and

2dn = (k₀ + 0)λ

For the i^th dark fringe

2d(n – sin² θ_i/2n) = (k₀ – i + 1)λ

Or sin²θ_i = (nλ/d)(i – 1)

= r_i²/4l²

Finally (nλ/d)(i – k) = (r_i² – r_k²)/4l²

λ = d(r_i² – r_k²)/4l²n(i – k)