Important Electrostatics Formulas For JEE

Electrostatics deals with the charges at rest. Charge of a material body or particle is the property due to which it produces and experiences electrical and magnetic effects. Some of the naturally occurring charged particles are electrons, protons etc. Unit of charge is Coulomb.

Download Complete Chapter Notes of Electrostatic Potential and Capacitance
Download Now

Electrostatics Formulas for JEE

1. Coulombs force between two-point charges

Coulomb's law

\(\begin{array}{l}\vec{F}=\frac{1}{4\pi\epsilon _{0}}\frac{q_{1}q_{2}}{\left | \vec{r}\right |^{2}}\hat{r}\end{array} \)

Here k= 1/4πε₀= 9 x 10⁹ Nm²/C²

q₁ and q₂ are the charges separated by a distance r

2. Electric field

The electric field at a distance r from the charge q

\(\begin{array}{l}\vec{E}=\frac{1}{4\pi\epsilon _{0}}\frac{q}{{\left |\vec{r} \right |^{2}}}\hat{r}\end{array} \)

3. Electric field Intensity

\(\begin{array}{l}\vec{E}=\vec{F}/q\end{array} \)

Where F is the force on the charge q due to the electric field E

4. Electrostatic Energy

\(\begin{array}{l}{U}=\frac{1}{4\pi\epsilon _{0}}\frac{q_{1}q_{2}}{r}\end{array} \)

q₁,q₂ are the charges

r is the distance between the charges

5. Electric Potential

\(\begin{array}{l}V=\frac{1}{4\pi\epsilon _{0}}\frac{q}{r}\end{array} \)

\(\begin{array}{l}dV=-\vec{E}.\vec{r}\end{array} \)

\(\begin{array}{l}V(\vec{r})=-\int_{\infty }^{\vec{r}}\vec{E}.d{\vec{r}}\end{array} \)

6. Electric dipole moment

It is the product of a charge (q) and the distance between the two charges (d)

Electric dipole moment

\(\begin{array}{l}\vec{p}=q\vec{d}\end{array} \)

7. Potential of a dipole

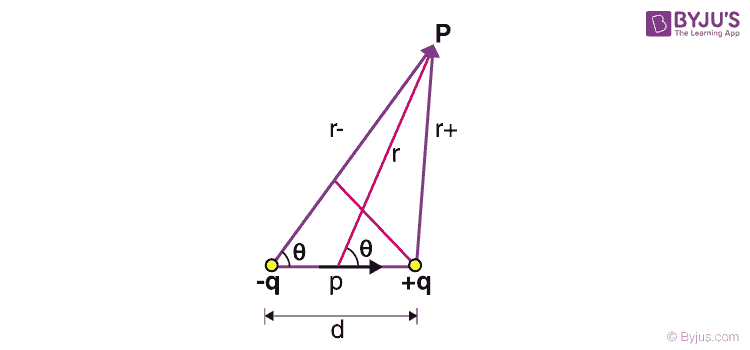
Potential of a dipole

\(\begin{array}{l}V=\frac{1}{4\pi \epsilon _{0}}\frac{pcos\theta }{r^{2}}\end{array} \)

8. Field of a dipole

Field due to dipole

\(\begin{array}{l}E_{+}=\frac{1}{4\pi \epsilon _{0}}\frac{2pcos\theta }{r^{3}}\end{array} \)

\(\begin{array}{l}E=\frac{1}{4\pi \epsilon _{0}}\frac{pcos\theta }{r^{3}}\end{array} \)

9. Torque on a dipole placed in the electric field

\(\begin{array}{l}\vec{\tau }=\vec{p}\times \vec{E}\end{array} \)

10. Potential energy of a dipole

\(\begin{array}{l}U=-\vec{p}.\vec{E}\end{array} \)

Important Electrostatics Formulas For JEE

Electrostatics Formulas for JEE

Electrostatics – Electric Field Lines and Electric Flux

Electrostatics – Electric Field and Electric Dipole

Top 10 Important Questions of Electrostatic Potential and Capacitance

Comments

Leave a Comment Cancel reply

FREE TEXTBOOK SOLUTIONS