Important Simple Harmonic Motion Formulas For JEE Main and Advanced

If the restoring force/torque acting on the body in oscillatory motion is directly proportional to the displacement of the body and is always directed towards the equilibrium position, then the motion is called Simple Harmonic Motion (SHM). Find all the equations and formulas related to Simple Harmonic Motion on this page.

Simple Harmonic Motion Formulas

1. General Equation of SHM

Displacement x =A sin(ωt + Φ)

Here (ωt + Φ) is the phase of the motion, and Φ is the initial phase of the motion

2. Angular Frequency (ω)

ω = 2π/T = 2πf

T is the time period

f is the frequency

3. Frequency (f):

Number of oscillations completed in the unit time interval

f = 1/T = ω/2π

4. Time Period (T)

T = 2π/ω

5. Hooke’s law

Force (F) = -kx (for small elongation x)

k is the spring constant

6. Acceleration

a = -ω²x = -ω² A sin(ωt + Φ)

7. Velocity

v = Acos(ωt+ Φ)

Φ is the initial phase of motion

8. Potential Energy

U = ½ kx² (as a function of x)

9. Kinetic Energy

K = ½ mω²(A² – x²)

K = ½ k(A² – x²)

10. Total Energy

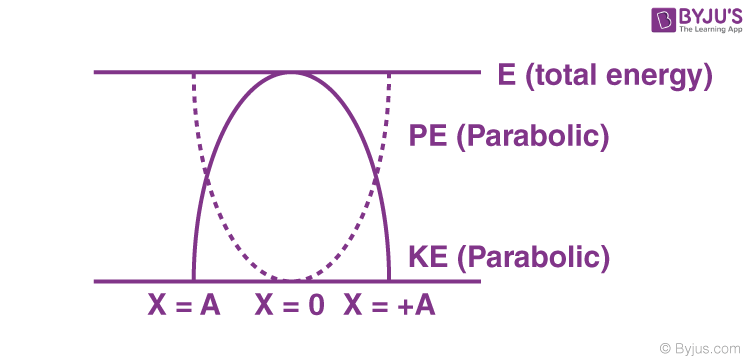
E = U+K

E= ½ mω²A²

11. Simple Pendulum

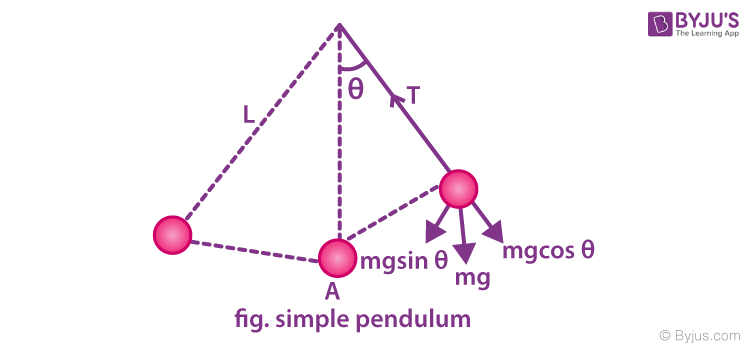
l is the length of the pendulum

12. Physical Pendulum

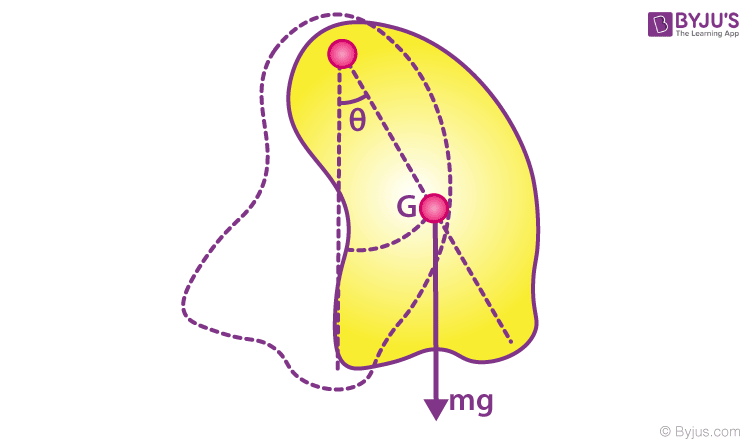
Here I= I_cm + ml ²

l is the distance between the point of suspension and the centre of mass.

13. Torsional Pendulum

k is the torsional constant

14. Springs in parallel

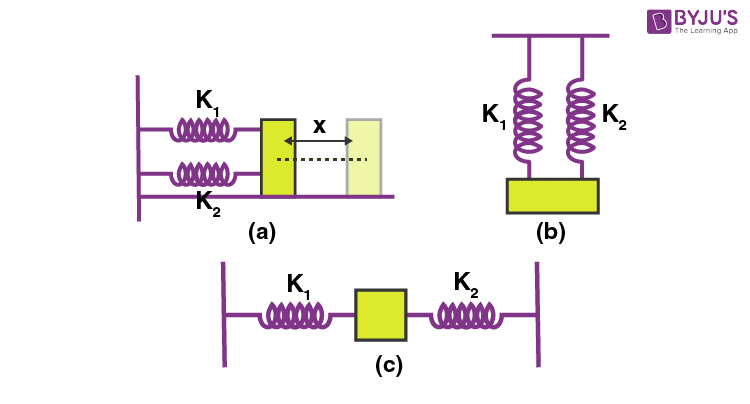
K_eq = k₁+k₂

15. Springs in series

1/k_eq = 1/k₁ + 1/k₂

UP Next: Important Centre of Mass Formulas for JEE