JEE is an examination conducted for admission into various institutions across the country. The questions asked in the examination are based on Class 11 and Class 12 syllabus. The JEE aspirants can refer to this page to find the answers for all the questions asked in JEE 2019 April Physics paper. These answers are provided by the subject experts at BYJU’S.
JEE Advanced 2019 Question Paper
April Paper – Physics
April Paper – Physics
1. A capacitor of capacitance C = 15 pF is charged with voltage V = 500 V. The electric field inside the capacitor with dielectric is 106 V/m and the area of the plate is 10– 4 m2, then the dielectric constant of the medium is: (
a.12.47
b.8.47
c.10.85
d.14.85
\(\begin{array}{l}{{\varepsilon }_{0}}=8.85\times {{10}^{-12}}\end{array} \)
in SI units) a.12.47
b.8.47
c.10.85
d.14.85
C = 15PF
V = 500V
E = 106 V/m
A = 10– 4 m2
\(\begin{array}{l}C=\frac{k{{\varepsilon }_{0}}A}{d}\end{array} \)
\(\begin{array}{l}d=\frac{k{{\varepsilon }_{0}}A}{C}\end{array} \)
E = V/d
\(\begin{array}{l}E= \frac{500 C}{k{{\varepsilon }_{0}}A}\end{array} \)
\(\begin{array}{l}K=\frac{Vc}{A{{\varepsilon }_{0}}E}=\frac{500\times 15\times {{10}^{-12}}}{{{10}^{-4}}\times {{10}^{6}}\times 8.85\times {{10}^{-12}}}\end{array} \)
= 8.47
Answer: (b)
2. The electric field of EM wave is 6 volt/m. The magnetic field associated with the wave if the wave is propagating in the +x direction and electric field along y-axis is:
a.
b.
c.
d.
a.
\(\begin{array}{l}{{10}^{-8}}T\hat{K}\end{array} \)
b.
\(\begin{array}{l}2\times {{10}^{-8}}T\hat{K}\end{array} \)
c.
\(\begin{array}{l}3\times {{10}^{-8}}T\hat{K}\end{array} \)
d.
\(\begin{array}{l}4\times {{10}^{-8}}T\hat{K}\end{array} \)
E = BC
\(\begin{array}{l}B =\frac{E}{C}=\frac{6}{3\times {{10}^{8}}}=2\times {{10}^{-8}}T(along\,z-axis)\end{array} \)
Answer: (b)
3. An electron of H-atom de-exits from energy level m1 = 2 to h2 = 1 and the emitted photon is incident on He+ ion in ground state and first ox cited states which of following transition is possible.
a. n = 1 to n = 4
b. n = 2 to n = 4
c. n = 2 to n = 3
d. n = 1 to n = 4
a. n = 1 to n = 4
b. n = 2 to n = 4
c. n = 2 to n = 3
d. n = 1 to n = 4
\(\begin{array}{l}{{E}_{H}}=13.6\left\{ \frac{1}{{{1}^{2}}}-\frac{1}{{{2}^{2}}} \right\}=10.2\,ev\end{array} \)
\(\begin{array}{l}{{E}_{H}}=13.6{{(2)}^{2}}\left\{ \frac{1}{{{2}^{2}}}-\frac{1}{{{n}^{2}}} \right\}\end{array} \)
substituting options n = 4
Answer: (b)
4. The switch is closed at t = 0. The time after which the rate of dissipation of energy in the resistor is equal to rate at which energy is being store in the inductor is:
a.
\(\begin{array}{l}\ell n2\end{array} \)
b.
\(\begin{array}{l}{}^{1}/{}_{2}\ell n2\end{array} \)
c.
\(\begin{array}{l}{}^{1}/{}_{4}\ell n2\end{array} \)
d.
\(\begin{array}{l}2\ell n2\end{array} \)
\(\begin{array}{l}i=\frac{E}{R}(1-e^{-\frac{Rt}{L}})\end{array} \)
\(\begin{array}{l}\frac{di}{dt}=\frac{E}{L}e^{-\frac{t}{\tau }}\end{array} \)
,where \(\begin{array}{l}\tau =\frac{L}{R}\end{array} \)
\(\begin{array}{l}i^{2}R=(L\frac{di}{dt})\end{array} \)
\(\begin{array}{l}\frac{E}{R}R(1-e^{-\frac{t}{\tau }})=L \frac{E}{L}e^-{\frac{t}{\tau }}\end{array} \)
1 = 2e-e/ Ï„
ln2 = t/ Ï„
t = Ï„ ln2
Answer: (a)
5. Two identical containers of same emissivity containing liquids A & B at same temperature of 60°c initially and densities PA and PB respectively. Where, PA< PB. Which plot best represents the temperature variation of both with time? Given
\(\begin{array}{l}\left( \begin{matrix} {{S}_{A}}=100\frac{J}{kg-{{k}^{1}}} \\ {{S}_{B}}=2000\frac{J}{kg-k} \\ \end{matrix} \right)\end{array} \)
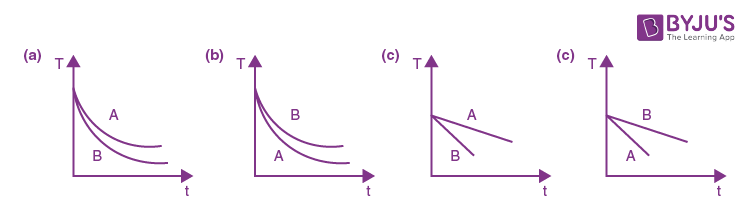
.\(\begin{array}{l}\frac{d\theta }{dt}=\frac{\theta eA\left( T_{0}^{m}-T_{0}^{A} \right)}{ms}\end{array} \)
\(\begin{array}{l}\frac{d\theta }{dt}\alpha \frac{1}{ms}\end{array} \)
Answer: (b)
6. The system of 2 rods shown in fig is vibrating at the same frequency and forming a standing wave. The ratio of the number of antinodes in the two rods if radius of rod B is twice the radius of A is:
a.1
b.2
c.3
d.4
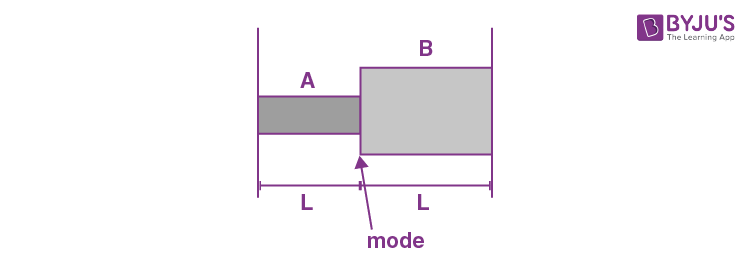
a.1
b.2
c.3
d.4
\(\begin{array}{l}f_{1} = \frac{n}{2l}\sqrt{\frac{T}{\rho A}}f_{2} = \frac{m}{2l}\sqrt{\frac{T}{\rho 4A}}\end{array} \)
Given f1 = f2
\(\begin{array}{l}\frac{f_{1}}{f_{2}} = \frac{n}{m}\times 2\end{array} \)
\(\begin{array}{l}\frac{n}{m}\times 2\end{array} \)
Answer: (b)
7. At the given instant the four particles having masses and acceleration as shown in the fig lie at vertices of a square. Acceleration of the mass of the system is:
a.
b.
c.
d.
a.
\(\begin{array}{l}\frac{1}{5}\left( \hat{i}+\hat{j} \right)\end{array} \)
b.
\(\begin{array}{l}\frac{1}{5}\left( \hat{j}-\hat{i} \right)\end{array} \)
c.
\(\begin{array}{l}\frac{1}{5}\left( \hat{i}-\hat{j} \right)\end{array} \)
d.
\(\begin{array}{l}\frac{1}{5}\left( \hat{i}+\hat{j} \right)\end{array} \)
\(\begin{array}{l}{{a}_{am}}=\frac{{{m}_{1}}{{a}_{1}}+{{m}_{2}}{{a}_{2}}+{{m}_{3}}{{a}_{3}}+{{m}_{4}}{{a}_{4}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+{{m}_{4}}}\end{array} \)
\(\begin{array}{l}=\frac{m\left( -a\hat{i} \right)+2m\left( a\hat{j} \right)+3m\left( a\hat{i} \right)+4m\left( -a\hat{j} \right)}{m+2m+3m+4m}\end{array} \)
=
\(\begin{array}{l}\frac{2i-2\hat{j}}{10}=\left( \frac{{\hat{i}}}{5}-\frac{{\hat{j}}}{5} \right)\end{array} \)
Answer: c
8. In YDSE ratio of Amplitude of wave is 1: 3. The ratio of I max: I min is:
a. 1: 4
b. 4: 1
c. 1: 1
d. 1: 9
a. 1: 4
b. 4: 1
c. 1: 1
d. 1: 9
\(\begin{array}{l}\frac{{{I}_{max}}}{{{I}_{min}}}={{\left( \frac{{{A}_{1}}+3{{A}_{1}}}{{{A}_{1}}-3{{A}_{1}}} \right)}^{2}}=\frac{4}{1}\end{array} \)
Answer: (b)
9. Two particles are moving perpendicular to each other with de-Broglie wave length λ1 and λ2 if they collide and stick then the de-Broglie wave length of system after collision is:
a.
b.
c.
d.
a.
\(\begin{array}{l}\lambda =\frac{{{\lambda }_{1}}{{\lambda }_{2}}}{\sqrt{\lambda _{1}^{2}+\lambda _{2}^{2}}}\end{array} \)
b.
\(\begin{array}{l}\lambda =\frac{{{\lambda }_{1}}}{\sqrt{\lambda _{1}^{2}+\lambda _{2}^{2}}}\end{array} \)
c.
\(\begin{array}{l}\frac{\sqrt{\lambda _{1}^{2}+\lambda _{2}^{2}}}{{{\lambda }_{2}}}\end{array} \)
d.
\(\begin{array}{l}\lambda =\frac{{{\lambda }_{1}}{{\lambda }_{2}}}{\sqrt{{{\lambda }_{1}}+{{\lambda }_{2}}}}\end{array} \)
Pi + Pj = P
\(\begin{array}{l}\frac{h}{{{\lambda }_{1}}}\hat{1}+\frac{h}{{{\lambda }_{2}}}\hat{j}=\frac{h}{\lambda }\end{array} \)
\(\begin{array}{l}\frac{1}{\lambda }=\sqrt{\frac{1}{{{\lambda }_{1}}}+\frac{1}{{{\lambda }_{2}}}}\end{array} \)
\(\begin{array}{l}\lambda =\frac{{{\lambda }_{1}}{{\lambda }_{2}}}{\sqrt{\lambda _{1}^{2}+\lambda _{2}^{2}}}\end{array} \)
Answer: (a)
10. Ship moving with velocity
a. 2.6
b. 2.2
c. 2.4
d. None
\(\begin{array}{l}{{\vec{V}}_{1}}=30\hat{i}+50\hat{j}\end{array} \)
from position (0, 0) and ship B moving with velocity \(\begin{array}{l}\overrightarrow{{{V}_{2}}}=-10\hat{i}\end{array} \)
from position (80, 150). The time for minimum separation is a. 2.6
b. 2.2
c. 2.4
d. None
\(\begin{array}{l}{{V}_{1}}=30\hat{i}+50\hat{j}\end{array} \)
\(\begin{array}{l}r=-80\hat{i}-150\hat{j}\end{array} \)
\(\begin{array}{l}{{V}_{2}}=-10\hat{i}\end{array} \)
\(\begin{array}{l}\vec{v} = 40i + 50j\end{array} \)
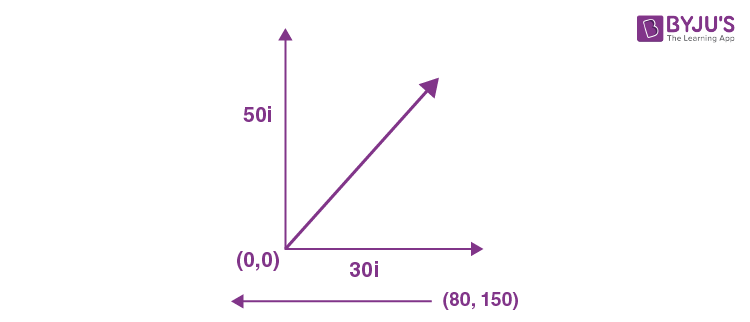
Component of V1 along r is
\(\begin{array}{l}\frac{V.r}{{{V}^{2}}}=2.6\end{array} \)
Answer: (a)
11. A carbon resistance with color bard is 200 Ω. If red bard is replaced by green bard then the new resistance is
a. 500 Ω
b. 300 Ω
c. 400 Ω
d. 100 Ω
a. 500 Ω
b. 300 Ω
c. 400 Ω
d. 100 Ω
Red 2
Green 5
New resistance 500 Ω
Answer: (a)
12. Dimension of
a.
b.
c.
d.
\(\begin{array}{l}\sqrt{\frac{{{\varepsilon }_{0}}}{{{\mu }_{0}}}}\end{array} \)
area.
\(\begin{array}{l}\left[ M{{L}^{2}}{{T}^{-3}}{{A}^{-2}} \right]\end{array} \)
b.
\(\begin{array}{l}\left[ {{M}^{-1}}{{L}^{-2}}{{T}^{3}}{{A}^{2}} \right]\end{array} \)
c.
\(\begin{array}{l}\left[ {{M}^{2}}{{L}^{2}}{{T}^{-3}}{{A}^{-2}} \right]\end{array} \)
d.
\(\begin{array}{l}\left[ {{M}^{-1}}{{L}^{2}}{{T}^{3}}{{A}^{2}} \right]\end{array} \)
\(\begin{array}{l}\sqrt{\frac{\varepsilon {}_{0}}{{{\mu }_{0}}}}=\sqrt{\frac{{{\varepsilon }_{0}}{{\varepsilon }_{0}}}{{{\mu }_{0}}{{\varepsilon }_{0}}}}\Rightarrow {{\varepsilon }_{0}}.C\end{array} \)
\(\begin{array}{l}\frac{Co{{l}^{2}}}{N{{m}^{2}}}(m/s)=\frac{{{I}^{2}}{{T}^{2}}\not{L}{{T}^{-1}}}{M\not{L}{{T}^{-2}}{{L}^{2}}}\end{array} \)
\(\begin{array}{l}=\left[ {{M}^{-1}}{{L}^{-2}}{{T}^{3}}{{A}^{2}} \right]\end{array} \)
Answer: (b)
13. A electric circuit is shown in figure. The potential different between the points A & B is:
a.
b.
c.
d.
a.
\(\begin{array}{l}\frac{10}{3}\end{array} \)
b.
\(\begin{array}{l}\frac{20}{3}\end{array} \)
c.
\(\begin{array}{l}\frac{5}{3}\end{array} \)
d.
\(\begin{array}{l}\frac{7}{3}\end{array} \)
Using nodal method
\(\begin{array}{l}\frac{{{V}_{A}}-2}{2\Omega }+\frac{{{V}_{A}}-4}{2}+\frac{{{V}_{A}}-4}{2}=0\end{array} \)
\(\begin{array}{l}\frac{V^{A}}{2}-1+\frac{V^{A}}{2}-2+\frac{V^{A}}{2}-2=0\end{array} \)
\(\begin{array}{l}V^{A}\left( {}^{1}/{}_{2}+{}^{1}/{}_{2}+{}^{1}/{}_{2} \right)=5\end{array} \)
\(\begin{array}{l}{{V}_{A}}=\left( \frac{3}{2} \right)=5\end{array} \)
\(\begin{array}{l}{{V}_{A}}\frac{10}{3}\end{array} \)
Answer: (a)
14. 10 particles each of mass 10-26 kg are striking perpendicularly on a wall of area 1 m2 with speed 104 m/s in 1 sec. The pressure on the wall if collision are perfectly elastic is:
a. 2 N/m2
b. 4 N/m2
c. 6 N/m2
d. 8 N/m2
a. 2 N/m2
b. 4 N/m2
c. 6 N/m2
d. 8 N/m2
Collision Frequency = 1022
ΔP per particle = mV2
\(\begin{array}{l}F=\frac{\Delta P}{1\sec }={{10}^{22}}\times mv\end{array} \)
=
\(\begin{array}{l}{{10}^{22}}\times {{10}^{-26}}\times 2\times {{10}^{4}}=2\end{array} \)
\(\begin{array}{l}P={}^{F}/{}_{A}={}^{2}/{}_{1}=2\end{array} \)
N/m2
Answer: (a)
15. An elastic string of Length 42 cm and cross section area 10–4 m2 is attached between two pegs at distance 6mm as shown in the figure. A particle of mass m is kept at mid point of string stretched as shown in figure by 20 cm and released. As the string attains natural Length, the particle attains a speed of 20 m/s. Then young modulus Y of string is of order.
a. 108
b. 1012
c. 106
d. 104
a. 108
b. 1012
c. 106
d. 104
Elastic stream energy × volume = kinetic energy
\(\begin{array}{l}Vol\times \frac{1}{2}stress\,\times strain={}^{1}/{}_{2}m{{v}^{2}}\end{array} \)
\(\begin{array}{l}Vol\times \frac{1}{2}\frac{stress}{strain}.strai{{n}^{2}}={}^{1}/{}_{2}m{{v}^{2}}\end{array} \)
\(\begin{array}{l}=\,{}^{1}/{}_{2}y{{(strain)}^{2}}vol={}^{1}/{}_{2}m{{v}^{2}}\end{array} \)
\(\begin{array}{l}Y=\frac{m\times {{v}^{2}}}{AL{{\left( \frac{\Delta \ell }{\ell } \right)}^{2}}}\end{array} \)
Y = [(0.05 x400 x0.42)/(0.2)2 x 10-4]
Y = 2.1 x 106 N/m2
Answer: (c)
16. The density of a circular disc is given as σ =
a.
b.
c.
d.
\(\begin{array}{l}{{p}_{0}}X\end{array} \)
where ‘X’ is the distance from the centre. Its moment of interia about an axis perpendicular to interia about an axis perpendicular to its plane and passing through its edge is: a.
\(\begin{array}{l}\frac{15}{16}{{P}_{0}}\pi {{R}^{5}}\end{array} \)
b.
\(\begin{array}{l}\frac{16}{15}{{P}_{0}}\pi {{R}^{5}}\end{array} \)
c.
\(\begin{array}{l}\frac{6}{5}{{P}_{0}}\pi {{R}^{5}}\end{array} \)
d.
\(\begin{array}{l}\frac{5}{6}{{P}_{0}}\pi {{R}^{5}}\end{array} \)
Using parallel axis
dI = dmx2 + d MR2
\(\begin{array}{l}dI=\int{{{P}_{0}}2\pi {{x}^{2}}dx.{{x}^{2}}+}\int{{{P}_{0}}}2\pi {{x}^{2}}dx{{R}^{2}}\end{array} \)
\(\begin{array}{l}=\frac{{{P}_{0}}2\pi R^{5}}{5}+\frac{{{P}_{0}}2\pi {{R}^{5}}}{3}=\frac{16{{P}_{0}}\pi {{R}^{5}}}{15}\end{array} \)
Answer: (b)
17. The circuit shown in the figure. Determine the current through Zener diode. (Given: Zener diode break down. Voltage V2 = 5.6 V)
a. 7 mA
b. 17 mA
c. 10 mA
d. 15 mA
a. 7 mA
b. 17 mA
c. 10 mA
d. 15 mA
I1 = I2 + Iz
\(\begin{array}{l}\frac{3.4}{200}={{I}_{2}}+\frac{5.6}{800}\end{array} \)
I2 = 10 mA.
Answer: (c)
18. A small sphere of mass m = 2gm having charge Q = 5 mc is suspended using an insulated string as shown in figure. The angle ÆŸ made by the sphere with vertical if it is placed in an electric field of magnitude 2000 y/m towards right is
a. tan–1 (5)
b. tan–1 (0.5)
c. tan–1 (2)
d. tan–1 (0.2)
a. tan–1 (5)
b. tan–1 (0.5)
c. tan–1 (2)
d. tan–1 (0.2)
F = mg tan ÆŸ
\(\begin{array}{l}\tan \theta =\frac{F}{mg}\end{array} \)
\(\begin{array}{l}
\(\begin{array}{l}\theta = \tan ^{-1}\left( \frac{QE}{mg} \right)\end{array} \)
\(\begin{array}{l}={{\tan }^{-1}}\left( \frac{5\times {{10}^{-6}}\times 2000}{7\times {{10}^{-3}}\times 10} \right)\end{array} \)
\(\begin{array}{l}={{\tan }^{-1}}\left( \frac{1}{2} \right)={{\tan }^{-1}}(0.5)\end{array} \)
Answer: (b)
19. A circular loop of radius r having N number of turns carries current I is placed in a uniform magnetic field
a.
b.
c.
d.
\(\begin{array}{l}\overrightarrow{B}\end{array} \)
parallel to the plane of the loop. The torque on the loop is a.
\(\begin{array}{l}N\ell \pi {{r}^{2}}B\end{array} \)
b.
\(\begin{array}{l}{{N}^{2}}\ell \pi {{r}^{2}}B\end{array} \)
c.
\(\begin{array}{l}N{{\ell }^{2}}\pi {{r}^{2}}B\end{array} \)
d.
\(\begin{array}{l}N\ell \pi {{r}^{2}}{{B}^{2}}\end{array} \)
τ = M × B
= MB sin ÆŸ
= NI πr2 ×B(1)
= NI πr2B
Answer: (a)
20. A conducting sphere is enclosed by a hollow conducting shell. Initially the inner sphere has a charge Q. While the outer one is un charged. The potential difference between the two spherical surface is found to be V. Later on the outer shell is given a charge – 4Q. The new potential difference between the two surface.
a. 1V
b. – IV
c. – 2V
d. 2V
a. 1V
b. – IV
c. – 2V
d. 2V
\(\begin{array}{l}{{V}_{A}}=\frac{KQ}{a}+\frac{K(-Q+Q)}{b}\end{array} \)
\(\begin{array}{l}{{V}_{B}}=\frac{KQ}{b}+\frac{K(-Q+Q)}{b}\end{array} \)
\(\begin{array}{l}\Delta V=KQ\left( {}^{1}/{}_{a}-{}^{1}/{}_{b} \right)\end{array} \)
\(\begin{array}{l}{{V}_{A}}=\frac{KQ}{a}-\frac{K4Q}{b}\end{array} \)
\(\begin{array}{l}{{V}_{B}}=\frac{KQ}{b}-\frac{K4Q}{b}\end{array} \)
ΔV = V
21. Four particle each of mass m are undergoing circular motion under the influence of action of their mutual gravitational interaction while being at the vertices of a square of side a. Their speeds are
a.
b.
c.
d.
a.
\(\begin{array}{l}\sqrt{\frac{2GM}{a}}\end{array} \)
b.
\(\begin{array}{l}1.16\sqrt{\frac{GM}{a}}\end{array} \)
c.
\(\begin{array}{l}1.5\sqrt{\frac{2M}{a}}\end{array} \)
d.
\(\begin{array}{l}\sqrt{\frac{GM}{a}}\end{array} \)
Gravitation Force = mv2/r
r =
\(\begin{array}{l}\sqrt{a^{2}-(\frac{a}{\sqrt{2}})^{2}}=\frac{a}{\sqrt{2}}\end{array} \)
\(\begin{array}{l}\frac{G{{m}^{2}}}{a^{2}}cos45^{0}+\frac{G{{m}^{2}}}{(\sqrt{2}a)^{2}}+\frac{G{{m}^{2}}}{a^{2}}cos45^{0}=mv^{2}/(a/\sqrt{2})\end{array} \)
\(\begin{array}{l}\frac{G{{m}^{2}}}{a^{2}}[\frac{1}{\sqrt{2}}+\frac{1}{2}+\frac{1}{\sqrt{2}}]=(mv^{2}\sqrt{2})/a\end{array} \)
\(\begin{array}{l}v^{2}=1.35(\frac{GM}{a})\end{array} \)
\(\begin{array}{l}1.16\sqrt{\frac{GM}{a}}\end{array} \)
Answer: (b)
22. A converging lens of focal length 20 cm is placed between an object & a concave mirror of focal mirror of focal length 10 cm as shown in figure. The final image is
a. Coinciding with object, enlarged, Inverted real
b. Coinciding with object, same size, erect, real
c. Coinciding with object, same size, Inverted, Vertical
d. Coinciding with object, same size, Inverted, real
a. Coinciding with object, enlarged, Inverted real
b. Coinciding with object, same size, erect, real
c. Coinciding with object, same size, Inverted, Vertical
d. Coinciding with object, same size, Inverted, real
Coinciding with object, same size, Inverted, real
Answer: (d)
23. A conducting slider of resistance R (10 Ω) mass 50 g & length 10 cm is kept on a U – shaped frame as shown in figure. There is uniform magnetic field (B = 0.1T) perpendicular to plane of frame. These slider is attached to a spring (K = 0.5 N/m). It is displaced by AƟ& released time is which amplitude become A /e is
a. 9000 s
b. 10000 s
c. 12000 s
d. 15000 s
a. 9000 s
b. 10000 s
c. 12000 s
d. 15000 s
\(\begin{array}{l}-Kx-i\ell B=m\frac{{{d}^{2}}x}{d{{\ell }^{2}}}\end{array} \)
\(\begin{array}{l}-Kx-\frac{{{B}^{2}}{{\ell }^{2}}}{R}\frac{dx}{d\ell }-m\frac{{{d}^{2}}x}{d{{\ell }^{2}}}=0\end{array} \)
Comparing with
\(\begin{array}{l}-Kx-b\frac{dx}{dt}-m\frac{{{d}^{2}}x}{d{{\ell }^{2}}}=0\end{array} \)
&
A = A0e(-b/2m)t
\(\begin{array}{l}\frac{{{B}^{2}}{{\ell }^{2}}}{R.2m}t=1\end{array} \)
\(\begin{array}{l}t=\frac{2mR}{{{B}^{2}}{{\ell }^{2}}}=10,000s\end{array} \)
Answer: b
24. An A.C source of voltage V = 220 sin (100 πt) volts is connected with R = 50 Ω. The time interval in which the current goes from its peak value to half of the peak value is
a.
b.
c.
d.
a.
\(\begin{array}{l}\frac{1}{400}\sec\end{array} \)
b.
\(\begin{array}{l}\frac{1}{50}\sec\end{array} \)
c.
\(\begin{array}{l}\frac{1}{300}\sec\end{array} \)
d.
\(\begin{array}{l}\frac{1}{200}\sec\end{array} \)
For oscillation to go from max to half is T / 6
\(\begin{array}{l}=\frac{1}{50\times 6}=\frac{1}{300}\sec\end{array} \)
Answer: (c)
25. Force displacement graph of a particle starting from rest is given in the figure shown. The kinetic energy of particle at x = 3m is
a. 6.5 J
b. 7.5 J
c. 6 J
d. 5 J
a. 6.5 J
b. 7.5 J
c. 6 J
d. 5 J
Area under graph is work done
\(\begin{array}{l}w=2\times 2+\frac{1}{2}\times (2+3)\times 1\end{array} \)
= 6.5J
Answer: (a)
26. Find out the no of reflection after which light ray will exit from (Given sin 40° = 0.64)
a. 130000
b. 57803
c. 140000
d. 150000
a. 130000
b. 57803
c. 140000
d. 150000
\(\begin{array}{l}x=\frac{20mm}{\tan r}=20\sqrt{3}m\end{array} \)
For one reflection
\(\begin{array}{l}nx=20\sqrt{3}m=2m\end{array} \)
∴
\(\begin{array}{l}n=\frac{2}{20\sqrt{3}\times {{10}^{-6}}m}\end{array} \)
= 57803
Answer: (b)
27. A block of mass 4 kg is suspended from the ceiling with the help of a steel wire off radius 2 mm and negligible mass. Find the stress in the wire (g = π2)
a. 4 × 106
b. 3 × 105
c. 3.14 × 106
d. 2 × 106
a. 4 × 106
b. 3 × 105
c. 3.14 × 106
d. 2 × 106
\(\begin{array}{l}stress=\frac{F}{A}=\frac{mg}{\pi {{r}^{2}}}\end{array} \)
\(\begin{array}{l}\frac{m{{\pi }^{\not{2}}}}{\not{\Pi}{{r}^{^{2}}}}=\frac{4\pi }{{{r}^{2}}}\end{array} \)
= 3.14 × 106 N/m2
Answer: (c)
28. A liquid of coefficient of viscosity
a. 3536
b. 3500
c. 3400
d. 3600
\(\begin{array}{l}\eta =1\end{array} \)
poise is flowing in a pipe of radius 3 cm on such that the rate of volume flow is 1000 / min. determine the Reynolds numbers.a. 3536
b. 3500
c. 3400
d. 3600
\(\begin{array}{l}\eta\end{array} \)
= 1 poise
r = 3 cm
\(\begin{array}{l}\frac{dv}{dt}=1000\,{}^{\ell }/{}_{\min }\end{array} \)
\(\begin{array}{l}Reynolds Number {R}_{e}=\frac{\rho vD}{\eta }\end{array} \)
\(\begin{array}{l}=\frac{1000}{0.1}\times \frac{1}{60\pi {{r}^{2}}}2r\end{array} \)
= 3536
Answer: (a)
Video Lessons – Physics Paper April
JEE Main 2019 April Physics Paper with Solutions
Comments