a. 8 and 6
b. 4 and 6
c. 8 and 8
d. 4 and 8
Here, we have to count S − O single bonds as well as S = O in S2O82–, as each double bond also has one sigma bond. The structure of S2O82- and S8 is shown below:

a. London dispersion, dipole-dipole and hydrogen bonding
b. hydrogen bonding and London dispersion
c. dipole-dipole and hydrogen bonding
d. London dispersion and dipole-dipole
London dispersion forces (also called as induced dipole – induced dipole interactions), exist because of the generation of temporary polarity due to collision of particles and for this very reason, they are present in all molecules and inert gases as well.
Because of the presence of a permanent dipole, there will be dipole-dipole interactions present here.
There is no H that is directly attached to an oxygen atom, so H-bonding cannot be present.
v̅ = RH [ (1/n12) – (1/n22)]
The correct statements among (A) to (D) are:
A) The integer n1= 2.
B) The ionization energy of hydrogen can be calculated from the wave number of these lines.
C) The lines of longest wavelength corresponds to n2= 3.
D) As wavelength decreases, the lines of the series converge.
a. B, C, D
b. A, B, D
c. A, C, D
d. A, B, C
- is correct since the series studied in H-spectrum, including Balmer series, are de-excitation series or emission series. So, electrons get de-excited to n= 2 which means that nlower= 2.
- It is possible to obtain I.E. from the formula above, but since the question has stated the formula for the Balmer series, nlower has been fixed as 2. So, it is not possible to calculate I.E. from it. To calculate I.E., we’ll have to put nlower= 1, which isn’t possible here.
- ΔE = hc/λ
With nlower fixed as 2, ΔE increases as nhigher is increased. So, the last line of the Balmer series,i.e. from infinity to n= 2, will have the maximum energy in the series and thus, the lowest wavelength. Similarly, the first line in the series, i.e. from n= 3 to n= 2 will have the lowest energy in the series and thus, the highest wavelength. Which makes this statement correct. - As orbits with higher orbit number or those that are further away from the nucleus are considered, the energy gap in-between subsequent orbits decrease. Now, consider the following for example and with nlower fixed as 2.
Energy of a photon released on transition from n= 100 to n= 2 will have similar energy to that of the photon that gets released on transition from n= 101 to n= 2, because energy of the 100th and the 101th orbit will be very close in value. That means they will also have very close values of wavelengths, which further implies that these two lines will be situated quite close to each other on the photographic plate.
In a similar fashion, we can see that as the nhigher increases, the lines start to converge together. And since, increasing the nhigher will indeed lead to an increase in the energy of the photon released, it will end up releasing photons of shorter wavelengths. Combining these two statements we can easily see that as the wavelength decreases, the spectral lines start to converge.
a. 496, 737, 577, 786
b. 496, 577, 737, 786
c. 496, 577, 786, 737
d. 786, 737, 577, 496
The expected order is Na < Mg < Al < Si.
But the actual/experimental order turns out to be Na < Al < Mg < Si, because of the fully filled s- sub shell of magnesium and the s2p1 configuration of Al which makes it relatively easy for Al to lose its outermost electron.
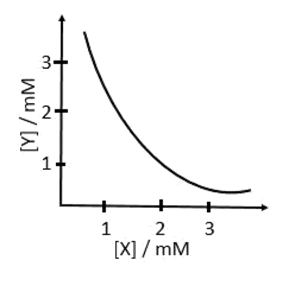
a. X2Y, 2 x 10−9M3
b. XY2, 1 x 10−9M3
c. XY2, 4 x 10−9M3
d. XY, 2 x 10−6M3
(a) X2Y(s) ⇌ 2X+ + Y2−
Ksp = [X+]2[Y2−] = 4 × 10−6 × 10−3 = 4 × 10−9
(b) XY2(s) ⇌ X2+ + 2Y−
Ksp = [X2+][Y−]2 = 10−3 × 4 × 10−6 = 4 × 10−9
(c) XY2(s) ⇌ X2+ + 2Y−
Ksp = [X2+][Y−]2 = 10−3 × ( 2 × 10−3)2 = 4 × 10−9
(d) XY(s) ⇌ X+ + Y−
Ksp = [X+][Y−] = 10−3 × 10−3 = 10−6
a. [Co(NO2)3(NH3)3]
b. [PtCl2(NH3)2
c. [Co(NH3)4Cl2]
d. [CoCl2(en)2]
Facial and meridional geometrical isomerism is observed only in [MA3B3] type complexes which is given in option a.
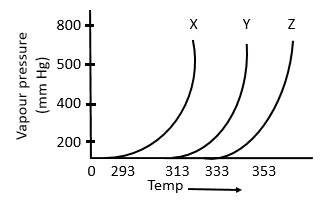
The following inferences are made:
A) X has higher intermolecular interactions compared to Y
B) X has lower intermolecular interactions compared to Y
C) Z has lower intermolecular interactions compared to Y The correct inference(s) is/are:
a. C
b. A
c. B
d. A and C
As shown in the plot below, for the same T, the vapour pressure of X is the highest and of Z is the lowest. Now, that means with the same average K.E. of X, Y and Z molecules, the X molecules are able to compensate their respective intermolecular forces better. So, X molecules have the highest vapour pressure. This implies that the intermolecular forces in X are the weakest among the three. The opposite could be said for Z as well.

a. AlCl3 > K3[Fe(CN)6] > K2CrO4 > KBr = KNO3
b. K3 [Fe(CN)6 ] < K2CrO4 < AlCl3 < KBr < KNO3
c. K3 [Fe(CN)6 ] < K2CrO4 < KBr = KNO3 = AlCl3
d. K3 [Fe(CN)6 ] > AlCl3 > K2CrO4 > KBr > KNO3
The minimum concentration of an electrolyte which is required to cause the coagulation or flocculation of a sol is known as flocculation value. Flocculation value is inversely proportional to coagulation power (coagulation power is directly proportional to the valency of the ions causing coagulation). Fe(OH)3 sol is a positive sol and thus we have to consider the valency of the anions in the given electrolytes.
a. − 6RT
b. – 6 × 2.303 RT
c. + 6RT
d. +6 × 2.303 RT
K1 = Ae−Ea1/RT ….(1)
K2 = Ae−Ea2/RT ….(2)
Dividing equation 1 with equation 2, we get
K1/K2 = e (Ea2−Ea1)/RT
10−6 = e (Ea2−Ea1)/RT
Taking loge on both sides, we get
∆E = Ea2 − Ea1 = – 6 × 2.303 RT
a. CaSO4. 1/2 H2O
b. Dead burnt plaster
c. CaSO4 5H2O
d. Anhydrous CaSO4
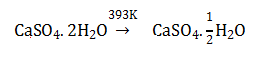
a. Mn
b. Co
c. Ni
d. Fe
Consider an element E
E2+ → E3+ would be the 3rd I.E. of the element E.
Electronic configuration of Mn is [Ar]4s23d5, Co is [Ar]4s23d7, Fe is [Ar]4s23d6, Ni is [Ar]4s23d8
Electronic configuration of Mn2+ is [Ar]3d5, Co2+ is [Ar]3d7, Fe2+ is [Ar]3d6, Ni2+ is [Ar]3d8
As it is evident from the above configurations of the E2+ for the given elements, Fe2+ would require the least amount of energy for removal of electron as it has the configuration 3d6 4s0. That means that its E3+ form is the most stable among the four elements provided in their respective E3+ states, i.e., when compared, the next electron removal will require least amount of energy.
a. Aq. NaOH in a pipette and aqueous oxalic acid in a burette
b. Aq. NaOH in a volumetric flask and concentrated H2SO4 in a conical flask
c. Aq. NaOH in a burette and concentrated H2SO4 in a conical flask
d. Aq. NaOH in a burette and aqueous oxalic acid in a conical flask
The standard solution is usually kept in burette. The oxalic acid is a primary standard solution while H2SO4 is a secondary standard solution.
a. B > A > D > C
b. B > D > C > A
c. B > D > A > C
d. D > B > C > A
In E1mechanism, the rate determining step is formation of carbocation. So, stability of carbocation formed decides the rate. In option D, the cation formed is resonance stabilised. In option C, the cation formed is a 2 o carbocation. In option A and B, the carbocations formed are 1 o but there is a chance of rearrangement in option b and after the rearrangement, the carbocation formed in option b will be allylic. So, the order of reaction is as follows: D > B > C > A.
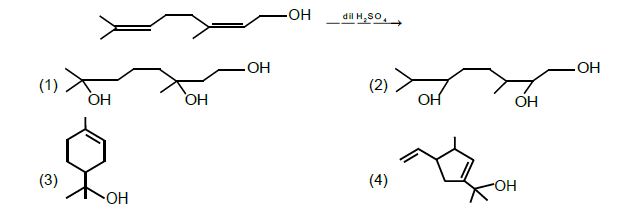
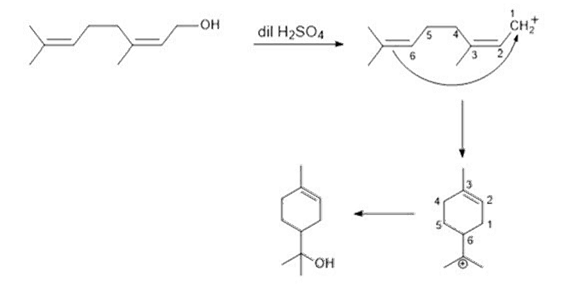
a. Phenol < methanol < p-ethoxyphenol
b. methanol < p-ethoxyphenol < phenol
c. Phenol < p-ethoxyphenol < methanol
d. methanol < phenol < p-ethoxypheno
In methanol, there is no resonance. In phenol, there is resonance. In p-Ethoxyphenol, there is resonance involved but the involvement of lone pair of oxygen in OH group is poor as compared with phenol due to the presence of lone pair oxygen in OCH3 group which are also involved in resonance. So, partial double bond character develops in C—OH bond of phenol and p-ethoxyphenol but in case of p-ethoxyphenol, resonance is poor as compared to phenol. So, bond length follows the order: methanol > p-ethoxyphenol > phenol
i. 𝐶𝑂2
ii. 𝐻2𝑂
iii. 𝐶𝐹𝐶
iv. 𝑂2
v. 𝑂3
a. i, ii iii and iv
b. i, iii, iv and v
c. i and iv
d. i, ii, iii and v
𝐶𝑂2, 𝑂3, 𝐻2𝑂 vapours and 𝐶𝐹𝐶′𝑠 are green house gases.



a. Fractional distillation, isohexane
b. Simple distillation, 3-methylpentane
c. Fractional distillation, 3-methylpentane
d. Simple distillation, isohexane
When the difference between the B.P. of the two liquids is less than around 40 𝑜𝐶, fractional distillation is more efficient. The difference between the boiling points of isohexane and 3-methylpentane is only 3 degrees. So, fractional distillation is the best suitable method. Since, isohexane has a lower boiling point, it comes out first.
a. The pentacetate glucose does not react with hydroxylamine to give oxime
b. Glucose reacts with hydroxylamine to form oxime.
c. Glucose gives Schiff’s test for aldehyde.
d. Glucose exists in two crystalline forms alpha and beta.
Glucose exists in two crystalline forms alpha and beta which are anomers of each other.
Glucose does not react with Schiff’s reagent because after the internal cyclisation, it forms either alpha- anomer or beta-anomer. In these forms, free aldehydic group is not present.
Glucose forms open chain structure in aqueous solution which contains aldehyde at chain end. This aldehydic group reacts with NH4OH to form oxime. On the other hand, glucose penta acetate being a cyclic structure even in aqueous form does not have terminal carbonyl group. Therefore it will not react with 𝑁𝐻4𝑂𝐻.
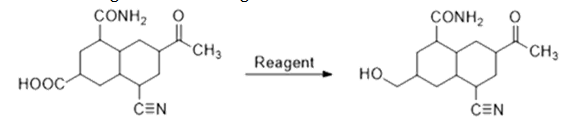
a. 𝐵2𝐻6
b. 𝐿𝑖𝐴𝑙𝐻4
c. 𝑁𝑎𝐵𝐻4
d. 𝐻2, 𝑃𝑑
𝐵2𝐻6 does not reduce amide, carbonyl group and cyanide. It selectively reduces carboxylic acid to alcohol. So, for this conversion, it is the best suitable reagent.
𝑀𝐴𝑔𝑁𝑂3 = 169.87 g/mpl
To react completely with one mole of [𝑀𝐿6]𝑙3 , 3 moles of 𝐴𝑔𝑁𝑂3 is required.
0.3 g [𝑀𝐿6 ]𝑙3 means (0.3/267.46) moles of [𝑀𝐿6 ]𝐶𝑙3.
So, moles of 𝐴𝑔𝑁𝑂3 required will be (0.3×3)/267.46 moles
To find the volume, (0.3×3)/267.46 = 0.125× (𝐿)
(𝐿) = 0.02692
(𝑚𝐿) = 26.92
2𝐻2𝑂 → 𝑂2 + 4𝐻+ + 4𝑒–; 𝐸° = – 1.23 𝑉
(R=8.314 J mol-1K-1; temp.=298 K; oxygen under std. atm. Pressure of 1 bar.)
2𝐻2𝑂 → 𝑂2 + 4𝐻+ + 4𝑒–; 𝐸° = – 1.23 𝑉

10 ppm of Fe means 10 g of Fe in 106 g of wheat. So, for 100 kg i.e.,105 g of wheat. 𝐹𝑒 needed is 1 g. So, for 1 g of Fe, the mass of 𝐹𝑒𝑆𝑂4. 7𝐻2𝑂 required is 278/56 = 4.96 g.
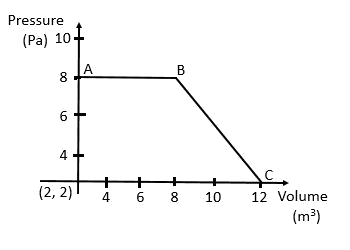
Work done by the gas
= The area under the curve
= (Area of the square) + (Area of the triangle)
= 48 J
The structure of penicillin is shown below:

So, the number of chiral centers= 3
Video Lessons – January 8 Shift 1 Chemistry




JEE Main 2020 Chemistry Paper January 8 Shift 1














Comments