JEE Main 2020 Paper with Solutions Physics – Shift 1- 8th January is given here. Students are recommended to practise these questions so that they can improve their accuracy and problem-solving skills. The questions and solutions can be accessed from our page directly. The PDF format is also available which can be downloaded easily. Ultimately, students will be able to face the exam with a better confidence level.
JEE Main 2020 Question Papers
January 8 Shift 1 – Physics
1. A particle of mass 𝑚 is fixed to one end of a light spring having force constant k and unstretched length l. The other end is fixed. The system is given an angular speed 𝜔 about the fixed end of the spring such that it rotates in a circle in gravity free space. Then the stretch in the spring is
a. ℓ m 𝜔2/(k-m 𝜔2)
b. ℓ m 𝜔2/(k+m 𝜔2)
c. ℓ m 𝜔2/(k-m 𝜔)
d. ℓ m 𝜔2/(k+m 𝜔)
The centripetal force is provided by the spring force.
mω2(ℓ + x) = kx
kx = m(ℓ + x)ω2
x = mℓω2 /( k – mω2)

2. Three charged particles A, B and, C with charge -4q, +2q and -2q are present on the circumference of a circle of radius 𝑑. The charges particles A, C and centre O of the circle formed an equilateral triangle as shown in figure. Electric field at O along x- direction is:
 a. √3q/4πƐ0d2
b. 2√3q/πƐ0d2
c. √3q/πƐ0d2
d. 3√3q/4πƐ0d2
a. √3q/4πƐ0d2
b. 2√3q/πƐ0d2
c. √3q/πƐ0d2
d. 3√3q/4πƐ0d2
Applying superposition principle,
\(\begin{array}{l}\vec{E_{net}} = \vec{E_{1}}+\vec{E_{2}}+\vec{E_{3}}\end{array} \)

By symmetry, net electric field along the x-axis.
\(\begin{array}{l}\left | \vec{E_{net}} \right | = \frac{4kq}{d^{2}}\times 2\cos 30^{0} = \frac{\sqrt{3}q}{\pi \varepsilon _{0}d^{2}}\end{array} \)
3. A thermodynamic cycle xyzx is shown on a V- T diagram .

The P-V diagram that best describes this cycle is : (Diagrams are schematic and not upto scale)

For the given V – T graph
For the process x → y; V ∝ T; 𝑃 =constant.
For the process y → z; V =constant
Only ′𝑐′ satisfies these two conditions.
4. Find the co-ordinates of center of mass of the lamina shown in the figure below.
 a. (0.75 m, 1.75 m)
b. (0.75 m, 0.75 m)
c. (1.25 m, 1.5 m)
d. (1 m, 1.75 m)
a. (0.75 m, 1.75 m)
b. (0.75 m, 0.75 m)
c. (1.25 m, 1.5 m)
d. (1 m, 1.75 m)
The Lamina can be divided into two parts having equal mass 𝑚 each.

\(\begin{array}{l}\vec{r}_{cm} = \frac{m\times (\frac{\hat{i}}{2}+j)+m\times(\hat{i}+\frac{5\hat{j}}{2} )}{2m}\end{array} \)
\(\begin{array}{l}\vec{r}_{cm} = \frac{3}{4}\hat{i}+\frac{7}{4}\hat{j}\end{array} \)
5. The plot that depicts the behavior of the mean free time 𝜏 (time between two successive collisions) for the molecules of an ideal gas, as a function of temperature (T), qualitatively, is: (Graph are schematic and not drawn to scale)

τ ∝ 1/√T
6. Effective capacitance of parallel combination of two capacitors 𝐶1 and 𝐶2 is 10 μF. When these capacitor are individually connects to a voltage source of 1 𝑉, the energy stored in the capacitor 𝐶2 is 4 times of that in 𝐶1. If these capacitors are connected in series, their effective capacitance will be:
a. 1.6 μF
b. 3.2 μF
c. 4.2 μF
d. 8.4 μF

Given that,
C1 + C2 = 10 μF …(i)
4( ½ C1V2) = ½ C2V2
4C1 = C2 …(ii)
From equations (i) and (ii)
C1 = 2 μF
C2 = 8 μF
If they are in series
Ceq = C1C2/(C1+ C2)
= 1.6 μF
7. Consider a uniform rod of mass 4𝑚 and length 𝐿 pivoted about its centre. A mass 𝑚 is moving with a velocity 𝑣 making angle θ=π/4 to the rod’s long axis collides with one end of the rod and stick to it. The angular speed of the rod-mass system just after collision is
a. 3√2𝑣/7L
b. 4𝑣/7L
c. 3𝑣/7√2L
d. 3𝑣/7L

There is no external torque on the system about the hinge point. So,
\(\begin{array}{l}\vec{L_{1}} = \vec{L_{f}}\end{array} \)
\(\begin{array}{l}\frac{mv}{\sqrt{2}}\times \frac{1}{2} = \left [ \frac{4mL^{2}}{12} +\frac{mL^{2}}{4}\right ]\times \omega\end{array} \)
= 6𝑣/7√2L = 3√2 𝑣/7L
8. When photons of energy 4 eV strikes the surface of a metal A, the ejected photoelectrons have maximum kinetic energy 𝑇𝐴 eV and de-Broglie wavelength 𝜆𝐴. The maximum kinetic energy of photoelectrons liberated from another metal B by photon of energy 4.50 eV is 𝑇𝐵 = (𝑇𝐴 − 1.5) eV. If the de-Broglie wavelength of these photoelectrons 𝜆𝐵 = 2𝜆𝐴, then the work function of metal B is
a. 3 eV
b. 1.5 eV
c. 2 eV
d. 4 eV
\(\begin{array}{l}\lambda = \frac{h}{\sqrt{2(KE)m_{B}}}\end{array} \)
= ∝ 1/√KE
\(\begin{array}{l}\frac{\lambda _{A}}{\lambda _{B}} = \frac{\sqrt{KE_{B}}}{\sqrt{KE_{A}}}\end{array} \)
\(\begin{array}{l}\frac{1}{2} = \sqrt{\frac{T_{A}-1.5}{T_{A}}}\end{array} \)
TA = 2eV
KEB = 2 – 1.5 = 0.5 eV
∅B = 4.5 – 0.5 = 4 eV
9. The length of a potentiometer wire of length 1200 𝑐𝑚 and it carries a current of 60 𝑚𝐴. For a cell of emf 5 𝑉 and internal resistance of 20Ω, the null point on it is found to be at 1000 𝑐𝑚. The resistance of whole wire is
a. 80Ω
b. 100Ω
c. 120Ω
d. 60Ω

Let Resistance per unit length of potentiometer wire = λ
⇒ λ × 1000 × 60 × 10<sup>-3</sup> = 5
⇒ λ 5 / 60
Resistance of potentiometer wire = 1200 × 5 / 60 = 100Ω
10. The magnifying power of a telescope with tube length 60 cm is 5. What is the focal length of its eyepiece?
a. 10 cm
b. 20 cm
c. 30 cm
d. 40 cm
m = f0/fe = 5
f0 = 5fe
f0 + fe = 5fe + fe = 6fe = length of the tube
6fe = 60 cm
fe = 10 cm
11. Consider two solid spheres of radii 𝑅1= 1 m, 𝑅2 = 2 m and masses M1 & M2, respectively. The gravitational field due to two spheres 1 and 2 are shown. The value of M1/M2 is
 a. 1/6
b. 1/3
c. 1/2
d. 2/3
a. 1/6
b. 1/3
c. 1/2
d. 2/3
Gravitation field will be maximum at the surface of a sphere. Therefore,
GM2/22 = 3 and GM1/12 = 2
(M2/M1)× ¼ = 3/2
M1/M2 = 1/6
12. Proton with kinetic energy of 1 MeV moves from south to north. It gets an acceleration of 1012 m/s2 by an applied magnetic field (west to east). The value of magnetic field: (Rest mass of proton is 1.6 × 10−27 kg)
 a. 0.71 mT
b. 7.1 mT
c. 71 mT
d. 0.071 mT
a. 0.71 mT
b. 7.1 mT
c. 71 mT
d. 0.071 mT
K. E = 1 × 106 eV = 1.6 × 10−13 J
= ½ mev2
Where me is the mass of the electron = 1.6×10 -27
1.6 × 10-13 = ½ × 1.6 × 10-27 × v2
v = √2×107 m/s
Bqv = mea
B = (1.6 ×10 -27 × 1012 )/ (1.6×10-19×√2× 107)
= 0.71 × 10-3 T
= 0.71 mT
13. If finding the electric field around a surface is given by \(\begin{array}{l}\left | \vec{E} \right | = \frac{q_{enclosed}}{\varepsilon_{0} \left | A \right |}\end{array} \)
is applicable. In the formula Ɛ0 is permittivity of free space, A is area of Gaussian and 𝑞𝑒𝑛𝑐 is charge enclosed by the Gaussian surface. This equation can be used in which of the following equation?
a. Only when the Gaussian surface is an equipotential surface.
b. Only when \(\begin{array}{l}\left | \vec{E} \right |\end{array} \)
= constant on the surface.
c. Equipotential surface and \(\begin{array}{l}\left | \vec{E} \right |\end{array} \)
is constant on the surface
d. for any choice of Gaussian surfaces.
The magnitude of the electric field is constant and the electric field must be along the area vector i.e. the surface is equipotential.
14. The dimension of stopping potential 𝑉0 in photoelectric effect in units of Planck’s constant (h), speed of light (c), and gravitational constant (G) and Ampere (A) is
a. h2/3 c5/3 G1/3 A−1
b. h2c1/3G3/2A−1
c. h0 G -1 c 5 A−1
d. h−2/3 c−1/3 G4/3 A−1
V = K(h)a(I)b(G)c(c)d
Unit of stopping potential is (V0) Volt.
We know [h] = ML2T−1
[I] = A
[G] = M−1L3T−2
[C] = LT−1
[V] = ML2T−3A−1
ML2T−3A−1 = (ML2T−1)a(A)b (M−1L3T−2)c(LT−1)d
ML2T-3A-1 = Ma-cL2a+3c+dT−a−2c−dAb
a – c = 1
2a + 3c + d = 2
-a – 2c – d = -3 b = -1
On solving,
c = -1
a = 0
d = 5
b = -1
V = K(h)0(A)−1(G)−1(c)5
15. A leak proof cylinder of length 1 m, made of metal which has very low coefficient of expansion is floating in water at 0o C such that its height above the water surface is 20 cm. When the temperature of water is increases to 4o C, the height of the cylinder above the water surface becomes 21 cm. The density of water at T = 4o C relative to the density at T = 0o C is close to
a. 1.01
b. 1.03
c. 1.26
d. 1.04

Since the cylinder is in equilibrium, it’s weight is balanced by the Buoyant force.
mg = A(80)(ρ0oc)g
mg = A(79)(ρ4oc)g
ρ4oc/ ρ0oc = 80/79 = 1.01
16. The graph which depicts the result of Rutherford gold foil experiment with α- particle is:
𝜃: Scattering angle
𝑁 ∶ Number of scattered 𝛼 − particles is detected
(Plots are schematic and not to scale)
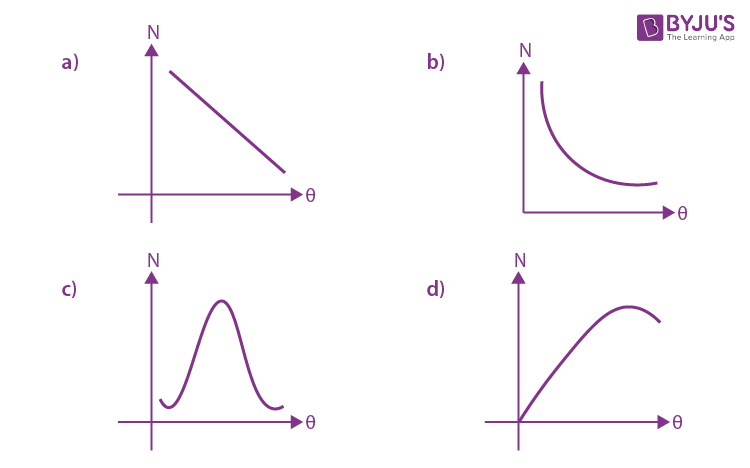

N ∝ 1/sin4(θ/2)
17. At time t = 0 magnetic field of 1000 Gauss is passing perpendicularly through the area defined by the closed loop shown in the figure. If the magnetic field reduces linearly to 500 Gauss, in the next 5 s, then induced EMF in the loop is:
 a. 56 μV
b. 28 μV
c. 30 μV
d. 48 μV
a. 56 μV
b. 28 μV
c. 30 μV
d. 48 μV
\(\begin{array}{l}\epsilon =\left | \frac{-d\phi }{dt} \right | = \left | \frac{-A\: dB }{dt} \right |\end{array} \)
\(\begin{array}{l}(16\times 4-4\times 2)\frac{(1000-500)}{5}\times 10^{-4}\times 10^{-4}\end{array} \)
= 56×500×10-8/5
= 56× 10-6 V
18. Choose the correct Boolean expression for the given circuit diagram:
 a. A.B
b. A + B
c.
a. A.B
b. A + B
c. \(\begin{array}{l}\bar{A}+ \bar{B}\end{array} \)
d. \(\begin{array}{l}\bar{A}. \bar{B}\end{array} \)
First part of figure shown OR gate and second part of figure shown NOT gate.
So, Y =
\(\begin{array}{l}\bar{A}. \bar{B}\end{array} \)
19. Consider a solid sphere of density ρ(r) = ρ0 (1- r2/R2), 0< r ≤ R. The minimum density of a liquid in which it float is just
a. (2/5) ρ0
b. (2/3) ρ0
c. ρ0/5
d. ρ0/3
Let the mass of the sphere be m and the density of the liquid be ρL
ρ = ρ0 ( 1 – r2/R2), 0< r ≤ R
Since the sphere is floating in the liquid, buoyancy force (FB) due to liquid will balance the weight of the sphere.
𝐹 = mg
ρL (4π/3) R3g = ∫ρ(4πr2 dr)g
ρL (4π/3) R3 = ∫ ρ0 ( 1 – r2/R2) 4πr2dr
ρL (4/3)π R3 =
\(\begin{array}{l}\int_{0}^{R}\rho _{0}4\pi (r^{2}-\frac{r^{4}}{R^{2}})dr= \rho _{0}4\pi\left ( \frac{r^{3}}{3} -\frac{r^{5}}{5R^{2}}\right )_{0}^{R}\end{array} \)
ρL = (2/5) ρ0
20. The critical angle of a medium for a specific wavelength, if the medium has relative permittivity 3 and relative permeability 4/3 for this wavelength, will be
a. 15°
b. 30°
c. 45°
d. 60°
If the speed of light in the given medium is V then,
V = 1/√(μƐ)
We know that, n = c/v
n = √(μr Ɛr) = 2
sin θc = ½
θc = 300
21. A body of mass 𝑚=0.10 𝑘𝑔 has an initial velocity of \(\begin{array}{l}3\hat{i}\end{array} \)
𝑚/𝑠. It collides elastically with another body, B of the mass which has an initial velocity of \(\begin{array}{l}5\hat{j}\end{array} \)
𝑚/𝑠. After collision, A moves with a velocity \(\begin{array}{l}v= 4(\hat{i}+\hat{j})\end{array} \)
𝑚/𝑠. The energy of B after collision is written as (𝑥/10) 𝐽, the value of 𝑥 is
Mass of each object, 𝑚1= 𝑚2 = 0.1 𝑘𝑔
Initial velocity of 1st object, 𝑢1=5 𝑚/𝑠
Initial velocity of 2nd object, 𝑢2 =3 𝑚/𝑠
Final velocity of 1st object, 𝑉1=
\(\begin{array}{l}v= 4\hat{i}+4\hat{j}\end{array} \)
𝑚/𝑠 =√(42+42 )= 16√2 𝑚/𝑠
For elastic collision, kinetic energy remains conserved
Initial kinetic energy (Ki) = final kinetic energy (Kf)
½ mu12 + ½ mu22 = ½ mV12 + ½ mV22
½ m(5)2 + ½ m(3)2 = ½ m(16√2)2 + ½ mV22
V2 = √2 m/s
Kinetic energy of second object = ½ mV22
= ½ × 0.1 × √22
= 0.1
= 1/10 J
x = 1
22. A point object in air is in front of the curved surface of a plano-convex lens. The radius of curvature of the curved surface is 30 cm and the refractive index of lens material is 1.5, then the focal length of the lens (in cm) is
Applying Lens makers’ formula,
1/f = (μ – 1)[(1/R1) – (1/R2)]
R1 =∞
R2 = -30 cm
μ = 1.5
1/f = (1.5 – 1)[(1/∞) – (1/-30)]
1/f = 0.5/30
f = 60 cm
23. A particle is moving along the x-axis with its coordinate with time t given by x(t) = -3t2 + 8t + 10 𝑚. Another particle is moving along the y-axis with its coordinate as a function of time given by y = 5 – 8t3 m. At t = 1 s, the speed of the second particle as measured in the frame of the first particle is given as √v . Then v (m/s) is
x = −3t2 + 8t + 10
\(\begin{array}{l}\vec{V_{A}}\end{array} \)
= (−6t + 8)\(\begin{array}{l}\hat{i}\end{array} \)
= 2
\(\begin{array}{l}\hat{i}\end{array} \)
y = 5 − 8t3
\(\begin{array}{l}\vec{V_{B}}\end{array} \)
= −24t2 \(\begin{array}{l}\hat{j}\end{array} \)
\(\begin{array}{l}\left | \overrightarrow{V_{B/A}} \right | = \left | \overrightarrow{V_{B}} -\overrightarrow{V_{A}} \right | = \left | -24\hat{j} -2\hat{i}\right |\end{array} \)
v = √(242 + 22)
v = 580 m/s
24. A one metre long (both ends open) organ pipe is kept in a gas that has double the density of air at STP. Assuming the speed of sound in air at STP is 300 m/s, the frequency difference between the fundamental and second harmonic of this pipe is __Hz.
V = √(B/ρ)
Vpipe/ Vair =
\(\begin{array}{l}\sqrt{\frac{\frac{B}{2\rho }}{\frac{B}{\rho }}}= \frac{1}{\sqrt{2}}\end{array} \)
Vpipe = Vair/√2
fn = Vpipe(n+1)/2l
f1-f0 = Vpipe/ 2l
= 300/2√2
= 106.06 Hz ( if √2 = 1.414) ≈ 106 Hz
25. Four resistors of resistance 15 Ω, 12 Ω, 4Ω and 10Ω respectively in cyclic order to form a wheatstone’s network. The resistance that is to be connected in parallel with the resistance of 10 to balance the network is __.

[(10R)/(10+R) ]×12 = 15 ×4
R = 10Ω
Download PDF Here








































Comments