The JEE Main 2022 July 26 – Shift 1 Maths Question Paper with Solutions is given on this page. Students can solve the JEE Main 2022 question papers so as to enhance their performance in the upcoming exams. Practising the JEE Main 2022 question paper with solutions will also help students to boost their speed of problem-solving. Students can use the JEE Main 2022 answer keys to find out accurate answers to the JEE questions.
JEE Main 2022 26th July Morning Shift Question Paper – Maths with Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. Let f :R→R be a continuous function such that f(3x) – f(x) = x. If f(8) = 7, then f(14) is equal to
(A) 4
(B) 10
(C) 11
(D) 16
Answer (B)
Sol.
\(\begin{array}{l}f\left(3x\right) – f\left(x\right) = x …(1)\\x\rightarrow\frac{x}{3} \end{array} \)
\(\begin{array}{l} f\left(x\right)-f\left(\frac{x}{3}\right)=\frac{x}{3}\cdots(2)\end{array} \)
\(\begin{array}{l} \text{Again}~ x\rightarrow\frac{x}{3}\end{array} \)
\(\begin{array}{l} f\left(\frac{x}{3}\right)-f\left(\frac{x}{9}\right)=\frac{x}{3^2}\cdots(3)\end{array} \)
\(\begin{array}{l}\text{Similarly}~ f\left(\frac{x}{3^{n-2}}\right)-f\left(\frac{x}{3^{n-1}}\right)=\frac{x}{3^{n-1}}\cdot\cdot\cdot\cdot\cdot\cdot\cdot\left(n\right)\end{array} \)
Adding all these and applying n→∞
\(\begin{array}{l} \displaystyle \lim_{n \to \infty}\left(f\left(3x\right)-f\left(\frac{x}{3^{n-1}}\right)\right)=x\left(1+\frac{1}{3}+\frac{1}{3^2}+\cdots\right)\end{array} \)
\(\begin{array}{l} f\left(3x\right)-f\left(0\right)=\frac{3x}{2} \end{array} \)
\(\begin{array}{l} \text{ Putting } x=\frac{8}{3}\end{array} \)
f(8) – f(0) = 4
⇒ f(0) = 3
\(\begin{array}{l} \text{ Putting } x=\frac{14}{3}\end{array} \)
\(\begin{array}{l}f\left(14\right) – 3 = 7\Rightarrow f\left(14\right) = 10\end{array} \)
2. Let O be the origin and A be the point z1 = 1 + 2i. If B is the point z2, Re(z2) < 0, such that OAB is a right angled isosceles triangle with OB as hypotenuse, then which of the following is NOT true?
\(\begin{array}{l}\left(A\right) argz_2 = \pi – tan^{-1}3\end{array} \)
\(\begin{array}{l} (\text{B})\ (\text{arg})\left(z_1-2z_2\right)=-\tan^{-1}\frac{4}{3}\end{array} \)
\(\begin{array}{l} (\text{C})\ \left|z_2\right|=\sqrt{10}\end{array} \)
\(\begin{array}{l} (\text{D})\ \left|2z_1-z_2\right|=5\end{array} \)
Answer (D)
Sol.
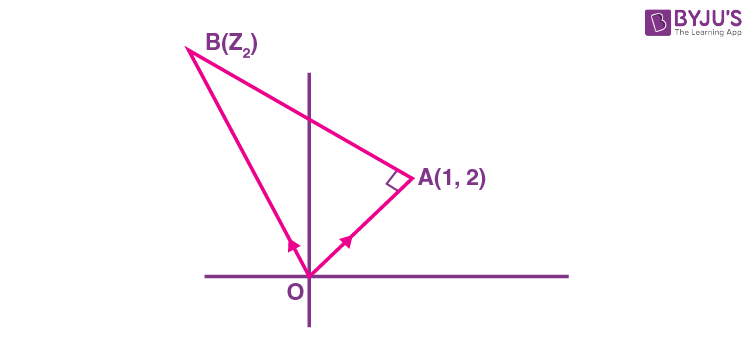
\(\begin{array}{l} \frac{z_2-0}{\left(1+2i\right)-0}=\frac{\left|OB\right|}{\left|OA\right|}e^\frac{i\pi}{4}\end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{z_2}{1+2i}=\sqrt{2}e^\frac{i\pi}{4}\end{array} \)
\(\begin{array}{l}\text{OR}~ z_2 = \left(1 + 2i\right)\left(1 + i\right) = -1 + 3i\\ arg~ z_2 = \pi – tan^{-1}3\end{array} \)
\(\begin{array}{l} \left|z_2\right|=\sqrt{10}\end{array} \)
\(\begin{array}{l}z_1 – 2z_2 = \left(1 + 2i\right) + 2 – 6i = 3 – 4i\end{array} \)
\(\begin{array}{l} \text{arg}\left(z_1-2z_2\right)=-\tan^{-1}\frac{4}{3} \end{array} \)
\(\begin{array}{l} \left|2z_1-z_2\right|=\left|2+4i+1-3i\right|=\left|3+i\right| \end{array} \)
\(\begin{array}{l} =\sqrt{10}\end{array} \)
3. If the system of linear equations.
8x + y + 4z = –2
x + y + z = 0
\(\begin{array}{l}\lambda x – 3y = \mu\end{array} \)
has infinitely many solutions, then the distance of the point (λ, μ, -1/2) from the plane 8x + y + 4z + 2 = 0 is
\(\begin{array}{l} (\text{A})\ 3\sqrt{5}\end{array} \)
\(\begin{array}{l}\left(B\right) 4\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{26}{9}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{10}{3}\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l} \Delta =\begin{vmatrix}8 & 1 & 4 \\1 & 1 & 1 \\\lambda & -3 & 0 \\\end{vmatrix} \end{array} \)
\(\begin{array}{l}= 8\left(3\right) -1\left(-\lambda\right)+4\left(-3-\lambda\right) \end{array} \)
\(\begin{array}{l}= 24 + \lambda – 12 – 4\lambda\\ = 12 – 3\lambda\end{array} \)
So for λ = 4, it is having infinitely many solutions.
\(\begin{array}{l} \Delta_x=\begin{vmatrix}-2 & 1 & 4 \\0 & 1 & 1 \\\mu & -3 & 0 \\\end{vmatrix}\end{array} \)
\(\begin{array}{l}= -2(3) -1(-\mu) + 4(-\mu)\\ = -6 – 3\mu = 0\end{array} \)
For μ= –2
\(\begin{array}{l}\text{Distance of} \left (4, -2, \frac{-1}{2}\right) \text{from}~8x + y + 4z + 2 = 0\end{array} \)
\(\begin{array}{l} =\frac{32-2-2+2}{\sqrt{64+1+16}}=\frac{10}{3}\textup{ units} \end{array} \)
4. Let A be a 2 × 2 matrix with det (A) = –1 and det((A + I) (Adj (A) + I)) = 4. Then the sum of the diagonal elements of A can be
(A) -1
(B) 2
(C) 1
(D) -√2
Answer (B)
Sol.
\(\begin{array}{l}\left|\left(A + I\right)\left(adj~A + I\right)\right| = 4\\ \Rightarrow \left|Aadj~A + A + adj~A + I\right| = 4\\ \Rightarrow \left|\left(A\right)I + A + adj~A + I\right| = 4\end{array} \)
\(\begin{array}{l}\left|A\right| = -1\Rightarrow \left|A + adj~A\right| = 4\end{array} \)
\(\begin{array}{l} A=\begin{bmatrix}a & b \\c & d \\\end{bmatrix}adj\ A=\begin{bmatrix}a & -b \\-c & d \\\end{bmatrix}\end{array} \)
\(\begin{array}{l} \Rightarrow\ \begin{vmatrix}\left(a+d\right) & 0 \\0 & \left(a+d\right) \\\end{vmatrix}=4\end{array} \)
⇒ a + d = ±2
5. The odd natural number a, such that the area of the region bounded by y = 1, y = 3, x = 0, x = ya is 364/3, is equal to
(A) 3
(B) 5
(C) 7
(D) 9
Answer (B)
Sol. a is a odd natural number and
\(\begin{array}{l} \left|\displaystyle\int\limits_1^3y^ady\right|=\frac{364}{3}\end{array} \)
\(\begin{array}{l} \Rightarrow\ \left|\frac{1}{a+1}\left(y^{a+1}\right)_1^3\right|=\frac{364}{3}\end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{3^{a+1}-1}{a+1}=\pm\frac{364}{3}\end{array} \)
Solving with (+) sign,
\(\begin{array}{l} \frac{3^{a+1}-1}{a+1}=\frac{364}{3}\Rightarrow \left(a=5\right)\end{array} \)
Solving with (-) sign,
\(\begin{array}{l}\frac{3^{a+1}-1}{a+1}=\frac{-364}{3}, \text{No}~a\text{ exist}\\ \therefore (a = 5)\end{array} \)
6. Consider two G.Ps. 2, 22, 23, …. and 4, 42, 43, … of 60 and n terms respectively. If the geometric mean of all the 60 + n terms is \(\begin{array}{l} \left(2\right)^\frac{225}{8}\ \text{then}\ \sum_{k=1}^{n}k\left(n-k\right)\end{array} \)
is equal to
(A) 560
(B) 1540
(C) 1330
(D) 2600
Answer (C)
Sol. Given G.P′s 2, 22, 23, … 60 terms
4, 42, … n terms
\(\begin{array}{l}\text{Now,}~\text{GM}=2^\frac{225}{8} \end{array} \)
\(\begin{array}{l} \left(2.2^2\cdots 4.4^2\cdots\right)^\frac{1}{60+n}=2^\frac{225}{8}\end{array} \)
\(\begin{array}{l} \left(2^\frac{n^2+n+1830}{60+n}\right)=2^\frac{225}{8}\end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{n^2+n+1830}{60+n}=\frac{225}{8}\end{array} \)
\(\begin{array}{l} \Rightarrow 8n^2 – 217n + 1140 = 0\end{array} \)
\(\begin{array}{l} n=\frac{57}{8},20,\text{ so }n=20 \end{array} \)
\(\begin{array}{l} \therefore \sum_{k=1}^{20}k\left(20-k\right)=20\times\frac{20\times21}{2}-\frac{20\times21\times41}{6}\end{array} \)
\(\begin{array}{l} =\frac{20\times21}{2}\left[20-\frac{41}{3}\right]=1330\end{array} \)
7. If the function \(\begin{array}{l} f\left(x\right)=\left\{\frac{\text{log}_e\left(1-x+x^2\right)+\text{log}_e\left(1+x+x^2\right)}{\underset{k,}{\sec x}-\cos x} \right.,\underset{x=0}{x\in\left(\frac{-\pi}{2},\frac{\pi}{2}\right)}-\left\{0 \right\}\end{array} \)
is continuous at x = 0, then k is equal to
(A) 1
(B) –1
(C) e
(D) 0
Answer (A)
Sol.
\(\begin{array}{l} f\left(x\right)=\left\{\frac{\text{log}_e\left(1-x+x^2\right)+\text{log}_e\left(1+x+x^2\right)}{\underset{k,}{\sec x}-\cos x} \right.,\underset{x=0}{x\in\left(\frac{-\pi}{2},\frac{\pi}{2}\right)}-\left\{0 \right\}\end{array} \)
for continuity at x = 0
\(\begin{array}{l} \displaystyle \lim_{x \to 0}f\left(x\right)=k\end{array} \)
\(\begin{array}{l} \therefore\ k=\displaystyle \lim_{x \to 0} \frac{\text{log}_e\left(x^4+x^2+1\right)}{\sec x-\cos x}\left(\frac{0}{0}\text{ form}\right)\end{array} \)
\(\begin{array}{l} =\displaystyle \lim_{x \to 0}\frac{\cos x\text{log}_e\left(x^4+x^2+1\right)}{\sin^2x}\end{array} \)
\(\begin{array}{l} =\displaystyle \lim_{x \to 0}\frac{\text{log}_e\left(x^4+x^2+1\right)}{x^2}\end{array} \)
\(\begin{array}{l} =\displaystyle \lim_{x \to 0}\frac{\text{In}\left(1+x^2+x^4\right)}{x^2+x^4}\cdot\frac{x^2+x^4}{x^2}= 1 \end{array} \)
8. If
\(\begin{array}{l} f\left(x\right)=\left\{\begin{matrix}x+a, & x\leq 0 \\\left|x-4\right|, & x>0 \\\end{matrix}\right.\text{ and }g\left(x\right)=\left\{\begin{matrix}x+1, & x<0 \\\left(x-4\right)^2+b, & x\geq 0 \\\end{matrix}\right.\end{array} \)
are continuous on R, then (gof) (2) + (fog) (–2) is equal to
(A) –10
(B) 10
(C) 8
(D) –8
Answer (D)
Sol.
\(\begin{array}{l} f\left(x\right)=\left\{\begin{matrix}x+a, & x\leq 0 \\\left|x-4\right|, & x>0 \\\end{matrix}\right.\text{ and }g\left(x\right)=\left\{\begin{matrix}x+1, & x<0 \\\left(x-4\right)^2+b, & x\geq 0 \\\end{matrix}\right.\end{array} \)
∵ f(x) and g(x) are continuous on R
∴ a = 4 and b = 1 – 16 = –15
then (gof)(2) + (fog) (–2)
= g(2) + f(–1)
= –11 + 3 = – 8
9. Let \(\begin{array}{l} f\left(x\right)=\left\{\begin{matrix}x^3-x^2+10x-7, & x\leq1 \\-2x+\text{log}_2\left(b^2-4\right), & x>1 \\\end{matrix}\right.\end{array} \)
Then the set of all values of b, for which f(x) has maximum value at x = 1, is
\(\begin{array}{l} \left(A\right) \left(-6, -2\right)\\ \left(B\right) \left(2, 6\right)\\ \left(C\right) \left[-6, -2) \cup (2, 6\right]\end{array} \)
\(\begin{array}{l} (\text{D})\ \left[-\sqrt{6},-2\right]\cup \left(2,\sqrt{6}\right] \end{array} \)
Answer (C)
Sol.
\(\begin{array}{l} f\left(x\right)=\left\{\begin{matrix}x^3-x^2+10x-7, & x\leq1 \\-2x+\text{log}_2\left(b^2-4\right), & x>1 \\\end{matrix}\right.\end{array} \)
If f(x) has maximum value at x = 1 then f(1+) ≤f(1)
–2 + log2(b2 – 4) ≤ 1 – 1 + 10 – 7
log2(b2 – 4) ≤ 5
0 <b2 – 4 ≤ 32
\(\begin{array}{l} \left(i\right) b^2 – 4 > 0 \Rightarrow b \in (-\infty, -2) \cup (2, \infty)\\ \left(ii\right) b^2 – 36 \le 0 \Rightarrow b\in \left[-6, 6\right]\end{array} \)
Intersection of above two sets
\(\begin{array}{l} b \in \left[-6, -2)\cup(2, 6\right]\end{array} \)
10. \(\begin{array}{l}If~ a=\displaystyle \lim_{n \to \infty}\sum_{k=1}^{n}\frac{2n}{n^2+k^2}\text{and}\end{array} \)
\(\begin{array}{l} f\left(x\right)=\sqrt{\frac{1-\cos x}{1+\cos x}},x\in\left(0,1\right),then\end{array} \)
\(\begin{array}{l} (\text{A})\ 2\sqrt{2}f\left(\frac{a}{2}\right)=f’\left(\frac{a}{2}\right)\end{array} \)
\(\begin{array}{l} (\text{B})\ f\left(\frac{a}{2}\right)f’\left(\frac{a}{2}\right)=\sqrt{2}\end{array} \)
\(\begin{array}{l} (\text{C})\ \sqrt{2}f\left(\frac{a}{2}\right)=f’\left(\frac{a}{2}\right)\end{array} \)
\(\begin{array}{l} (\text{D})\ f\left(\frac{a}{2}\right)=\sqrt{2}f’\left(\frac{a}{2}\right)\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l} a=\displaystyle \lim_{n \to \infty}\sum_{k=1}^{n}\frac{2n}{n^2+k^2}\end{array} \)
\(\begin{array}{l} =\displaystyle \lim_{n \to \infty}\frac{1}{n}\sum_{k=1}^{n}\frac{2}{1+\left(\frac{k}{n}\right)^2} \end{array} \)
\(\begin{array}{l} a=\displaystyle\int\limits_0^1\frac{2}{1+x^2}dx=2\tan^{-1}x\int_0^1=\frac{\pi}{2}\end{array} \)
\(\begin{array}{l} f\left(x\right)=\sqrt{\frac{1-\cos x}{1+\cos x}},x\in \left(0,1\right)\end{array} \)
\(\begin{array}{l} f\left(x\right)=\frac{1-\cos x}{\sin x}=\text{cosec } x-\cot x\end{array} \)
\(\begin{array}{l} f’\left(x\right)=\text{cosec}^2 x-\text{cosec } x\cot x \end{array} \)
\(\begin{array}{l} \left.\begin{matrix}f\left(\frac{a}{2}\right)=f\left(\frac{\pi}{4}\right)=\sqrt{2}-1 \\f’\left(\frac{a}{2}\right)=f’\left(\frac{\pi}{4}\right)=2-\sqrt{2}\end{matrix}\right\}f’\left(\frac{a}{2}\right)=\sqrt{2}.f\left(\frac{a}{2}\right)\end{array} \)
11. If \(\begin{array}{l} \frac{dy}{dx}+2y\tan x=\sin x,0<x<\frac{\pi}{2}\ \text{and}\ y\left(\frac{\pi}{3}\right)=0\end{array} \)
then the maximum value of y(x) is:
\(\begin{array}{l} (\text{A})\ \frac{1}{8}\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{3}{4}\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{1}{4}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{3}{8}\end{array} \)
Answer (A)
Sol.
\(\begin{array}{l} \frac{dy}{dx}+2y\tan x=\sin x\end{array} \)
which is a first order linear differential equation.
\(\begin{array}{l}\text{Integrating factor}(I. F.) =e^{\int 2\tan x\ dx} \end{array} \)
\(\begin{array}{l} =e^{2\text{In}|\sec x|}=\sec^2 x\end{array} \)
Solution of differential equation can be written as
\(\begin{array}{l} y\cdot\sec^2x=\int\sin x\cdot \sec^2 xdx=\int\sec x\cdot \tan xdx\end{array} \)
\(\begin{array}{l} y\sec^2 x=\sec x+C\end{array} \)
\(\begin{array}{l} y\left(\frac{\pi}{3}\right)=0,0=\sec\frac{\pi}{3}+C\Rightarrow C=-2\end{array} \)
\(\begin{array}{l}y=\frac{\sec x-2}{\sec^2 x}=\cos x-2\cos^2 x\end{array} \)
\(\begin{array}{l} =\frac{1}{8}-2\left(\cos x-\frac{1}{4}\right)^2 \end{array} \)
\(\begin{array}{l} y_{\text{max}}=\frac{1}{8}\end{array} \)
12. A point P moves so that the sum of squares of its distances from the points (1, 2) and (–2, 1) is 14. Let f(x, y) = 0 be the locus of P, which intersects the x-axis at the points A, B and the y-axis at the points C, D. Then the area of the quadrilateral ACBD is equal to
\(\begin{array}{l} (\text{A})\ \frac{9}{2} \end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{3\sqrt{17}}{2} \end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{3\sqrt{17}}{4} \end{array} \)
\(\begin{array}{l}(\text{C}) 9\end{array} \)
Answer (B)
Sol. Let point P : (h, k)
\(\begin{array}{l} \left(h – 1\right)^2 + \left(k – 2\right)^2 + \left(h + 2\right)^2 + \left(k – 1\right)^2 = 14\\ 2h^2 + 2k^2 + 2h – 6k – 4 = 0\end{array} \)
Locus of P : x2 + y2 + x – 3y – 2 = 0
Intersection with x-axis,
x2 + x – 2 = 0
⇒ x = –2, 1
Intersection with y-axis,
y2 – 3y – 2 = 0
\(\begin{array}{l} \Rightarrow y=\frac{3\pm\sqrt{17}}{2}\end{array} \)
\(\begin{array}{l}\text{Area of the quadrilateral ACBD is =}\frac{1}{2}\left(\left|x_1\right|+\left|x_2\right|\right)\left(\left|y_1\right|+\left|y_2\right|\right)\end{array} \)
\(\begin{array}{l} =\frac{1}{2}\times 3\times \sqrt{17}=\frac{3\sqrt{17}}{2}\end{array} \)
13. Let the tangent drawn to the parabola y2 = 24x at the point (α, β) is perpendicular to the line 2x + 2y = 5. Then the normal to the hyperbola \(\begin{array}{l} \frac{x^2}{\alpha^2}-\frac{y^2}{\beta^2}=1 \end{array} \)
at the point (α + 4, β + 4) does NOT pass through the point
(A) (25, 10)
(B) (20, 12)
(C) (30, 8)
(D) (15, 13)
Answer (D)
Sol. Any tangent to y2 = 24x at (α, β)
βy = 12(x + α)
\(\begin{array}{l}\text{Slope}=\frac{12}{\beta}\ \text{and perpendicular to}~ 2x + 2y = 5\end{array} \)
\(\begin{array}{l} \Rightarrow \frac{12}{\beta}=1\Rightarrow\ \beta=12,\alpha=6\end{array} \)
Hence, hyperbola is
\(\begin{array}{l} \frac{x^2}{36}-\frac{y^2}{144}=1\end{array} \)
and normal is drawn at (10, 16)
Equation of normal
\(\begin{array}{l} \frac{36\cdot x}{10}+\frac{144\cdot y}{16}=36+144 \end{array} \)
\(\begin{array}{l} \Rightarrow \frac{x}{50}+\frac{y}{20}=1 \end{array} \)
This does not pass though (15, 13) out of given option.
14. The length of the perpendicular from the point (1, –2, 5) on the line passing through (1, 2, 4) and parallel to the line x + y – z = 0 = x – 2y + 3z – 5 is
\(\begin{array}{l} (\text{A})\ \sqrt{\frac{21}{2}}\end{array} \)
\(\begin{array}{l} (\text{B})\ \sqrt{\frac{9}{2}}\end{array} \)
\(\begin{array}{l} (\text{C})\ \sqrt{\frac{73}{2}}\end{array} \)
\(\begin{array}{l}(\text{D}) 1 \end{array} \)
Answer (A)
Sol.
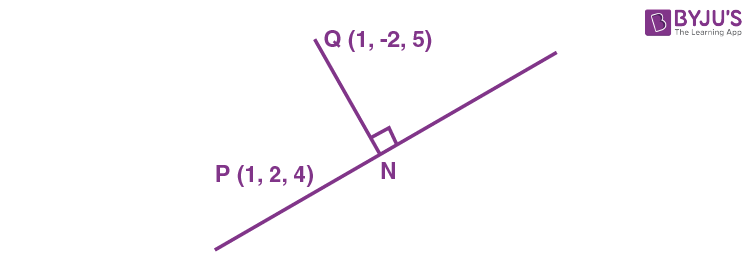
The line x + y – z = 0 = x – 2y + 3z – 5 is parallel to the vector
\(\begin{array}{l} \overrightarrow{b}=\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\1 & 1 & -1 \\1 & -2 & 3 \\\end{vmatrix}=\left(1,4,-3\right)\end{array} \)
Equation of line throughP(1, 2, 4) and parallel to
\(\begin{array}{l} \frac{x-1}{1}=\frac{y-2}{-4}=\frac{z-4}{-3}\end{array} \)
\(\begin{array}{l}Let N \equiv \left( \lambda + 1, -4\lambda + 2, -3\lambda + 4\right)\end{array} \)
\(\begin{array}{l} \overrightarrow{QN}= (\lambda, -4\lambda + 4, -3\lambda – 1)\end{array} \)
\(\begin{array}{l} \overrightarrow{QN}\ \text{is perpendicular to}\ \overrightarrow{b}\end{array} \)
\(\begin{array}{l} \Rightarrow (\lambda, -4\lambda + 4, -3\lambda – 1)\cdot(1, 4, -3) = 0\end{array} \)
\(\begin{array}{l} \Rightarrow\ \lambda=\frac{1}{2} \end{array} \)
\(\begin{array}{l} \text{Hence}~ \overrightarrow{QN}=\left(\frac{1}{2},2,\frac{-5}{2}\right) \end{array} \)
\(\begin{array}{l} \text{and}~\left| \overrightarrow{QN}\right|=\sqrt{\frac{21}{2}}\end{array} \)
15. Let \(\begin{array}{l} \vec{a}=\alpha\hat{i}+\hat{j}-\hat{k}\ \text{and}\ \vec{b}=2\hat{i}+\hat{j}-\alpha\hat{k},\alpha >0.\end{array} \)
\(\begin{array}{l}\text{If the projection of}\ \vec{a}\times \vec{b}\ \text{on the vector}\ -\hat{i}+2\hat{j}-2\hat{k}\end{array} \)
is 30, then α is equal to
\(\begin{array}{l} (\text{A})\ \frac{15}{2} \end{array} \)
\(\begin{array}{l} (\text{B}) 8\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{13}{2} \end{array} \)
\(\begin{array}{l} (\text{D}) 7\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l}Given \colon \vec{a}=\left(\alpha,1,-1\right)\end{array} \)
and \(\begin{array}{l} \vec{b}=\left(2,1,-\alpha\right)\end{array} \)
\(\begin{array}{l} \vec{c}=\vec{a}\times\vec{b}=\begin{vmatrix}\hat{i} & \hat{j} &\hat{k} \\\alpha & 1 & -1 \\2 & 1 & -\alpha \\\end{vmatrix}\end{array} \)
\(\begin{array}{l} =\left(-\alpha +1\right)\hat{i}+\left(\alpha^2-2\right)\hat{j}+\left(\alpha-2\right)\hat{k} \end{array} \)
\(\begin{array}{l}\text{Projection of }\vec{c}\ \text{on}\ \vec{d}=-\hat{i}+2\hat{j}-2\hat{k}\end{array} \)
\(\begin{array}{l} =\left|\vec{c}\cdot\frac{\vec{d}}{\left|d\right|}\right|=30\left\{\text{Given} \right\}\end{array} \)
\(\begin{array}{l} \Rightarrow\ =\left|\frac{\alpha-1-4+2\alpha^2-2\alpha+4}{\sqrt{1+4+4}}\right|=30\end{array} \)
On solving
\(\begin{array}{l} \alpha=\frac{-13}{2}\end{array} \)
(Rejected as α> 0)
and α = 7
16. The mean and variance of a binomial distribution are α and α/3, respectively. If P(X = 1) = 4/243 then P(X = 4 or 5) is equal to :
\(\begin{array}{l} (\text{A})\ \frac{5}{9} \end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{64}{81} \end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{16}{27} \end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{145}{243} \end{array} \)
Answer (C)
Sol. Given, mean = np = α.
and variance
\(\begin{array}{l} =npq=\frac{\alpha}{3}\end{array} \)
\(\begin{array}{l} \Rightarrow q=\frac{1}{3}\text{ and }p=\frac{2}{3}\end{array} \)
\(\begin{array}{l} P\left(X=1\right)=n.p^1.q^{n-1}=\frac{4}{243}\end{array} \)
\(\begin{array}{l}\Rightarrow n.\frac{2}{3}.\left(\frac{1}{3}\right)^{n-1}=\frac{4}{243}\Rightarrow n = 6\end{array} \)
\(\begin{array}{l} P\left(X=4 \text{ or } 5\right)=^6C_4.\left(\frac{2}{3}\right)^4\cdot\left(\frac{1}{3}\right)^2+^6C_5.\left(\frac{2}{5}\right)^5.\frac{1}{3}\end{array} \)
\(\begin{array}{l} =\frac{16}{27} \end{array} \)
17. Let E1, E2, E3 be three mutually exclusive events such that \(\begin{array}{l} P\left(E_1\right)=\frac{2+3p}{6},P\left(E_2\right)=\frac{2-p}{8}\ \text{and}\ P\left(E_3\right)=\frac{1-p}{2}.\end{array} \)
If the maximum and minimum values of p are p1 and p2, then (p1 + p2) is equal to :
\(\begin{array}{l} (\text{A})\ \frac{2}{3}\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{5}{3}\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{5}{4}\end{array} \)
\(\begin{array}{l} (\text{C})1\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l} 0\leq\frac{2+3P}{6}\leq 1\Rightarrow P\in \left[-\frac{2}{3},\frac{4}{3}\right]\end{array} \)
\(\begin{array}{l} 0\leq \frac{2-P}{8}\leq 1 \Rightarrow P\in \left[-6,2\right] \end{array} \)
\(\begin{array}{l} 0\leq \frac{1-P}{2}\leq 1 \Rightarrow P\in \left[-1,1\right] \end{array} \)
\(\begin{array}{l}0<P\left(E_1\right)+P\left(E_2\right)+P\left(E_3\right)\le1\end{array} \)
\(\begin{array}{l} 0<\frac{13}{12}-\frac{P}{8}\leq 1 \end{array} \)
\(\begin{array}{l} P\in \left[\frac{2}{3},\frac{26}{3}\right]\end{array} \)
Taking intersection of all
\(\begin{array}{l} P\in \left[\frac{2}{3},1\right)\end{array} \)
\(\begin{array}{l} P_1+P_2=\frac{5}{3}\end{array} \)
18. \(\begin{array}{l}\text{Let } S=\left\{\theta\in\left[0,2\pi\right]:8^{2\sin^2\theta}+8^{2\cos^2\theta} =16\right\} \end{array} \)
. \(\begin{array}{l}\text{Then}~ n\left(S\right)+\underset{\theta\in S}{\sum}\left(\sec\left(\frac{\pi}{4}+2\theta\right)\text{cosec}\left(\frac{\pi}{4}+2\theta\right)\right)\text{is equal to }:\end{array} \)
(A) 0
(B) – 2
(C) – 4
(D) 12
Answer (C)
Sol.
\(\begin{array}{l} S=\left\{\theta\in\left[0, 2\pi\right]:8^{2\sin^2\theta}+8^{2\cos^2\theta}=16 \right\}\end{array} \)
\(\begin{array}{l}\text{Now apply AM} \ge\text{ GM for }8^{2\sin^2\theta},8^{2\cos^2\theta}\end{array} \)
\(\begin{array}{l} \frac{8^{2\sin^2\theta}+8^{2\cos^2\theta}}{2}\ge\left(8^{2\sin^2\theta+2\cos^2\theta}\right)^\frac{1}{2} \end{array} \)
\(\begin{array}{l}8 \geq 8\end{array} \)
\(\begin{array}{l} \Rightarrow 8^{2\sin^2\theta}=8^{2\cos^2\theta}\end{array} \)
\(\begin{array}{l}\text{or}~sin^2\theta = cos^2\theta\end{array} \)
\(\begin{array}{l} \therefore \theta=\frac{\pi}{4},\frac{3\pi}{4},\frac{5\pi}{4},\frac{7\pi}{4}\end{array} \)
\(\begin{array}{l} n\left(S\right)+\underset{\theta\in S}{\sum}\sec\left(\frac{\pi}{4}+2\theta\right)\text{cosec}\left(\frac{\pi}{4}+2\theta\right)\end{array} \)
\(\begin{array}{l} 4+\underset{\theta\in S}{\sum}\frac{2}{2\sin\left(\frac{\pi}{4}+2\theta\right)\cos\left(\frac{\pi}{4}+2\theta\right)} \end{array} \)
\(\begin{array}{l} =4+\underset{\theta\in S}{\sum}\frac{2}{\sin\left(\frac{\pi}{2}+4\theta\right)}=4+2\underset{\theta\in S}{\sum}\text{cosec}\left(\frac{\pi}{2}+4\theta\right)\end{array} \)
\(\begin{array}{l} =4+2\left[\text{cosec}\left(\frac{\pi}{2}+\pi\right)+\text{cosec}\left(\frac{\pi}{2}+3\pi\right)+.\text{cosec}\left(\frac{\pi}{2}+5\pi\right)+\text{cosec}\left(\frac{\pi}{2}+7\pi\right)\right]\end{array} \)
\(\begin{array}{l} =4+2\left[-\text{cosec}\frac{\pi}{2}-\text{cosec}\frac{\pi}{2}-\text{cosec}\frac{\pi}{2}-\text{cosec}\frac{\pi}{2}\right]\end{array} \)
\(\begin{array}{l} =4+2\left[-\text{cosec}\frac{\pi}{2}-\text{cosec}\frac{\pi}{2}-\text{cosec}\frac{\pi}{2}-\text{cosec}\frac{\pi}{2}\right] \end{array} \)
= 4– 2(4)
= 4 – 8
= – 4
19. \(\begin{array}{l} \tan\left(2\tan^{-1}\frac{1}{5}+\sec^{-1}\frac{\sqrt{5}}{2}+2\tan^{-1}\frac{1}{8}\right)\end{array} \)
is equal to :
\(\begin{array}{l} (\text{A}) 1\end{array} \)
\(\begin{array}{l} (\text{B}) 2\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{1}{4} \end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{5}{4} \end{array} \)
Answer (B)
Sol.
\(\begin{array}{l} \tan\left(2\tan^{-1}\frac{1}{5}+\sec^{-1}\frac{\sqrt{5}}{2}+2\tan^{-1}\frac{1}{8}\right) \end{array} \)
\(\begin{array}{l} =\tan\left(2\tan^{-1}\left(\frac{\frac{1}{5}+\frac{1}{8}}{1-\frac{1}{5}.\frac{1}{8}}\right)+\sec^{-1}\frac{\sqrt{5}}{2}\right)\end{array} \)
\(\begin{array}{l} =\tan\left[2\tan^{-1}\frac{1}{3}+\tan^{-1}\frac{1}{2}\right]\end{array} \)
\(\begin{array}{l} =\tan\left[\tan^{-1}\frac{\frac{2}{3}}{1-\frac{1}{9}}+\tan^{-1}\frac{1}{2}\right] \end{array} \)
\(\begin{array}{l} =\tan\left[\tan^{-1}\frac{3}{4}+\tan^{-1}\frac{1}{2}\right]\end{array} \)
\(\begin{array}{l} =\tan\left[\tan^{-1}\frac{\frac{3}{4}+\frac{1}{2}}{1-\frac{3}{8}}\right]=\tan\left[\tan^{-1}\frac{\frac{5}{4}}{\frac{5}{8}}\right]\end{array} \)
\(\begin{array}{l} =\tan\left[\tan^{-1}2\right]=2\end{array} \)
20. The statement \(\begin{array}{l} \left(\sim\left(p\ \Leftrightarrow \sim q\right)\right)\wedge q\end{array} \)
is :
(A) A tautology
(B) A contradiction
\(\begin{array}{l}\left(C\right)\text{Equivalent to} \left ( p \Rightarrow q \right) \wedge q\end{array} \)
\(\begin{array}{l}\left(D\right)\text{Equivalent to} \left ( p \Rightarrow q \right) \wedge p\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l}\sim \left(p\Leftrightarrow ~ \sim q\right) \wedge q\\ = \left(p\Leftrightarrow q\right) \wedge q\end{array} \)
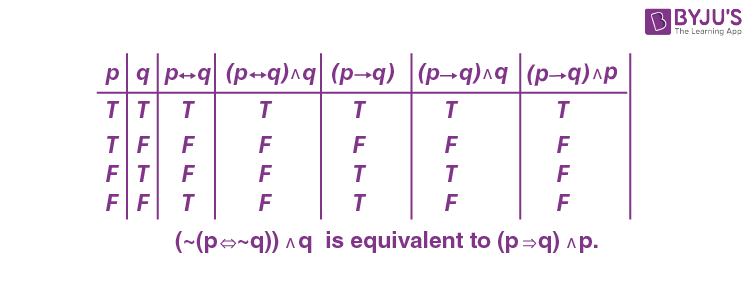
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, –00.33, –00.30, 30.27, –27.30) using the mouse and the on-screen virtual numeric keypad in the place designated to enter the answer.
1. If for some p, q, r ∈ R, not all have same sign, one of the roots of the equation (p2 + q2)x2 – 2q(p + r)x + q2 + r2 = 0 is also a root of the equation x2 + 2x – 8 = 0, then (q2 + r2)/p2 is equal to __________.
Answer (272)
Sol. Let α and β be the roots of (p2 + q2) x2 – 2q(p + r)x + q2 + r2 = 0
∴ α + β> 0 and αβ> 0
Also, it has a common root with x2 + 2x – 8 = 0
∴ The common root between above two equations is 4.
⇒ 16(p2 + q2) – 8q(p + r) + q2 + r2 = 0
⇒ (16p2 – 8pq + q2) + (16q2 – 8qr + r2) = 0
⇒ (4p – q)2 + (4q – r)2 = 0
⇒ q = 4p and r = 16p
\(\begin{array}{l} \therefore \frac{q^2+r^2}{p^2}=\frac{16p^2+256p^2}{p^2}=272\end{array} \)
2. The number of 5-digit natural numbers, such that the product of their digits is 36, is _________.
Answer (180)
Sol. Factors of 36 = 22⋅ 32⋅ 1
Five-digit combinations can be
(1, 2, 2, 3, 3) (1, 4, 3, 3, 1), (1, 9, 2, 2, 1)
(1, 4, 9, 11) (1, 2, 3, 6, 1) (1, 6, 6, 1, 1)
i.e., total numbers
\(\begin{array}{l} \frac{5!}{2!2!}+\frac{5!}{2!2!}+\frac{5!}{2!2!}+\frac{5!}{3!}+\frac{5!}{2!}+\frac{5!}{3!2!}\end{array} \)
= (30 × 3) + 20 + 60 + 10 = 180.
3. The series of positive multiples of 3 is divided into sets: {3}, {6, 9, 12}, {15, 18, 21, 24, 27},…… Then the sum of the elements in the 11th set is equal to ________.
Answer (6993)
Sol. Given series
∴ 11th set will have 1 + (10)2 = 21 term
Alsoupto 10th set total 3 × k type terms will be
1 + 3 + 5 +……+19 = 100 – term
∴ Set 11 = {3 × 101, 3 × 102,……3 × 121}
∴ Sum of elements = 3 × (101 + 102 +…+121)
\(\begin{array}{l} =\frac{3\times222\times21}{2}=6993 \end{array} \)
4. The number of distinct real roots of the equation x5(x3 – x2 – x + 1) + x (3x3 – 4x2 – 2x + 4) – 1 = 0 is __________.
Answer (3)
Sol. x8 – x7 – x6 + x5 + 3x4 – 4x3 – 2x2 + 4x – 1 = 0
⇒ x7(x – 1) – x5(x – 1) + 3x3(x – 1) – x (x2 – 1) + 2x (1 – x) + (x – 1) = 0
⇒ (x – 1) (x7 – x5 + 3x3 – x(x + 1) – 2x + 1) = 0
⇒ (x – 1) (x7 – x5 + 3x3 –x2 – 3x + 1) = 0
⇒ (x – 1) (x5 (x2 – 1) + 3x (x2 – 1) – 1 (x2 – 1)) = 0
⇒ (x – 1) (x2 – 1) (x5 + 3x – 1) = 0
∴ x = ± 1 are roots of above equation and x5 + 3x – 1 is a monotonic term hence vanishs at exactly one value of x other then 1 or – 1.
∴ 3 real roots.
5. If the coefficients of x and x2 – in the expansion of (1 + x)p (1 – x)q, p, q≤ 15, are – 3 and – 5 respectively, then coefficient of x3 is equal to ______.
Answer (23)
Sol. Coefficient of x in (1 + x)p (1 – x)q
\(\begin{array}{l} -^p{C_0}\ ^qC_1 +\ ^p{C_1}\ ^q{C_0}=-3\Rightarrow p-q=-3 \end{array} \)
Coefficient of x2 in (1 + x)p (1 – x)q
\(\begin{array}{l} ^pC_0\ ^qC_2 -\ ^pC_1\ ^qC_1\ +\ ^pC_2 \ ^qC_0 =-5\end{array} \)
\(\begin{array}{l} \frac{q\left(q-1\right)}{2}-pq+\frac{p\left(p-1\right)}{2}=-5\end{array} \)
\(\begin{array}{l} \frac{q^2-q}{2}-\left(q-3\right)q+\frac{\left(q-3\right)\left(q-4\right)}{2}=-5 \end{array} \)
⇒ q = 11, p = 8
Coefficient of x3 in (1 + x)8 (1 – x)11 is
\(\begin{array}{l} =-^{11}C_3 +\ ^8C_1\ ^{11}C_2-\ ^8C_2\ ^{11}C_1 +\ ^8C_3=23\end{array} \)
6. If \(\begin{array}{l} n\left(2n+1\right)\int_0^1\left(1-x^n\right)^{2n}dx=1177\int_0^1\left(1-x^n\right)^{2n+1}dx\end{array} \)
, then n ∈ N is equal to ______.
Answer (24)
Sol.
\(\begin{array}{l} \int_0^1\left(1-x^n\right)^{2n+1}dx=\int_0^1 1.\left(1-x^n\right)^{2n+1}dx\end{array} \)
\(\begin{array}{l} =\left[\left(1-x^n\right)^{2n+1}\cdot x\right]_0^1-\int_0^1x\cdot\left(2n+1\right) \left(1-x^n\right)^{2n}\cdot-nx^{n-1}dx\end{array} \)
\(\begin{array}{l} =n\left(2n+1\right)\int_0^1\left(1-\left(1-x^n\right)\right)\left(1-x^n\right)^{2n}dx\end{array} \)
\(\begin{array}{l} =n\left(2n+1\right)\int_0^1\left(1-x^n\right)^{2n}dx-n\left(2n+1\right)\int_0^1\left(1-x^n\right)^{2n+1}dx\end{array} \)
\(\begin{array}{l} \left(1+n\left(2n+1\right)\right)\int_0^1\left(1-x^n\right)^{2n+1}dx=n\left(2n+1\right)\int_0^1\left(1-x^n\right)^{2n}dx\end{array} \)
\(\begin{array}{l} \left(2n^2+n+1\right)\int_0^1\left(1-x^n\right)^{2n+1}dx=1177\int_0^1\left(1-x^n\right)^{2n+1}dx \end{array} \)
∴ 2n2 + n + 1 = 1177
2n2 + n – 1176 = 0
\(\begin{array}{l}\therefore n=24 \text{ or }-\frac{49}{2}\end{array} \)
∴ n = 24
7. Let a curve y = y(x) pass through the point (3, 3) and the area of the region under this curve, above the x-axis and between the abscissae 3 and \(\begin{array}{l} x\left(>3\right)be\left(\frac{y}{x}\right)^3\end{array} \)
. If this curve also passes through the point \(\begin{array}{l} \left(\alpha, 6\sqrt{10}\right)\end{array} \)
in the first quadrant, then α is equal to _______.
Answer (6)
Sol.
\(\begin{array}{l} \displaystyle\int\limits_3^xf\left(x\right)dx=\left(\frac{f\left(x\right)}{x}\right)^3\end{array} \)
\(\begin{array}{l} x^3\cdot\displaystyle\int\limits_3^xf\left(x\right)dx=f^3\left(x\right)\end{array} \)
Differentiate w.r.t. x
\(\begin{array}{l} x^3f\left(x\right) +3x^2\cdot\frac{f^3\left(x\right)}{x^3}=3f^2\left(x\right)f’\left(x\right)\end{array} \)
\(\begin{array}{l} \Rightarrow 3y^2\frac{dy}{dx}=x^3y+\frac{3y^3}{x}\end{array} \)
\(\begin{array}{l} 3xy\frac{dy}{dx}=x^4+3y^2\end{array} \)
Let y2 = t
\(\begin{array}{l} \frac{3}{2}\frac{dt}{dx}=x^3+\frac{3t}{x} \end{array} \)
\(\begin{array}{l} \frac{dt}{dx}-\frac{2t}{x}=\frac{2x^3}{3}\end{array} \)
\(\begin{array}{l} I.F.=\cdot e^{\int-\frac{2}{x}dx}=\frac{1}{x^2} \end{array} \)
Solution of differential equation
\(\begin{array}{l} t\cdot\frac{1}{x^2}=\int\frac{2}{3}x\ dx \end{array} \)
\(\begin{array}{l} \frac{y^2}{x^2}=\frac{x^2}{3}+C \end{array} \)
\(\begin{array}{l} y^2=\frac{x^4}{3}+Cx^2\end{array} \)
\(\begin{array}{l}\text{Curve passes through} (3, 3) \Rightarrow C = – 2\\y^2=\frac{x^4}{3}-2x^2\end{array} \)
\(\begin{array}{l}\text{Which passes through }\left(\alpha,6\sqrt{10}\right) \end{array} \)
\(\begin{array}{l} \frac{\alpha^4-6\alpha^2}{3}=360 \end{array} \)
\(\begin{array}{l} \alpha^4-6\alpha^2-1080=0\\ \alpha = 6\end{array} \)
8. The equations of the sides AB, BC and CA of a triangle ABC are 2x + y = 0, x + py = 15a and x – y = 3, respectively. If its orthocentre is \(\begin{array}{l} \left(2,a\right),-\frac{1}{2}<a<2\end{array} \)
then p is equal to _______.
Answer (3)
Sol.
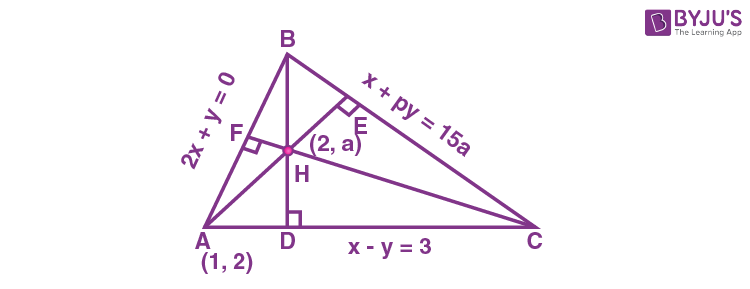
\(\begin{array}{l}\text{Slope of AH}=\frac{a+2}{1}\end{array} \)
\(\begin{array}{l}\text{Slope of BC}=-\frac{1}{p} \end{array} \)
∴ p = a + 2 …(i)
\(\begin{array}{l}\text{Coordinate of } C=\left(\frac{18p-30}{p+1},\frac{15p-33}{p+1}\right)\end{array} \)
\(\begin{array}{l}\text{Slope of HC} =\frac{\frac{15p-33}{p+1}-a}{\frac{18p-30}{p+1}-2}=\frac{15p-33-\left(p-2\right)\left(p+1\right)}{18p-30-2p-2}\end{array} \)
\(\begin{array}{l} =\frac{16p-p^2-31}{16p-32}\end{array} \)
\(\begin{array}{l} \because\ \frac{16p-p^2-31}{16p-32}\times -2=-1 \end{array} \)
∴ p2 – 8p + 15 = 0
∴ p = 3 or 5
But if p = 5 then a = 3 not acceptable
∴ p = 3
9. Let the function f(x) = 2x2 – logex, x> 0, be decreasing in (0, a) and increasing in (a, 4). A tangent to the parabola y2 = 4ax at a point P on it passes through the point (8a, 8a –1) but does not pass through the point (-1/a, 0). If the equation of the normal at P is \(\begin{array}{l} \frac{x}{\alpha}+\frac{y}{\beta}=1 \end{array} \)
then α + β is equal to ________.
Answer (45)
Sol.
\(\begin{array}{l} \delta’\left(x\right)=\frac{4x^2-1}{x} \end{array} \)
so f(x) is decreasing in \(\begin{array}{l} \left(0,\frac{1}{2}\right)\end{array} \)
and increasing in \(\begin{array}{l} \left(\frac{1}{2},\infty\right)\Rightarrow a=\frac{1}{2}\end{array} \)
\(\begin{array}{l}\text {Tangent at}~ y^2 = 2x \Rightarrow y = mx+\frac{1}{2m}\end{array} \)
It is passing through (4, 3)
\(\begin{array}{l} 3=4m+\frac{1}{2m}\Rightarrow m=\frac{1}{2}\text{ or }\frac{1}{4}\end{array} \)
So tangent may be
\(\begin{array}{l} y=\frac{1}{2}x+1\text{ or }y=\frac{1}{4}x+2 \end{array} \)
But
\(\begin{array}{l} y=\frac{1}{2}x+1\end{array} \)
passes through (–2, 0) so rejected.
Equation of Normal
\(\begin{array}{l} y=-4x-2\left(\frac{1}{2}\right)\left(-4\right)-\frac{1}{2}\left(-4\right)^3\end{array} \)
or
\(\begin{array}{l} y=-4x+4+32 \end{array} \)
or
\(\begin{array}{l} \frac{x}{9}+\frac{y}{36}=1\end{array} \)
10. Let Q and R be two points on the line \(\begin{array}{l} \frac{x+1}{2}=\frac{y+2}{3}=\frac{z-1}{2}\ \text{at a distance}\ \sqrt{26}\end{array} \)
from the point P(4, 2, 7). Then the square of the area of the triangle PQR is ________.
Answer (153)
Sol.
\(\begin{array}{l} L:\frac{x+1}{2}=\frac{y+2}{3}=\frac{z-1}{2}\end{array} \)
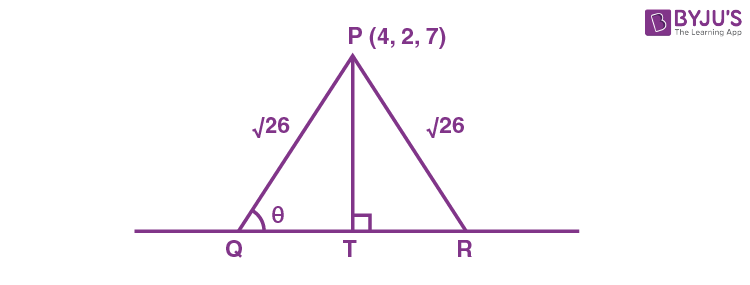
Let T(2t – 1, 3t – 2, 2t + 1)
\(\begin{array}{l} \because\ PT\perp^r QR \end{array} \)
∴ 2(2t – 5) + 3 (3t – 4) + 2 (2t – 6) = 0
17t = 34 ∴ t = 2 So T(3, 4, 5)
\(\begin{array}{l} \therefore\ PT=\sqrt{1+4+4}=3\end{array} \)
\(\begin{array}{l} \therefore\ QT=\sqrt{26-9}=\sqrt{17} \end{array} \)
\(\begin{array}{l}\therefore \text{Area of} ~\triangle PQR =\frac{1}{2}\times 2\sqrt{17}\times 3=3\sqrt{17}\end{array} \)
\(\begin{array}{l} \therefore\text {Square of ar}(\triangle PQR) = 153.\end{array} \)
JEE Main 2022 July 26th Shift 1 Paper Analysis


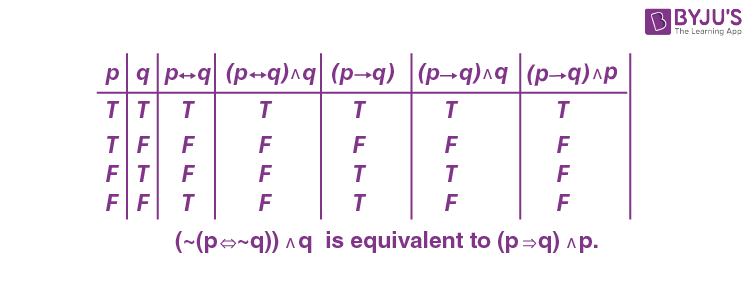













Comments