JEE Main Maths Syllabus 2024 - Download Latest Syllabus PDF

The JEE Main 2024 Mathematics syllabus is released by the National Testing Agency. On this page, you can check the complete JEE Main 2024 syllabus for Mathematics that is published by NTA. Students are advised to download the PDF of the JEE Main 2024 Mathematics syllabus for reference.

The National Testing Agency (NTA) is in charge of overlooking the JEE Main examination and all the related things, such as releasing admit cards, announcing the results, and more. The syllabus mostly remains unchanged despite other changes, especially in the exam pattern. In any case, students can go through the JEE Main Maths syllabus, which will help them formulate a proper strategy for studying in an organised manner for IIT JEE 2024.

JEE Main Maths Syllabus

Each and every concept included in JEE Main syllabus for Maths is important, and the questions could be expected from anywhere. Understanding JEE Main maths syllabus will help the engineering aspirants to develop a clear understanding of what concepts are to be prepared or avoided for better results in JEE Main. For Mathematics, the most important thing that students need to have is rigorous practice. The more problems students practise, the better they will be at solving questions with accuracy and speed. Apart from this, the students can also check the detailed subject-wise list of all the topics included in JEE Main Physics and Chemistry syllabi from below-given links.

Download JEE Main Syllabus

Students can download the PDF of the whole JEE Main 2024 syllabus for Maths below.

Download JEE Main Maths Syllabus PDF

JEE candidates can also view the detailed list of all the concepts mentioned below.

JEE Main Maths Syllabus Topics

Unit 1: Sets, Relations, and Functions

Sets and their representation.
Union, intersection, and complement of sets and their algebraic properties.
Powerset.
Relation, types of relations, equivalence relations.
Functions; one-one, into and onto functions, the composition of functions.

Unit 2: Complex Numbers and Quadratic Equations

Complex numbers as ordered pairs of reals.
Representation of complex numbers in the form (a+ib) and their representation in a plane, Argand diagram.
Algebra of complex numbers, modulus and argument (or amplitude) of a complex number, square root of a complex number.
Triangle inequality.
Quadratic equations in real and complex number system and their solutions.
The relation between roots and coefficients, nature of roots, the formation of quadratic equations with given roots.

Unit 3: Matrices and Determinants

Matrices: Algebra of matrices, types of matrices, and matrices of order two and three.
Determinants: Properties of determinants, evaluation of determinants, the area of triangles using determinants.
Adjoint and evaluation of inverse of a square matrix using determinants and elementary transformations.
Test of consistency and solution of simultaneous linear equations in two or three variables using determinants and matrices.

Unit 4: Permutations and Combinations

The fundamental principle of counting.
Permutation as an arrangement and combination as a selection.
The meaning of P (n,r) and C (n,r), simple applications.

Unit 5: Mathematical Induction

The principle of mathematical induction and its simple applications.

Unit 6: Binomial Theorem and its Simple Applications

Binomial theorem for a positive integral index.
General term and middle term.
Properties of Binomial coefficients and simple applications.

Unit 7: Sequence and Series

Arithmetic and geometric progressions, insertion of arithmetic, geometric means between two given numbers.
The relation between A.M. and G.M sum up to n terms of special series: Sn, Sn2, Sn3.
Arithmetico-Geometric progression.

Unit 8: Limit, Continuity and Differentiability

Real-valued functions, algebra of functions, polynomials, rational, trigonometric, logarithmic and exponential functions, inverse functions.
Graphs of simple functions.
Limits, continuity, and differentiability.
Differentiation of the sum, difference, product, and quotient of two functions.
Differentiation of trigonometric, inverse trigonometric, logarithmic, exponential, composite and implicit functions; derivatives of order up to two.
Rolle’s and Lagrange’s mean value theorems.
Applications of derivatives: Rate of change of quantities, monotonic increasing and decreasing functions, Maxima, and minima of functions of one variable, tangents, and normal.

Unit 9: Integral Calculus

Integral as an antiderivative.
Fundamental integrals involving algebraic, trigonometric, exponential and logarithmic functions.
Integration by substitution, by parts, and by partial fractions.
Integration using trigonometric identities.
Integral as limit of a sum.
Evaluation of simple integrals:

JEE Main Maths Syllabus 2019

Fundamental theorem of calculus.

Properties of definite integrals, evaluation of definite integrals, determining areas of the regions bounded by simple curves in standard form.

Unit 10: Differential Equations

Ordinary differential equations, their order, and degree.
Formation of differential equations.
The solution of differential equations by the method of separation of variables.
The solution of a homogeneous and linear differential equation of the type:

JEE Main Maths Syllabus 2019

Unit 11: Coordinate Geometry

Cartesian system of rectangular coordinates in a plane, distance formula, section formula, locus, and its equation, translation of axes, the slope of a line, parallel and perpendicular lines, intercepts of a line on the coordinate axes.
Straight lines: Various forms of equations of a line, intersection of lines, angles between two lines, conditions for concurrence of three lines.
Distance of a point from a line, equations of internal and external bisectors of angles between two lines, coordinates of the centroid, orthocentre, and circumcentre of a triangle, equation of the family of lines passing through the point of intersection of two lines.
Circles, conic sections: Standard form of the equation of a circle, the general form of the equation of a circle, its radius and centre, equation of a circle when the endpoints of a diameter are given, points of intersection of a line and a circle with the centre at the origin and condition for a line to be tangent to a circle, equation of the tangent.
Sections of conics, equations of conic sections (parabola, ellipse, and hyperbola) in standard forms, condition for y = mx + c to be a tangent and point (s) of tangency.

Unit 12: 3D Geometry

Coordinates of a point in space, the distance between two points.
Section formula, direction ratios and direction cosines, the angle between two intersecting lines.
Skew lines, the shortest distance between them and its equation.
Equations of a line and a plane in different forms, the intersection of a line and a plane, coplanar lines.

Unit 13: Vector Algebra

Vectors and scalars, the addition of vectors, components of a vector in two dimensions and three-dimensional space.
Scalar products and vector products, and vector triple product.

Unit 14: Statistics and Probability

Measures of Dispersion: Calculation of mean, median, mode of grouped and ungrouped data calculation of standard deviation, variance and mean deviation for grouped and ungrouped data.
Probability: Probability of an event, addition and multiplication theorems of probability, Baye’s theorem, probability distribution of a random variate, Bernoulli trials, and binomial distribution.

Unit 15: Trigonometry

Trigonometrical identities and equations.
Trigonometrical functions, inverse trigonometrical functions, and their properties.
Heights, and distance.

Unit 16: Mathematical Reasoning

Statements and logical operations: or, and, implies, implied by, if and only if, understanding of tautology, contradiction, converse, and contrapositive.

The JEE Main Maths syllabus mainly comprises all the topics included in Class XI and Class XII Maths syllabi. Students are advised to prepare a list of all the important Maths concepts in JEE Main syllabus and practise rigorously to ensure a meritorious position in the exam.

Also, read:

Sure Shot Topics for Mathematics – JEE Main

Tips to Revise Maths JEE Main Syllabus in 3 Months

100 Most Important Maths JEE Main Questions – Part 1

100 Most Important Maths JEE Main Questions – Part 2

5 Common Mistakes to Avoid in JEE Maths Exam

Frequently Asked Questions

Q1

Who publishes the JEE Main 2024 syllabus?

The National Testing Authority publishes the JEE Main 2024 syllabus.

Q2

Are there any changes in the JEE Main 2024 Mathematics syllabus?

The NTA has released the JEE Main 2024 Mathematics syllabus, and there are no changes in the syllabus.

Q3

When will the authorities release the JEE Main syllabus 2024?

The NTA released the syllabus and the official JEE Main 2024 notification.

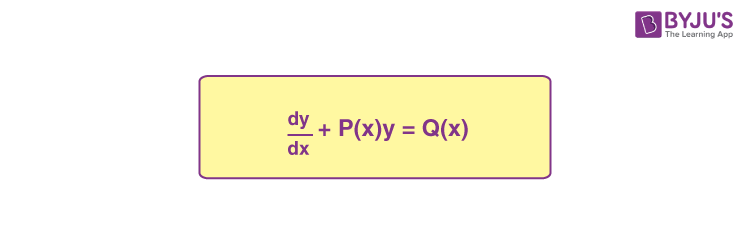
Comments

Leave a Comment Cancel reply