JEE Main 2020 Maths Paper With Solutions Shift 2 Sept 6

1. If the normal at an end of a latus rectum of an ellipse passes through an extremity of the minor axis, then the eccentricity e of the ellipse satisfies:

1) e⁴+2e²-1 = 0
2) e²+2e-1 = 0
3) e⁴+e²-1 = 0
4) e²+e-1 = 0

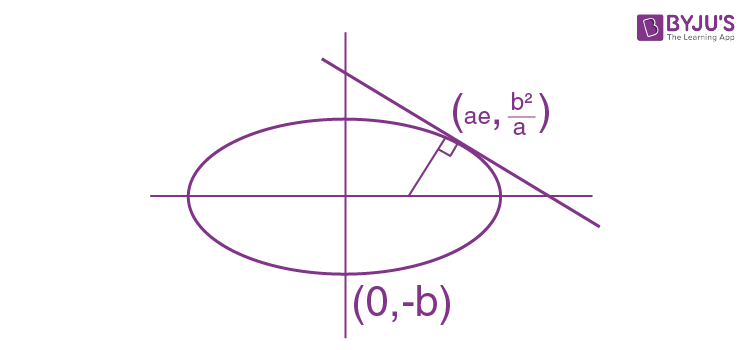
Equation of normal at (ae, b²/a)

(a²x/ae)-b²y/(b²/a) = a²e²

(ax/e)-ay = a²e²

⇒ (x/e)-y = ae²

It passes through (0,-b)

-b = ae² ⇒b² = a²e⁴

a² (1- e² ) = a²e⁴

⇒ e⁴+e²-1 = 0

Answer: (3)

2. The set of all real values of λ for which the function f(x) = (1-cos² x)(λ+sinx) , x∈(-π/2, π/2), has exactly one maxima and exactly one minima, is:

1) (-3/2, 3/2)-{0}
2) (-1/2, ½)-{0}
3) (-3/2, 3/2)
4) (-1/2, 1/2)

f(x) = (1-cos²x) (λ+sinx)

f(x) = sin²x (λ+sinx)

f’(x) = 2sinx cosx (λ +sinx) + sin²x (cosx)

= sin 2x(λ+sin x+ (sin x)/2)

= sin 2x(2λ+3sin x)

For extreme value f’(x) = 0

sin2x = 0 ⇒ sinx = 0

⇒ x = 0 → One point

2λ+3sinx = 0

⇒ sinx = -2λ/3

sinx ∈(-1,1)-{0}

-1<-2λ/3 <1

⇒ -3/2 <λ<3/2

λ∈(-3/2, 3/2)-{0}

Answer: (1)

3. The probabilities of three events A, B and C are given by P(A) = 0.6, P(B) = 0.4 and P(C) = 0.5. If P (A∪B) = 0.8, P (A∩C) = 0.3, P (A∩B∩C) = 0.2, P (B∩C) = β and P(A∪B ∪C) = α , where 0.85 ≤α≤ 0.95 , then β lies in the interval:

1) [0.36,0.40]
2) [0.25,0.35]
3) [0.35,0.36]
4) [0.20,0.25]

P(A∪B∪C) = P(A)+P(B)+P(C)-P(A∩B)-P(B∩C)-P(C∩A) + P(A∩B∩C)

α = 0.6+0.4+0.5-P(A∩B)-β-0.3+0.2

α = 1.4-P(A∩B)-β

⇒ α+β = 1.4-P(A∩B) ……..(i)

again

P(A∪B) = P(A)+P(B)-P(A∩B)

0.8 = 0.6+0.4-P(A∩B)

P(A∩B) = 0.2 ……..(ii)

Put the value P(A∩B) in equation (i)

α+β = 1.2

α = 1.2-β

0.85 ≤α≤ 0.95

⇒ 0.8 ≤1.2-β≤ 0.95

β∈ [0.25, 0.35]

Answer: (2)

4. The common difference of the A.P. b₁, b₂,….. b_m is 2 more than the common difference >of A.P. a₁, a₂, …a_n. If a₄₀ = -159, a₁₀₀ = -399 and b₁₀₀ = a₇₀, then b₁ is equal to:

1) -127
2) 81
3) 127
4) -81

A.P (a₁, a₂, a₃ ……….a_n) (CD = D_a)

(b₁, b₂, b₃ ………. b_m) (CD = D_b)

D_b = D_a+2

a₄₀ = -159

a₁+39D_a = -159 …(i)

a₁₀₀ = -399

a₁+99D_a = -399 …(ii)

Eqn (i)-(ii)

-60D_a = 240

⇒ D_a = -4

D_b = -4+2 = -2

a₁+39(-4) = -159

⇒ a₁ = -3

b₁₀₀ = a₇₀

b₁+99D_b = a₁+69D_a

b₁+99 (-2) = (-3)+69(-4)

b₁ = -81

Answer: (4)

5. The integral

1) e(4e-1)
2) e(4e+1)
3) 4e²-1
4) e(2e-1)

Put e^x.x^x = t

Since upper limit = e².2², Lower Limit = e

(e^x.x^x + e^x x^x(1+lnx)) dx = dt

e^x.x^x(2+lnx) dx = dt

= 4e²-e

= e(4e-1)

Answer: (1)

6. If the tangent to the curve, y = f(x) = xlog_ex, (x>0) at a point (c,f(c)) is parallel to the line-segment joining the points (1,0) and (e,e), then c is equal to:

1) e^(1/1-e)
2) (e-1)/e
3) 1/(e-1)
4) e^(1/e-1)

y = f(x) = x lnx

slope of the line joining (1, 0), (e, e)

m₂ = (e/e-1)

m₂ = m₁ ⇒ ln c+1 = e/(e-1)

ln c = (e/e-1)-1

= 1/(e-1)

c = e^(1/e-1)

Answer: (4)

7. If y = ((2/π)x-1) cosec x is the solution of the differential equation, (dy/dx)+p(x)y = ((2/π)-1)cosec x, 0<x,π/2, then the function p(x) is equal to:

1) cosec x
2) cot x
3) tan x
4) sec x

y = ((2/π)x-1)cosec x

Differentiate w.r.t.x

(dy/dx) = (2/π)cosec x-((2x/π)-1)cosec x.cot x

(dy/dx) +(2x/π-1)cosec x.cot x = (2/π) cosec x

(dy/dx)+y cot x = (2/π) cosec x

Compare this differential equation with given differential equation

p(x) = cot x

Answer: (2)

8. If α and β are the roots of the equation 2x(2x+1) = 1, then β is equal to:

1) 2α(α-1)
2) -2α(α+1)
3) 2α²
4) 2α(α+1)

2x(2x+1) = 1

If α and β are the roots i.e α and β satisfy this equation

2α(2α+1) = 1

⇒ α(2α+1) = ½

4x²+2x-1 = 0

α + β = -1/2

= -α(2α+1)

β = -α(2α+1)-α

= -α(2α+2)

= -2α(α+1)

Answer: (2)

9. For all twice differentiable functions f: R→ R, with f(0) = f(1) = f’(0) = 0,

1) f”(x) = 0, at every point x∈(0,1)
2) f”(x) ≠ 0, at every point x∈(0,1)
3) f”(x) = 0, for some x∈(0,1)
4) f”(0) = 0

Applying rolle’s theorem in [0,1] for function f(x)

f’(c) = 0, c ∈(0,1)

again applying rolles theorem in [0,c] for function f'(x) s

f’’(c₁) = 0, c₁∈(0,c)

Answer: (3)

10. The area (in sq.units) of the region enclosed by the curves y = x²-1 and y = 1-x² is equal to:

1) 4/3
2) 7/2
3) 16/3
4) 8/3

Total area =

= 4(1-1/3)

= 8/3 sq. unit

Answer: (4)

11. For a suitably chosen real constant a, let a function, f:R-{-a}→R be defined by f(x) = (a-x)/(a+x). further suppose that for any real number x ≠ -a and f(x) ≠ -a, (fof)(x) = x. Then f(-1/2) is equal to:

1) -3
2) 3
3) 1/3
4) -1/3

f(x) = (a-x)/(a+x)

f(f(x)) = (a-f(x))/(a+f(x)) = x

(a-ax)/(1+x) = f(x) = (a-x)/(a+x)

a(1-x)/(1+x) = (a-x)/(a+x)

⇒ a = 1

So f(x) = (1-x)/(1+x)

f(-1/2) = 3

Answer: (2)

12. Let θ = π/5 and A =

1) is one
2) lies in (1,2)
3) lies in (2,3)
4) is zero

B = A+A⁴

A² =

=

Similarly

A⁴ =

B = A⁴+A

=

=

det B = (cos4θ+cos θ)² +(sin 4θ+sin θ)²

= cos²4θ + cos²θ+2cos 4θ cos θ+sin²4 θ + sin² θ+2sin4 θ sin θ

= 2+2(cos4θ cos θ+sin4 θ sin θ)

= 2+2 cos3 θ

At θ = π/5,

det B = 2+2 cos3×π/5

= 2(1-sin 18)

= 2(1-(√5-1)/4)

= 2(5-√5)/4)

= (5-√5)/2

lies in (1,2)

Answer: (2)

13. The centre of the circle passing through the point (0,1) and touching the parabola y = x² at the point (2,4) is :

1) (3/10, 16/5)
2) (6/5, 53/10)
3) (-16/5, 53/10)
4) (-53/10, 16/5)

Circle passing through point (0,1) and touching curve y = x² at (2,4)

tangent at (2,4) is (y+4)/2 = x(2)

⇒ y-4x+4 = 0

Equation of circle

(x-2)² +(y-4)²+λ(4x-y-4) = 0

Passing through (0,1) 4+9 +λ(-5) = 0

λ = 13/5

Circle is

x²-4x+4+y²-8y+16+(13/5)(4x-y-4) = 0

x²+y²+((52/5)-4)x-(8+13/5)y+20-(52/5) = 0

x²+y²+(32/5)x-(53/5)y+(48/5) = 0

centre is (-16/5, 53/10)

Answer: (3)

14. A plane P meets the coordinate axes at A, B and C respectively. The centroid of a triangle ABC is given to be (1,1,2). Then the equation of the line through this centroid and perpendicular to the plane P is:

1) (x-1)/2 = (y-1)/1 = (z-2)/1
2) (x-1)/2 = (y-1)/2 = (z-2)/1
3) (x-1)/1 = (y-1)/2 = (z-2)/2
4) (x-1)/1 = (y-1)/1 = (z-2)/2

G = (α/3, β/3,

α = 3, β = 3,

Equation of plane is

(x/α)+(y/β)+(z/

(x/3)+(y/3)+(z/6) = 1

2x+2y+z = 6

Required line perpendicular to plane is (x-1)/2 = (y-1)/2 = (z-2)/1

Answer: (2)

15. Let f : R→ R be a function defined by f(x) = max {x,x²}. Let S denote the set of all points in R, where f is not differentiable. Then

1) {0,1}
2) an empty set
3) {1}
4) {0}

Function is not differentiable at two point {0,1}.

Answer: (1)

16. The angle of elevation of the summit of a mountain from a point on the ground is 45⁰. After climbing up one km towards the summit at an inclination of 30⁰ from the ground, the angle of elevation of the summit is found to be 60⁰. Then the height (in km) of the summit from the ground is:

If ΔCDF

Sin 30⁰ = z/1

Z = ½ Km

Cos 30⁰ = y/1

y = √3/2 Km

Now in ABC

tan 45⁰ = h/(x+y)

⇒ h = x+y

Or x = h -√3/2

Now, in ΔBDE

tan 60⁰ = (h-z)/x

After substituting the value of x, we get

h = 1/ (√3-1) Km

Answer: (1)

17. If the constant term in the binomial expansion of (√x – k/x²)¹⁰ is 405, then |k| equals:

1) 1
2) 9
3) 2
4) 3

¹⁰C_r (-k/x²)^r (√x)^10-r

¹⁰C_r (-k)^r (x)^5-5r/2

For constant term

5-5r/2 = 0

Or r = 2

Now, T₃ = ¹⁰C₂ k² = 405

Or k² = 405/45 = 9

Or |k| = 3

Answer: (4)

18. Let z = x+iy be a non-zero complex number such that z² = i|z|², where i = √-1 , then z lies on the

1) line, y = x
2) real axis
3) imaginary axis
4) line, y = -x

z² = i |z|²

x²-y²+2i xy = i(x²+y²)

equating real terms

x²-y² = 0

⇒ x² = y²

equating imaginary terms

2xy = x²+y²

(x-y)² = 0

⇒ x = y

Answer: (1)

19. Let L denote the line in the xy-plane with x and y intercepts as 3 and 1 respectively. Then the image of the point (-1, -4) in this line is:

1) (11/5, 28/5)
2) (8/5, 29/5)
3) (29/5, 11/5)
4) (29/5, 8/5)

Let (h, k) is the image of the point (-1, -4) in the line

x/3 + y/1 = 1

x+3y = 3

L2: 3x-y + λ = 0

-3+4+λ = 0

λ = -1

3x-y = 1

(h,k) satisfy the equation of line L2

3h-k = 1 …(1)

16 = |h+3k-3|

h +3k = 19 …(2)

h +3k = -13 …(3)

From equation (2) and (3), put value of h in (1)

h = 19-3k,

3(19 -3k) -k=1

-10k = -56 = 28/5

k = 28/5

h = 19-3(28/5) = 11/5

h = -13-3k

3(-13-3k) -k=1

-10k = 40

k = -4

Image = (11/5, 28/5)

Answer: (1)

20. Consider the statement : “For an integer n, if n³-1 is even, then n is odd.” The contrapositive statement of this statement is:

1) For an integer n, if n is even, then n³-1 is even
2) For an integer n, if n is odd, then n³-1 is even
3) For an integer n, if n³-1 is not even, then n is not odd.
4) For an integer n, if n is even, then n³-1 is odd

P:n³-1 is even, q : n is odd

Contrapositive of p →q = ∼q → ∼p

⇒ If n is not odd then n³-1 is not even

⇒ For an integer n, if n is even, then n³-1 is odd

Answer: (4)

21. The number of words (with or without meaning) that can be formed from all the letters of the word “LETTER” in which vowels never come together is:

Consonants → LTTR

Vowels → EE

Total No of words = 6!/(2!2!)

= 180 (T and E repeated)

Total no of words if vowels are together

= 5!/2!

= 60 (E is repeated)

Required = 180-60 = 120

Answer: 120

22. If

⇒

And

⇒

by comparing (i) and (ii)

we get λ = 1

Answer: 1

23. Consider the data on x taking the values 0, 2, 4, 8, …..,2n with frequencies ⁿC₀, ⁿC₁, ⁿC_2… ⁿC_n, respectively. If the mean of this data is 728/2ⁿ, then n is equal to:

3ⁿ = 729 = 3⁶

n = 6

Answer: 6

24. Suppose that function f : R→R satisfies f(x+y) = f(x)f(y) for all x, y∈R and f(1) = 3. If

f(x+y) = f(x) f(y)

f(x) = a^x

f(1) = a = 3

So f(x) = 3^x

⇒ 3+3²+3³+….+3ⁿ = 363

⇒ 3(3ⁿ-1)/2 = 363

⇒ n = 5

Answer: 5

25. The sum of distinct values of λ for which the system of equations

(λ-1)x+(3λ+1)y+2λz = 0

(λ-1)x+(4λ-2)y+(λ+3)z = 0

2x+(3λ+1)y+3(λ-1)z = 0 has non-zero solutions, is:

R₂ → R₂-R₁

R₃ → R₃-R₁

C₁ → C₁ + C₃

(λ-3)[(3λ-1)(λ-3)-3(3-λ)(3λ+1)] = 0

(λ-3)[3λ²-10λ+3-(8λ-3λ²+3)] = 0

(λ-3)(6λ²-18λ) = 0

(6λ)(λ-3)² = 0

λ = 0, 3

Sum of the values of λ = 0+3 = 3

Answer: 3