The JEE Main 2022 July 28 – Shift 2 Physics Question Paper with Solutions is given on this page. Solving the JEE Main 2022 question papers will definitely help students to understand the exam pattern and difficulty level. They can use the JEE Main 2022 answer keys to assess their performance. JEE Main 2022 question paper with solutions contains well-explained and accurate solutions prepared by a team of experts at BYJU’S. Revise the JEE Main 2022 July 28 – Shift 2 Physics Question Paper with Solutions given below.
JEE Main 2022 July 28th Shift 2 Physics Question Paper and Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. Consider the efficiency of Carnot engine is given by \(\begin{array}{l} \eta=\frac{\alpha\beta}{\sin\theta}\text{log}_e\frac{\beta~x}{kT},\end{array} \)
where α and β are constants. If T is temperature, k is Boltzmann constant,θ is angular displacement, and x has the dimensions of length. Then, choose the incorrect option
\(\begin{array}{l}\left(A\right) \text{Dimensions of}~ \beta~ \text{is same as that of force}.\\ \left(B\right) \text{Dimensions of} ~\alpha^{-1}x~ \text{is same as that of energy.}\\ \left(C\right)\text{Dimensions of}~ \eta^{-1}sin~\theta~ \text{is same as that of} ~\alpha \beta.\\ \left(D\right) \text{Dimensions of} ~\alpha ~\text{is same as that of }\beta.\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l} (\text{A})\ \left[\beta\right]=\left[\frac{kT}{x}\right]=\left[\frac{E}{x}\right]=\left[MLT^{-2}\right] = \left[F\right] \end{array} \)
\(\begin{array}{l}\left(B\right)\left[\alpha \beta\right] = \left[M^0L^0T^0\right]\end{array} \)
\(\begin{array}{l} \left[\alpha\right]^{-1}=\left[\beta\right]=\left[\frac{KT}{x}\right]\end{array} \)
\(\begin{array}{l}So \left[\alpha\right]^{-1}\left[x\right] = \left[kT\right] = \left[ML^2T^{-2}\right]\end{array} \)
\(\begin{array}{l}\left(C\right) \eta sin \theta = \alpha \beta\\ So \left[\eta sin\theta \right] = \left[\alpha \beta\right] \end{array} \)
\(\begin{array}{l}\left[\eta\right] = \left[M^0L^0T^0\right] \text{it is dimensionless quantity}\end{array} \)
\(\begin{array}{l}\left(D\right) \left[ \alpha\right] \neq \left[\beta\right]\end{array} \)
2. At time t = 0 a particle starts travelling from a height \(\begin{array}{l}7\hat{z}\ cm\ \text{in a plane keeping z coordinate constant}.\end{array} \)
At any instant of time it’s position along the \(\begin{array}{l} \hat{x}\ \text{and}\ \hat{y}\ \text{directions are defined at}\ 3t\ \text{and}\ 5t^3\ \text{respectively}.\end{array} \)
At t = 1 s acceleration of the particle will be
\(\begin{array}{l} (\text{A})\ -30\hat{y} \end{array} \)
\(\begin{array}{l} (\text{B})\ 30\hat{y} \end{array} \)
\(\begin{array}{l} (\text{C})\ 3\hat{x}+15\hat{y}\end{array} \)
\(\begin{array}{l} (\text{D})\ 3\hat{x}+15\hat{y}+7\hat{z}\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l} x = 3t \Rightarrow a_x = 0\\ y = 5t^3 \Rightarrow a_y = 30t\end{array} \)
\(\begin{array}{l} \overrightarrow{a}\left(t=1\right)=30\hat{y} \end{array} \)
3. A pressure-pump has a horizontal tube of cross sectional area 10 cm2for the outflow of water at a speed of 20 m/s. The force exerted on the vertical wall just in front of the tube which stops water horizontally flowing out of the tube, is
[given: density of water = 1000 kg/m3]
(A) 300 N
(B) 500 N
(C) 250 N
(D) 400 N
Answer (D)
Sol.
\(\begin{array}{l}F_w = \rho Av^2\\ = 10^3 \times 10 \times 10^{-4} \times 20 \times 20\\ = 400 \text{N}\end{array} \)
4. A uniform metal chain of mass m and length ‘L’ passes over a massless and frictionless pully. It is released from rest with a part of its length ‘l’ is hanging on one side and rest of its length ‘L – l’ is hanging on the other side of the pully. At a certain point of time, when l = L/x, the acceleration of the chain is g/2. The value of x is ______.
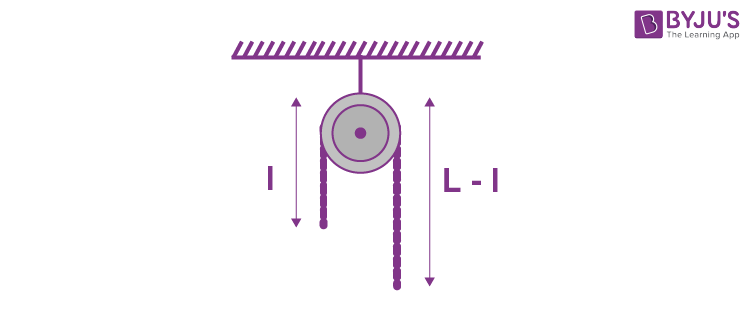
(A) 6
(B) 2
(C) 1.5
(D) 4
Answer (D)
Sol.
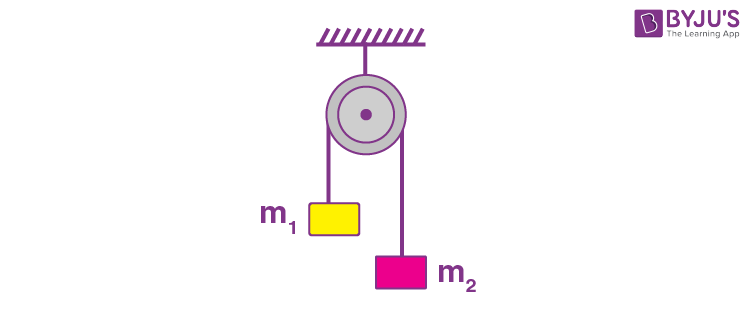
\(\begin{array}{l} a=\frac{m_2-m_1}{m_1+m}g=\frac{g}{2} \end{array} \)
\(\begin{array}{l}\Rightarrow m_2 = 3m_1\\ \left(L – l\right) = 3l\\ L = 4l\end{array} \)
\(\begin{array}{l} l=\frac{L}{4}\end{array} \)
5. A bullet of mass 200 g having initial kinetic energy 90 J is shot inside a long swimming pool as shown in the figure. If it’s kinetic energy reduces to 40 J within 1 s, the minimum length of the pool, the bullet has to travel so that it completely comes to rest is

(A) 45 m
(B) 90 m
(C) 125 m
(D) 25 m
Answer (A)
Sol.
\(\begin{array}{l} \frac{1}{2}mx^2=90 \end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{1}{2}\times0.2\times x^2=90 \end{array} \)
x2 = 900
x = 30 m/s
\(\begin{array}{l} \frac{1}{2}mv^2=40\Rightarrow v=\frac{2}{3}\times30=20 \text{ m/s}\end{array} \)
\(\begin{array}{l}20 = 30 – a \times 1 \Rightarrow a = -10 ~\text{m/s}^2\\ 0 – x^2 = 2as\end{array} \)
\(\begin{array}{l} s=\frac{x^2}{-2a}=\frac{30\times30}{2\times 10}= 45 ~\text{m}\end{array} \)
6. Assume there are two identical simple pendulum clocks. Clock – 1 is placed on the earth and Clock -2 is placed on a space station located at a height h above the Earth surface. Clock – 1 and Clock – 2 operate at time periods 4 s and 6 s, respectively. Then the value of h is-
(consider radius of earth RE = 6400 km and g on earth 10 m/s2)
(A) 1200 km
(B) 1600 km
(C) 3200 km
(D) 4800 km
Answer (C)
\(\begin{array}{l} T\propto \sqrt{1/g}\end{array} \)
\(\begin{array}{l} \Rightarrow \frac{T_1}{T_2}=\sqrt{\frac{g_2}{g_1}}=\frac{R}{R+h}\end{array} \)
\(\begin{array}{l} \frac{4}{6}=\frac{R}{R+h}\end{array} \)
\(\begin{array}{l}\Rightarrow h = R/2\\ = 3200~ \text{km}\end{array} \)
7. Consider a cylindrical tank of radius 1 m is filled with water. The top surface of water is at 15 m from the bottom of the cylinder. There is a hole on the wall of cylinder at a height of 5 m from the bottom. A force of 5 × 105 N is applied an the top surface of water using a piston. The speed of ifflux from the hole will be:
(given atmosphere pressure
\(\begin{array}{l}P_A = 1.01 \times 10^5~\text{Pa} \end{array} \)
, density of water \(\begin{array}{l}\rho_w = 1000 ~\text{kg/m}^3\end{array} \)
and gravitational acceleration g = 10 m/s2)
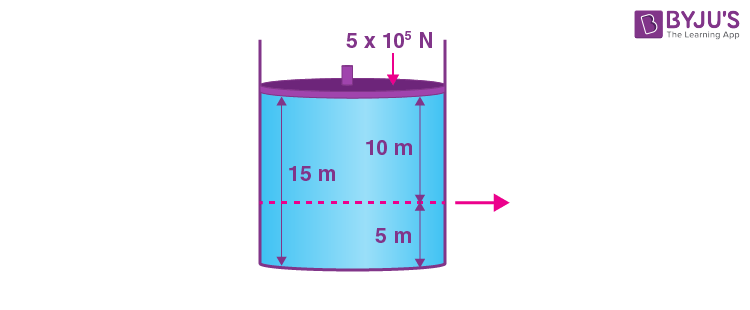
(A) 11.6 m/s
(B) 10.8 m/s
(C) 17.8 m/s
(D) 14.4 m/s
Answer (C)
Sol. By Bernoulli’s theorem,
\(\begin{array}{l} \frac{5\times10^5}{\pi\left(1\right)^2}+\rho g\left(10\right) =1.01\times10^5+\frac{1}{2}\rho\left(v\right)^2\end{array} \)
\(\begin{array}{l} \Rightarrow v^2=200+\frac{10^6}{1000\pi}-202 \end{array} \)
\(\begin{array}{l}\Rightarrow v \simeq 17.8~ \text{m/s}\end{array} \)
8. A vessel contains 14 g of nitrogen gas at a temperature of 27°C. The amount of heat to be transferred to the gas to double the r.m.s speed of its molecules will be:
\(\begin{array}{l}\text{Take} ~R = 8.32~ \text{J~mol}^{-1}\text{K}^{-1}.\end{array} \)
(A) 2229 J
(B) 5616 J
(C) 9360 J
(D) 13,104 J
Answer (C)
Sol. n = 0.5
T = 300
For vrms to be doubled T′ = 4 × 300 = 1200
⇒ Heat transferred
\(\begin{array}{l} =\left(0.5\right)\left(\frac{5}{2}\right)\left(8.32\right)\left(900\right)\\ = 9360 ~\text{J} \end{array} \)
9. A slab of dielectric constant K has the same cross-sectional area as the plates of a parallel plate capacitor and thickness (3/4)d, where d is the separation of the plates. The capacitance of the capacitor when the slab is inserted between the plates will be:
(Given C0 = capacitance of capacitor with air as medium between plates.)
\(\begin{array}{l} (\text{A})\ \frac{4KC_0}{3+K}\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{3KC_0}{3+K}\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{3+K}{4KC_0}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{K}{4+K}\end{array} \)
Answer (A)
Sol.
\(\begin{array}{l} C_0=\frac{\varepsilon_0A}{d}\end{array} \)
\(\begin{array}{l} C=\frac{\varepsilon_0A}{d-\frac{3d}{4}+\frac{3d}{4K}}=\frac{4\varepsilon_0AK}{3d+Kd}\end{array} \)
\(\begin{array}{l} =\frac{4KC_0}{3+K}\end{array} \)
10. A uniform electric field E = (8m/e) V/m is created between two parallel plates of length 1 m as shown in figure, (where m = mass of electron and e = charge of electron). An electron enters the field symmetrically between the plates with a speed of 2 m/s. The angle of the deviation (θ) of the path of the electron as it comes out of the field will be_______.
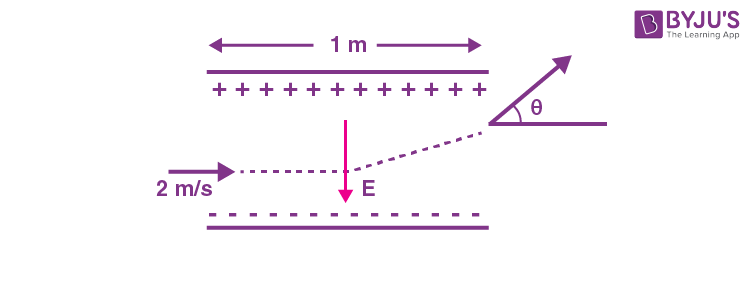
\(\begin{array}{l} \left(A\right) tan^{-1}(4)\\ \left(B\right) tan^{-1}(2)\\ \left(C\right) \tan^{-1}\left(\frac{1}{3}\right)\\ \left(D\right) tan^{-1} (3)\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l} E=\frac{8\ m}{e}\text{V/m} \end{array} \)
\(\begin{array}{l} l = 1 ~\text{m}\\ v_x = 2~ \text{m/s}\\ a_y = – 8 ~\text{m/s}^2\end{array} \)
\(\begin{array}{l} t=\frac{l}{v_x}=\frac{1}{2}\text{ s}\end{array} \)
\(\begin{array}{l}\Rightarrow \left|v_y\right| = 4 \text{m/s}\\ \Rightarrow \text{angle of deviation} = \theta \end{array} \)
\(\begin{array}{l} \tan \theta =\frac{v_y}{v_x}\end{array} \)
\(\begin{array}{l} \theta = \tan^{-1}\left(\frac{4}{2}\right)=\tan^{-1}\left(2\right) \end{array} \)
11. Given below are two statements:
Statement I : A uniform wire of resistance 80 Ω is cut into four equal parts. These parts are now connected in parallel. The equivalent resistance of the combination will be 5 Ω.
Statement II : Two resistances 2R and 3R are connected in parallel in a electric circuit. The value of thermal energy developed in 3R and 2R will be in the ratio 3 : 2.
In the light of the above statements, choose the most appropriate answer from the option given below.
(A) Both statement I and statement II are correct
(B) Both statement I and statement II are incorrect
(C) Statement I is correct but statement II is incorrect
(D) Statement I is incorrect but statement II is correct
Answer (C)
Sol. Statement I :
\(\begin{array}{l} R_{1 \text{ part}} =\frac{80}{4}=20\ \Omega\end{array} \)
\(\begin{array}{l} \Rightarrow R_\text{eff}=\frac{20}{4}=5~\Omega\end{array} \)
Statement II :
\(\begin{array}{l} \text{Ratio}=\frac{\frac{\left(\Delta V\right)^2}{3R}}{\frac{\left(\Delta V\right)^2}{2R}}\end{array} \)
\(\begin{array}{l} =\frac{2}{3} \end{array} \)
12. A triangular shaped wire carrying 10 A current is placed in a uniform magnetic field of 0.5 T, as shown in figure. The magnetic force on segment CD is (Given BC = CD = BD = 5 cm).
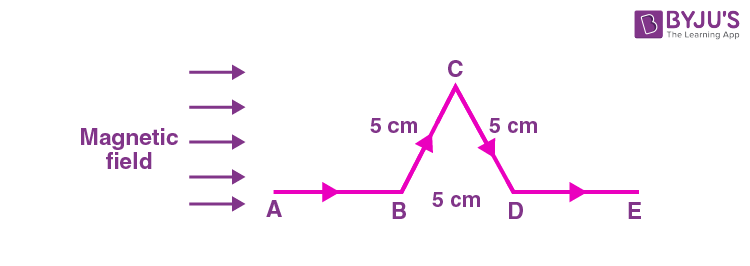
(A) 0.126 N
(B) 0.312 N
(C) 0.216 N
(D) 0.245 N
Answer (C)
Sol.
\(\begin{array}{l}\overrightarrow{F}=i\overrightarrow{\ell}\times \overrightarrow{B}\\= ilB~sin~60^\circ\end{array} \)
\(\begin{array}{l}=10\times \frac{5}{100}\times0.5\times\frac{\sqrt{3}}{2}\end{array} \)
=0.2165 N
13. The magnetic field at the center of current carrying circular loop is B1. The magnetic field at a distance of √3 times radius of the given circular loop from the center on its axis is B2. The value of B1/B2 will be
(A) 9 : 4
(B) 12 : √5
(C) 8 : 1
(D) 5 : √3
Answer (C)
Sol.
\(\begin{array}{l} B_1=\frac{\mu_0i}{2R} \end{array} \)
\(\begin{array}{l} B_2=\frac{\mu_0iR^2}{2\left(R^2+x^2\right)^\frac{3}{2}} \end{array} \)
\(\begin{array}{l} \Rightarrow \frac{B_1}{B_2}=\frac{1}{R^3}\left(R^2+x^2\right)^\frac{3}{2}\end{array} \)
\(\begin{array}{l} =\frac{1}{R^3}\left(8R^3\right)\\= 8 \end{array} \)
14. A transformer operating at primary voltage 8 kV and secondary voltage 160 V serves a load of 80 kW. Assuming the transformer to be ideal with purely resistive load and working on unity power factor, the loads in the primary and secondary circuit would be
\(\begin{array}{l}\left(A\right) 800 ~\Omega ~\text{and}~ 1.06 ~\Omega \\\left(B\right)10~ \Omega ~\text{and}~ 500 ~\Omega\\ \left(C\right)800 ~\Omega ~\text{and}~ 0.32~ \Omega \\\left(D\right) 1.06 ~\Omega~\text{and}~ 500 ~\Omega\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l} V_1i_1=V_2i_2=80\ \text{kW}\end{array} \)
\(\begin{array}{l} \Rightarrow\ i_1=10 \text{ A and }i_2=\frac{80\times1000}{160}=500\text{ A}\end{array} \)
\(\begin{array}{l} \Rightarrow R_1=\frac{V_1}{i_1}=800\ \Omega \text{ and }R_2=\frac{160}{500}=0.32\ \Omega\end{array} \)
15. Sun light falls normally on a surface of area 36 cm2 and exerts an average force of 7.2 × 10–9 N within a time period of 20 minutes. Considering a case of complete absorption, the energy flux of incident light is
\(\begin{array}{l}\left(A\right) 25.92 \times 10^2 ~\text{W/cm}^2\\ \left(B\right)8.64 \times 10^{-6}~\text{W/cm}^2\\ \left(C\right) 6.0 ~\text{W/cm}^2\\ \left(D\right)0.06 ~\text{W/cm}^2\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l} \text{Pressure}=\frac{I}{c} \end{array} \)
\(\begin{array}{l} \Rightarrow \frac{F}{A}=\frac{I}{c}\end{array} \)
\(\begin{array}{l} \Rightarrow l=\frac{7.2\times10^{-9}\times3\times10^8}{36\times10^{-4}}\text{W/m}^2 \\= 600 ~\text{W/m}^2\end{array} \)
\(\begin{array}{l} \Rightarrow I=0.06\text{ W/cm}^2 \end{array} \)
16. The power of a lens (biconvex) is 1.25 m–1 in particular medium. Refractive index of the lens is 1.5, and the radii of curvature are 20 cm and 40 cm, respectively. The refractive index of surrounding medium
\(\begin{array}{l} (\text{A})1.0 \end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{9}{7} \end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{3}{2} \end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{4}{3} \end{array} \)
Answer (B)
Sol.
\(\begin{array}{l} \because \frac{1}{f}=\left(\frac{\mu_2}{\mu_1}-1\right)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{1.25}{100}=\left(\frac{1.5}{\mu_1}-1\right)\left(\frac{1}{20}+\frac{1}{40}\right)\end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{1}{80}=\left(\frac{1.5}{\mu_1}-1\right)\times \frac{\left(4+2\right)}{80}\end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{1.5}{\mu_1}-1=\frac{1}{6}\end{array} \)
\(\begin{array}{l} \Rightarrow \frac{1.5}{\mu_1}=\frac{7}{6}\end{array} \)
\(\begin{array}{l} \Rightarrow \mu_1=\frac{1.5\times6}{7}=\frac{9}{7}\end{array} \)
17. Two streams of photons, possessing energies equal to five and ten times the work function of metal are incident on the metal surface successively. The ratio of maximum velocities of the photoelectron emitted, in the two cases respectively, will be
(A) 1 : 2
(B) 1 : 3
(C) 2 : 3
(D) 3 : 2
Answer (C)
Sol.
\(\begin{array}{l} \frac{1}{2}mv_1^2=5\phi-\phi\end{array} \)
And,
\(\begin{array}{l} \frac{1}{2}mv_2^2=10\phi-\phi \end{array} \)
\(\begin{array}{l} \Rightarrow \left(\frac{v_1}{v_2}\right)^2=\frac{4}{9} \end{array} \)
\(\begin{array}{l} \Rightarrow \frac{v_1}{v_2}=\frac{2}{3}\end{array} \)
18. A radioactive sample decays 7/8 times its original quantity in 15 minutes. The half-life of the sample is
(A) 5 min
(B) 7.5 min
(C) 15 min
(D) 30 min
Answer (A)
Sol.
\(\begin{array}{l} N=\frac{N_0}{2^{\frac{t}{T_{1/2}}}}\end{array} \)
\(\begin{array}{l} \Rightarrow 2^{\frac{t}{T_{1/2}}} =\frac{N_0}{N}=\frac{N_0}{\left(\frac{N_0}{8}\right)}=8\end{array} \)
\(\begin{array}{l} \Rightarrow \frac{t}{T_{1/2}}=3\end{array} \)
\(\begin{array}{l} \Rightarrow T_{1/2}=\frac{15}{3}=5\text{ min}\end{array} \)
19. An npn transistor with current gain β = 100 in common emitter configuration is shown in the figure. The output voltage of the amplifier will be
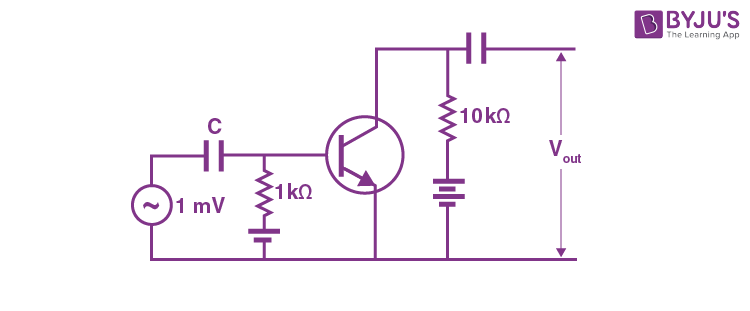
(A) 0.1 V
(B) 1.0 V
(C) 10 V
(D) 100 V
Answer (B)
Sol.
\(\begin{array}{l}\Rightarrow \frac{V_0}{V_i}=\beta\times\left(\frac{R_C}{R_B}\right)\end{array} \)
\(\begin{array}{l} \Rightarrow V_0=100\times\left(\frac{10}{1}\right)\times10^{-3}\\= 1.0~ \text{V}\end{array} \)
20. A FM Broad cast transmitter, using modulating signal of frequency 20 kHz has a deviation ratio of 10. The Bandwidth required for transmission is
(A) 220 kHz
(B) 180 kHz
(C) 360 kHz
(D) 440 kHz
Answer (D)
Sol.
\(\begin{array}{l}\text{Band width of FM wave} = 2\left(\triangle f + f_m\right)\\ \frac{\Delta f}{f_m}=10~~~~~~~~\left(Given\right)\\ \Delta f = f_m(10) = 20 \times 10 = 200 ~\text{kHz}\\ BW = 2\left(200 + 20\right) ~\text{kHz}\\ = 440 ~\text{kHz}\end{array} \)
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, –00.33, –00.30, 30.27, –27.30) using the mouse and the on-screen virtual numeric keypad in the place designated to enter the answer.
1. A ball is thrown vertically upwards with a velocity of 19.6 ms–1 from the top of a tower. The ball strikes the ground after 6 s. The height from the ground up to which the ball can rise will be (k/5) m. The value of k is ______ (use g = 9.8 m/s2)
Answer (392)
Sol. v = 19.6 m/s
t = 6s
Time taken in upward motion above tower = 2s
⇒ Time taken from top most point to ground = 4s
\(\begin{array}{l} \Rightarrow\ \sqrt{\frac{2h}{g}}=4\end{array} \)
\(\begin{array}{l} h=\frac{16\times9.8}{2}=8\times9.8 \end{array} \)
\(\begin{array}{l}\Rightarrow k = 8 \times 9.8 \times 5 = 392\end{array} \)
2. The distance of centre of mass from end A of a one dimensional rod (AB) having mass density \(\begin{array}{l} \rho=\rho_0\left(1-\frac{x^2}{L^2}\right)\text{ kg/m}\ \text{and length}\ L\ (\text{in meter})\ \text{is}\ \frac{3L}{\alpha}\text{ m}.\end{array} \)
The value ofαis ______. (where x is the distance from end A)
Answer (8)
Sol.
\(\begin{array}{l} \rho=\rho_0\left(1-\frac{x^2}{L^2}\right)\text{ kg/m} \end{array} \)
\(\begin{array}{l} x_\text{cm}=\frac{A\displaystyle\int\limits_0^L\rho_0\left(1-\frac{x^2}{L^2}\right)x\ dx}{A\displaystyle\int\limits_0^L\rho_0\left(1-\frac{x^2}{L^2}\right)dx}\end{array} \)
\(\begin{array}{l} x_{cm}=\frac{\frac{L^2}{2}-\frac{L^2}{4}}{L-\frac{L}{3}}=\frac{\frac{L^2}{4}}{\frac{2L}{3}}=\frac{3L}{8} \end{array} \)
\(\begin{array}{l}\Rightarrow \alpha = 8\end{array} \)
3. A string of area of cross-section 4mm2 and length 0.5 m is connected with a rigid body of mass 2 kg. The body is rotated in a vertical circular path of radius 0.5 m. The body acquires a speed of 5 m/s at the bottom of the circular path. Strain produced in the string when the body is at the bottom of the circle is ______×10–5.
(use young’s modulus 1011 N/m2 and g = 10 m/s2)
Answer (30)
Sol.
\(\begin{array}{l}A = 4 \times 10^{-6} ~\text{m}^2\\ l = 0.5 ~\text{m}\\ m = 2 ~\text{kg}\\ v_b= 5 ~\text{m/s}\end{array} \)
\(\begin{array}{l} T_b=mg+m\left(\frac{V_b^2}{l}\right) \end{array} \)
\(\begin{array}{l} =20+2\times\frac{25}{\frac{1}{2}}=120\text{ N}\end{array} \)
\(\begin{array}{l} \frac{\Delta l}{l}=\frac{T_b}{A}\times \frac{1}{Y}=\frac{120}{4\times10^{-6}}\times10^{-11}=30\times 10^{-5} \end{array} \)
4. At a certain temperature, the degrees of freedom per molecule for gas is 8. The gas performs 150 J of work when it expands under constant pressure. The amount of heat absorbed by the gas will be ______ J.
Answer (750)
Sol.
\(\begin{array}{l}f = 8\\ W = P dV = 150\\ Q = W + \Delta U\\ =P dV+\frac{f}{2}PdV\\ Q = 5 \times 150 = 750 ~\text{J}\end{array} \)
5. The potential energy of a particle of mass 4 kg in motion along the x-axis is given by U = 4 (1–cos 4x) J. The time period of the particle for small oscillation \(\begin{array}{l} \left(\sin\theta\simeq\theta\right)\text{ is }\left(\frac{\pi}{K}\right)\text{ s}.\end{array} \)
The value of K is ______.
Answer (2)
Sol.
\(\begin{array}{l}U = 4\left(1 – cos ~4x\right)\end{array} \)
\(\begin{array}{l}\Rightarrow F=-\frac{dU}{dx}=-\left(4\right)\left(4 \sin 4x\right)\\ = -16 sin 4x\end{array} \)
As small x
F = -16(4x) = -64x = -kx
\(\begin{array}{l} T=2\pi\sqrt{\frac{m}{k}}=2\pi\sqrt{\frac{4}{64}}=\frac{\pi}{2} \end{array} \)
\(\begin{array}{l}\Rightarrow K = 2\end{array} \)
6. An electrical bulb rated 220 V, 100 W, is connected in series with another bulb rated 220 V, 60 W. If the voltage across combination is 220 V, the power consumed by the 100 W bulb will be about ____ W.
Answer (14)
Sol.
\(\begin{array}{l} P_{100}=\frac{V^2}{R_{100}}\Rightarrow R_{100}=\frac{V^2}{P_{100}} \end{array} \)
\(\begin{array}{l} P_{60}=\frac{V^2}{R_{60}}\Rightarrow R_{60}=\frac{V^2}{P_{60}}\end{array} \)
\(\begin{array}{l} P_{\text{net}}=\frac{V^2}{R_{60}+R_{100}}=\frac{P_{60}P_{100}}{P_{60}+P_{100}}=\frac{60\times100}{160}=37.5\end{array} \)
This power developed is proportional to resistance.
So,
\(\begin{array}{l} P’_{60}=P_\text{net}\times \frac{60}{160}=37.5\times\frac{60}{160}\simeq 14 \text{ W}\end{array} \)
7. For the given circuit the current through battery of 6 V just after closing the switch S will be _____ A.
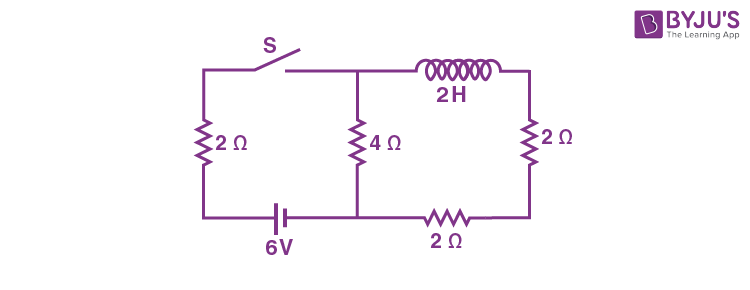
Answer (1)
Sol. Just after closing the switch,
\(\begin{array}{l} i=\frac{6}{4+2}=1\text{ A}\end{array} \)
8. An object O is placed at a distance of 100 cm in front of a concave mirror of radius of curvature 200 cm as shown in the figure. The object starts moving towards the mirror at a speed 2 cm/s. The position of the image from the mirror after 10 s will be at ____ cm.
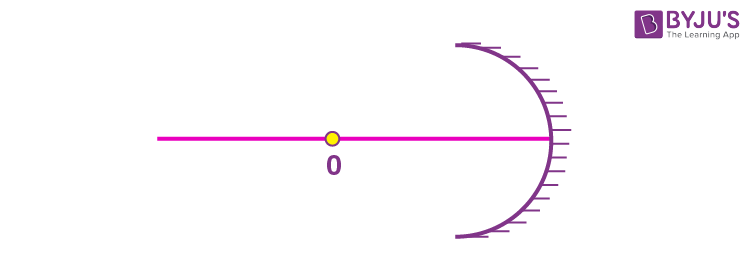
Answer (400)
Sol. The object after 10 second will be at u = –80 cm.
So
\(\begin{array}{l} \frac{1}{v}-\frac{1}{80}=-\frac{1}{100}\Rightarrow v=\frac{8000}{+20}=400\text{ cm} \end{array} \)
9. In an experiment with a convex lens, the plot of the image distance (ν′) against the object distance (μ′) measured from the focus gives a curve ν′μ′ = 225. If all the distances are measured in cm. The magnitude of the focal length of the lens is _______ cm.
Answer (15)
Sol. Using Newton’s formula for lenses,
\(\begin{array}{l}v’ \mu’ = f^2 = 225 \Rightarrow f= 15\end{array} \)
10. In an experiment to find acceleration due to gravity (g) using simple pendulum, time period of 0.5 s is measured from time of 100 oscillations with a watch of 1 s resolution. If measured value of length is
10 cm known to 1 mm accuracy, the accuracy in the determination of g is found to be x %. The value of x is _________ .
Answer (5)
Sol.
\(\begin{array}{l} T=2\pi\sqrt{\frac{l}{g}} \end{array} \)
\(\begin{array}{l} \frac{dg}{g}\times100=\frac{2dT}{T}\times 100+\frac{d\ell}{\ell}\times100\end{array} \)
\(\begin{array}{l} =2\times\frac{1}{50}\times100+\frac{1}{100}\times100=5\%\end{array} \)
JEE Main 2022 July 28th Shift 2 Paper Analysis


















Comments