a. 2√5
b. 2√7
c. 2√2
d. 4
3x+4y =12√2 is a tangent to the ellipse (x2/a2) + (y2/9) = 1
Equation of tangent to ellipse (x2/a2) + (y2/9) = 1 is y = mx + √(a2 m2+ 9)
Now, 3x + 4y = 12√2 ⇒ y = -(3/4)x + 3√2
m = -3/4
And √(a2 m2+ 9) = 3√2
(a2 (-3/4)2+ 9) = 18
a2 (9/16) = 9
a2 = 16
a = 4
e = √(1-b2/a2)
e = √(1-9/16)
= √7/4
Distance between foci is 2ae = 2 × 4 × √7/4
= 2√7
Answer: (b)
2. Let A, B, C and D be four non-empty sets. The Contrapositive statement of “If A ⊆ B and B ⊆ D
then A ⊆ C ” is :
a. If A ⊆ C, then B ⊂ A or D ⊂ B
b. If A ⊈ C, then A ⊆ B and B ⊆ D
c. If A ⊈ C, then A ⊈ B and B ⊆ D
d. If A ⊈ C, then A ⊈ B or B ⊈ D
Given statements: A ⊆ B and B ⊆ D
Let A ⊆ B be p
B ⊆ D be q
A ⊆ C be r
Modified statement: (p
Contrapositive: ~r ⇒ ~ (p
~r ⇒ (~p
A ⊈ C, then A ⊈ B or B ⊈ D
Answer: (d)
a. 420
b. 330
c. 210
d. 120
Coefficient of x7 in (1+x)10+ x(1+x)9+ x2(1+x)8+⋯ +x10
Applying sum of terms of G.P =
= (1 + x)11 − x11
Coefficient of x7 ⟹ 11C7 = 330
Answer: (b)
a. 17/2
b. 4
c. 17/4
d. 17/8
P(Machine being faulty) = p = (1/4)
q = ¾
P(at most two machines being faulty)=P(zero machine being faulty)+P(one machine being
faulty)+P(two machines being faulty)
= 5C0 p0q5 + 5C1 p1q4 + 5C2 p2q3
= q5 + 5pq4 + 10p2q3
= (3/4)5 + 5×(1/4)×(3/4)4 + 10(1/4)2×(3/4)3
= (3/4)3[(9/16) + (15/16) + (10/16)]
= (3/4)3× (34/16)
= (3/4)3× (17/8)
k = 17/8
Answer: (d)
a. 2x − 3y = 0
b. 3x − 2y = 0
c. 5x − 7y = 0
d. 7x − 5y = 0

Let R be the midpoint of PQ
PQ is perpendicular on line y = x
Equation of the line PQ can be written as y = −x + c
y = −x+c intersects y = x at Q: (c/2, c/2)
y = −x+c intersects x = 2y at P: (2c/3, c/3)
Midpoint R = (7c/12 , 5c/12)
Locus of R: x = 7c/12, y = 5c/12
5x – 7y = 0
Answer. (c)
a. loge 2
b. loge √2
c. loge (4/3)
d. loge (3/2)
⇒ 4[1 − e−2α − e−α + 1] = 5
Let e−α = t
⇒ 4t2 + 4t − 3 = 0
⇒ t = 1/2 = e−α
⇒ α = log𝑒 2
Answer. (a)
a. 10
b. 25
c. 5
d. 20
S = 3 + 4 + 8 + 9 + 13 + 14 +…..40 terms
S = (3+4)+(8+9)+(13+14)+…..40 terms
S = 7 + 17 + 27 + 37 +….20 terms
This is an AP with a = 7, d = 10
S = (n/2)(2a+(n-1)d)
= (20/2)(14 + (19)10)
= (20/2)204
= 20 × 102
m = 20
Answer.(d)
a. π- tan-1 (4/3)
b. – tan-1 (3/4)
c. π- tan-1 (4/3)
d. tan-1 (4/3)
Let
𝑧 is real.
4 sin 𝜃 + 3 cos 𝜃 = 0
⇒ tan 𝜃 = -3/4 [𝜃 lies in 2𝑛𝑑 quadrant]
arg (sin θ+ i cosθ ) =π + tan-1 (cos 𝜃 /sin 𝜃) =π – tan-1(4/3)
Answer: (a)
a. 1/9
b. 1/81
c. 1/3
d. 3
𝑏𝑖 = (3)(𝑖+𝑗−2)𝑎𝑗𝑖
B =
Taking 32 common each from C3 and R3
Taking 3 common each from C2 and R2
Given ǀBǀ = 81
81 = 81×9 ǀAǀ
ǀAǀ = 1/9
Answer. (a)
a. f(1) –4f(–1) = 4
b. x = 1 is a point of maxima and x = −1 is a point of minimum of f.
c. f is an odd function.
d. x = 1 is a point of minima and x = −1 is a point of maxima of f.
Given
f(x) = ax5 + bx4 + cx3
c = 2
also f’(x) = 5ax4 + 4bx3 + 6x2
f’(1) = 5a + 4b + 6 = 0
f’(-1) = 5a – 4b + 6 = 0
b = 0 and a = -6/5
f(x) = -(6/5)x5 + 2x3
f(x) is odd
f’(x) = -6x4+ 6x2
f’’(x) = -24x3 +12x
(f’’(1) < 0)
(f’’(-1) > 0)
At x = -1 there is local minima and at x = 1 there is local maxima.
And f(1) -4f(-1) = 4
Answer: (d)
a. 4
b. 6
c. 2
d. 3
Using 36Cr+1 = (36/r+1)×35Cr
(36/r+1)×35Cr×(k2-3) = 35Cr×6
k2 – 3 = (r+1)/6
k2 = ((r+1)/6) +3
k∈I
r → Non-negative integer 0 ≤ r ≤ 35
r = 5 ⇒ k = ±2
r = 35 ⇒ k = ±3
No. of ordered pairs (r, k) = 4
Answer: (a)
a. 171
b. 511/3
c. -171
d. -513
a1 + a2 = 4 ⇒ a + ar = 4 ⇒ a(1 + r) = 4
a3 + a4 = 16 ⇒ ar2 + ar3 = 16 ⇒ ar2(1 + r) = 16 ⇒ 4r2 = 16
⇒ r = ±2
If r = 2, a = 4/3
whch is not possible as a1 < 0
If r = −2, a = −4
= (-4)[(-2)9 -1]/-3
= 4/3)(-512-1)
= 4(-171)
λ = -171
Answer: (c)
13. Let a, b,c be three unit vectors such that
a. (3/2, 3a×c)
b. (-3/2, 3c×b)
c. (-3/2, 3a×b)
d. (3/2, 3b×c)
Given a, b,c be three unit vectors.
a + b + c =0
= a.b + b.c + c.a
ǀa + b+cǀ2 = ǀ10ǀ2
ǀaǀ2 + ǀbǀ2 +ǀcǀ2 + 2(a.b + b.c + c.a) = 0
λ= -3/2
Also vector d = a×b + b×c + c×a
vector d = a×b + b×(-a-b) + (-a-b)×a
vector d = a×b + a×b + a×b
vector d = 3(a×b)
Answer: (c)
This curve intersects the x − axis at a point whose abscissa is :
a. 2+e
b. 2
c. 2-e
d. -e
(y2– x)dy/dx = 1
(dx/dy) + x = y2
xey = ∫ y2eydy
x = y2 – 2y + 2 + ce-y
Given y(0) = 1
c = -e
Solution is x = y2 -2y + 2 – e-y+1
the value of x where the curve cuts the x axis will be at x = 2-e
Answer: (c)
a. 2π/3
b. π/3
c. (π/3) + (1/6)
d. π/9
⇒ 2cosec2θ – 2 – 5cosec θ + 4 = 0
⇒2 cosec2θ – 4cosec θ – cosec θ + 2 = 0
⇒ cosec θ= 2 or ½ (not possible)
As θ ε[0,2π),
⇒ θ1 =π /6, θ2 = 5π/6
⇒
= (1/2) [(5π/6)-(π/6)] + (sin 6θ/12) ǀ5π/6 π/6
= π/3
Answer: (b)
a. (p1 + p2 + p3 + p4 + p5) = 26
b. p5 = 11
c. p5 = p2 ⋅ p3
d. p3 = p5 − p4
Given α, β are the roots of x2 − x − 1 = 0
⇒ α + β = 1 & αβ = −1
⇒ α2 = α + 1 & β2 = β + 1
pk = αk−2α2 + βk-2β2
pk = αk−2(α + 1) + βk−2(β + 1)
pk = α k−1 + β k−1 + α k−2 + β k−2
⇒ pk = p k−1 + p k−2
⇒ p3 = p2 + p1 = 4
p4 = p3 + p2 = 7
p5 = p4 + p3 = 11
∴ p5 ≠ p2 ⋅ p3 & p1 + p2 + p3 + p4 + p5 = 26
& p3 = p5 − p4
Answer: (c)
a. 125/3
b. 128/3
c. 124/3
d. 127/3

For point of intersection,
4x2 = 8x + 12
⇒ x2 − 2x − 3 = 0
⇒ x = 3, −1
Area bounded is given by
A = (36 + 36 -36) – (4-12 + 4/3)
= 44 – (4/3)
= 128/3
Answer: (b)
a. (4 – √7)/3
b. 2/3
c. (√7 – 2)/3
d. (4 – √5)/3
LMVT is applicable on f(x) in [0,1], therefore it is continuous and differentiable in [0,1]
Now, f(0) = 11, f(1) = 16
f ′(x) = 3x2 − 8x + 8
f’(c) = (f(1) – f(0))/(1-0)
= (16 – 11)/1
⇒ 3c2 − 8c + 8 = 5
⇒ 3𝑐2 − 8𝑐 + 3 = 0
c = (8±2√7)/6 = (4±√7)/3
As c ∈ (0,1)
We get c = (4 – √7)/3
Answer: (a)
a. -√5/2
b. √5/2
c. -√5/4
d. 2/√5
y√(1 − x2)= k − x√(1 − y2)

Answer: (a)
a. 32/5
b. 64/5
c. 52/5
d. 56/5
x2 + y2 − 8x − 4y + 16 = 0
 (x − 4)2 + (y − 2)2 = 4 ⇒ Centre (4, 2) , radius = 2
(x − 4)2 + (y − 2)2 = 4 ⇒ Centre (4, 2) , radius = 2
OA = 4 = OB
In ∆OBC
tan θ= 4/2 = 2 ⇒ sin θ = 2/√5
In ∆BDC
sin θ= BD/2 ⇒ BD = 4/√5
Length of chord of contact (𝐴𝐵) = 8/√5
Alternative
(𝑙) length of tangent = 4 and (𝑟) radius = 2
⇒Length of chord of contact = 2lr /(√(l2+ r2)
Square of length of chord of contact = 64/5
Answer: (b)
21. If system of linear equations
x + y + z = 6
x + 2y + 3z = 10
3x + 2y + 𝜆z = 𝜇
has more than two solutions, then μ – λ2 is equal to
The system of equations has more than 2 solutions
∴ D = D3 = 0
2 λ− 6 −λ + 9 + 2 − 6 = 0
λ= 1
⇒ μ = 14
So, μ − λ2 = 13
Answer: (13)
Given points (1, 0, 3) and Q (5/3, 7/3, 17/3)
Direction ratios of line L : (α-5/3, 7-7/3, 1-17/3)
= ((3α-5)/3, 14/3, -14/3)
Direction ratios of line PQ : (-2/3, -7/3, -8/3)
As line L is perpendicular to PQ
((3α-5)/3)(-2/3) + (14/3)( -7/3) + (-14/3)(-8/3) = 0
-6α + 10 – 98 + 112 = 0
6α = 24
α= 4
Answer: (4)
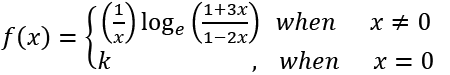
is continuous, then k is equal to
As f(x) is continous
3+2 = k
k = 5
Answer: (5)
Mean = 10
(64 + x + y)/8 = 10
x + y = 80 – 64 = 16
Variance =
25 = ((32 + 72 + 92 + 122 + 132 + 202 + x2 + y2 )/8 )- 100
1000 = 852 + x2 + y2
(x + y)2 – 2xy = 148
256 – 2xy = 148
2xy = 108
So xy = 54
Answer: (54)
A = {x: x is multiple of 2} = {2,4,6,8, … }
B = {x: x is multiple of 7} = {7,14,21, … }
X = {x ∶ 1 ≤ x ≤ 50, x ∈N}
Smallest subset of X which contains elements of both A and B is a set with multiples of 2 or 7 less than 50.
P = {x: x is a multiple of 2 less than or equal to 50}
Q = {x: x is a multiple of 7 less than or equal to 50}
n(P ∪ Q) = n(P) + n(Q) − n(P ∩ Q)
= 25 + 7 − 3
= 29
Answer: (29)
Video Lessons – January 7 Shift 2 Maths




JEE Main 2020 Maths Paper With Solutions Jan 7 Shift 2













Comments