JEE Main 2022 June 28 – Shift 2 Maths Question Paper with Solutions are given on this page. Students can use the JEE Main 2022 answer keys to analyse their performance in the JEE Main 2022 exams. It is highly recommended that they practise the JEE Main 2022 question papers, so that they can improve their speed of cracking the problems. Students can easily access the JEE Main 2022 June 28 – Shift 2 Maths Question Paper with Solutions from our webpage.
JEE Main 2022 June 28th Maths Shift 2 Question Paper and Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. Let R1 = {(a, b) ∈ N × N : |a – b| ≤ 13} and R2 = {(a, b) ∈ N × N : |a – b| ≠ 13}. Then on N:
(A) Both R1 and R2 are equivalence relations
(B) Neither R1 nor R2 is an equivalence relation
(C) R1 is an equivalence relation but R2 is not
(D) R2 is an equivalence relation but R1 is not
Answer (B)
Sol. R1 = {(a, b) ∈ N × N : |a – b| ≤ 13} and
R2 = {(a, b) ∈ N × N : |a – b| ≠ 13}
In R1: ∵ |2 – 11| = 9 ≤ 13
∴ (2, 11) ∈ R1 and (11, 19) ∈ R1 but
(2, 19) ∉ R1
∴ R1 is not transitive
Hence R1 is not equivalence
In R2 : (13, 3) ∈ R2 and (3, 26) ∈ R2 but
(13, 26) ∉ R2 (∵ |13 – 26| = 13)
∴ R2 is not transitive
Hence R2 is not equivalence.
2. Let f(x) be a quadratic polynomial such that f(–2) + f(3) = 0. If one of the roots of f(x) = 0 is –1, then the sum of the roots of f(x) = 0 is equal to:
\(\begin{array}{l}(A)\ \frac{11}{3}\end{array} \)
\(\begin{array}{l}(B)\ \frac{7}{3}\end{array} \)
\(\begin{array}{l}(C)\ \frac{13}{3}\end{array} \)
\(\begin{array}{l}(D)\ \frac{14}{3}\end{array} \)
Answer (A)
Sol. ∵ x = –1 be the roots of f(x) = 0
∴ let f(x) = A(x + 1)(x – b) …(i)
Now, f(–2) + f(3) = 0
⇒ A[–1(–2 – b) + 4(3 – b)] = 0
\(\begin{array}{l}b= \frac{14}{3}\end{array} \)
∴ Second root of f(x) = 0 will be 14/3.
∴ Sum of roots
\(\begin{array}{l}= \frac{14}{3}-1=\frac{11}{3}\end{array} \)
3. The number of ways to distribute 30 identical candies among four children C1, C2, C3 and C4 so that C2 receives atleast 4 and atmost 7 candies, C3 receives atleast 2 and atmost 6 candies, is equal to:
(A) 205
(B) 615
(C) 510
(D) 430
Answer (D)
Sol. By multinomial theorem, no. of ways to distribute 30 identical candies among four children C1, C2 and C3, C4
= Coefficient of x30 in (x4 + x5 + … + x7) (x2 + x3 +…+ x6) (1 + x + x2…)2
\(\begin{array}{l}=\text{Coefficient of}\ x^{24}\ in\ \frac{\left(1-x^{4}\right)}{1-x} \frac{\left(1-x^{5}\right)}{1-x} \frac{\left(1-x^{31}\right)^{2}}{(1-x)^{2}}\end{array} \)
= Coefficient of x24 in (1 – x4 – x5 + x9) (1 – x)–4
= 27C24 – 23C20 – 22C19 + 18C15 = 430
4. The term independent of x in the expansion of \(\begin{array}{l}\left(1-x^{2}+3 x^{3}\right)\left(\frac{5}{2} x^{3}-\frac{1}{5 x^{2}}\right)^{11}, x \neq 0\end{array} \)
is:
\(\begin{array}{l}(A)\ \frac{7}{40}\end{array} \)
\(\begin{array}{l}(B)\ \frac{33}{200}\end{array} \)
\(\begin{array}{l}(C)\ \frac{39}{200}\end{array} \)
\(\begin{array}{l}(D)\ \frac{11}{50}\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l}\left(1-x^{2}+3 x^{3}\right)\left(\frac{5}{2} x^{3}-\frac{1}{5 x^{2}}\right)^{11}, x \neq 0\end{array} \)
\(\begin{array}{l}\text{General term of}\ \left(\frac{5}{2} x^{3}-\frac{1}{5 x^{2}}\right)^{11}\ is\end{array} \)
\(\begin{array}{l}T_{r+1}={ }^{11} C_{r}\left(\frac{5}{2} x^{3}\right)^{11-r}\left(\frac{-1}{5 x^{2}}\right)^{r}\end{array} \)
\(\begin{array}{l}={ }^{11} C_{r}\left(\frac{5}{2}\right)^{11-r}\left(\frac{-1}{5}\right)^{r} x^{33-5 r}\end{array} \)
So, term independent from x in given expression
\(\begin{array}{l}=-{ }^{11} C_{7}\left(\frac{5}{2}\right)^{4}\left(\frac{-1}{5}\right)^{7}=\frac{11 \times 10 \times 9 \times 8}{24} \times \frac{1}{16 \times 125}\end{array} \)
\(\begin{array}{l}=\frac{33}{200}\end{array} \)
5. If n arithmetic means are inserted between a and 100 such that the ratio of the first mean to the last mean is 1 : 7 and a + n = 33, then the value of n is:
(A) 21
(B) 22
(C) 23
(D) 24
Answer (C)
Sol. a, A1, A2 …….. An, 100
Let d be the common difference of above A.P. then
\(\begin{array}{l}\frac{a+d}{100-d}=\frac{1}{7}\end{array} \)
⇒ 7a + 8d = 100 …(i)
and a + n = 33 …(ii)
and 100 = a + (n + 1)d
\(\begin{array}{l}\Rightarrow \quad 100=a+(34-a) \frac{(100-7 a)}{8}\end{array} \)
⇒ 800 = 8a + 7a2 – 338a + 3400
⇒ 7a2 – 330a + 2600 = 0
\(\begin{array}{l}\Rightarrow \quad a=10, \frac{260}{7}\end{array} \)
but \(\begin{array}{l}a \neq \frac{260}{7}\end{array} \)
∴ n = 23
6. Let f,g : R → R be functions defined by
\(\begin{array}{l}f(x)=\left\{\begin{array}{ll}{[x],} & x<0 \\ |1-x|, & x \geq 0\end{array}\right.$ and $g(x)= \begin{cases}e^{x}-x, & x<0 \\ (x-1)^{2}-1, & x \geq 0\end{cases}\end{array} \)
Where [x] denotes the greatest integer less than or equal to x. Then, the function fog is discontinuous at exactly :
(A) one point
(B) two points
(C) three points
(D) four points
Answer (B)
Sol.
\(\begin{array}{l}f(x)=\left\{\begin{array}{ll}{[x],} & x<0 \\ |1-x|, & x \geq 0\end{array}\right.$ and $g(x)= \begin{cases}e^{x}-x, & x<0 \\ (x-1)^{2}-1, & x \geq 0\end{cases}\end{array} \)
\(\begin{array}{l}fog(x)= \begin{cases}{[g(x)],} & g(x)<0 \\ |1-g(x)|, & g(x) \geq 0\end{cases}\end{array} \)

Graph of y = g(x)
\(\begin{array}{l}=\left\{\begin{array}{cc}\left|1+x-e^{x}\right|, & x<0 \\1, & x=0 \\{\left[(x-1)^{2}-1\right],} & 0<x<2 \\\left|2-(x-1)^{2}\right|, & x \geq 2\end{array}\right.\end{array} \)
So, x = 0, 2 are the two points where fog is discontinuous.
7. Let f : R → R be a differentiable function such that \(\begin{array}{l}f\left(\frac{\pi}{4}\right)=\sqrt{2}, f\left(\frac{\pi}{2}\right)=0 \textup{and} f^{\prime}\left(\frac{\pi}{2}\right)=1\end{array} \)
and let \(\begin{array}{l}g(x)=\int_{x}^{\frac{\pi}{4}}\left(f^{\prime}(t) \sec t+\tan t \operatorname{sec~t} f(t)\right) d t\end{array} \)
\(\begin{array}{l}\text{for}\ x \in\left[\frac{\pi}{4}, \frac{\pi}{2}\right)\ \text{Then}\ \lim _{x \rightarrow\left(\frac{\pi}{2}\right)^{-}} g(x)\ \text{is equal to}\end{array} \)
(A) 2
(B) 3
(C) 4
(D) –3
Answer (B)
Sol. Given :
\(\begin{array}{l}f\left(\frac{\pi}{4}\right)=\sqrt{2}, f\left(\frac{\pi}{2}\right)=0 \end{array} \)
and \(\begin{array}{l}f^{\prime}\left(\frac{\pi}{2}\right)=1\end{array} \)
\(\begin{array}{l}g(x)=\int_{x}^{\pi/4} \left( f'(t) sec~t +tan~t ~sec~ t f(t)\right)dt\end{array} \)
\(\begin{array}{l}=[\sec t+f(t)]_{x}^{\frac{\pi}{4}}=2-\sec x f(x)\end{array} \)
Now,
\(\begin{array}{l}\lim _{x \rightarrow \frac{\pi^{-}}{2}} g(x)=\lim _{h \rightarrow 0} g\left(\frac{\pi}{2}-h\right)=\lim _{h \rightarrow 0} 2-(\operatorname{cosec} h) f\left(\frac{\pi}{2}-h\right)\end{array} \)
\(\begin{array}{l}=\lim _{h \rightarrow 0}\left[2-\frac{f\left(\frac{\pi}{2}-h\right)}{\sin h}\right] =\lim _{h \rightarrow 0}\left[2+\frac{f^{\prime}\left(\frac{\pi}{2}-h\right)}{\cos h}\right]=3\end{array} \)
8. Let f : R → R be a continuous function satisfying f(x) + f(x + k) = n, for all x ∈ R where k > 0 and n is a positive integer. If \(\begin{array}{l}l_{1}=\int_{0}^{4 n k} f(x) d x \quad and \quad I_{2}=\int_{-k}^{3 k} f(x) d x\end{array} \)
, then
\(\begin{array}{l}(A)\ I_{1}+2 I_{2}=4 n k\end{array} \)
\(\begin{array}{l}(B)\ I_{1}+2 I_{2}=2 n k\end{array} \)
\(\begin{array}{l}(C)\ I_{1}+n I_{2}=4 n^{2} k\end{array} \)
\(\begin{array}{l}(D)\ l_{1}+n l_{2}=6 n^{2} k\end{array} \)
Answer (C)
Sol. f : R → R and f(x) + f(x + k) = n ∀ x ∈ R
x → x + k
f(x + k) + f(x + 2k) = n
∴ f(x + 2k) = f(x)
So, period of f(x) is 2k
Now,
\(\begin{array}{l} \begin{aligned}I_{1}=\int_{0}^{4 n k} f(x) d x &=2 n \int_{0}^{2 k} f(x) d x \\&=2 n\left[\int_{0}^{k} f(x) d x+\int_{k}^{2 k} f(x) d x\right]\end{aligned}\end{array} \)
x = t + k ⇒ dx = dt (in second integral)
\(\begin{array}{l}\begin{aligned}&=2 n\left[\int_{0}^{k} f(x) d x+\int_{0}^{k} f(t+k) d t\right] \\&=2 n^{2} k\end{aligned}\end{array} \)
Now,
\(\begin{array}{l}I_2=\int_{-k}^{3 k} f(x) d x=2 \int_{0}^{2 k} f(x) d x\end{array} \)
\(\begin{array}{l}I_{2}=2(n k) \end{array} \)
\(\begin{array}{l}\therefore I_{1}+n I_{2}=4 n^{2} k\end{array} \)
9. The area of the bounded region enclosed by the curve \(\begin{array}{l}y=3-\left|x-\frac{1}{2}\right|-|x+1|\end{array} \)
and the x-axis is
\(\begin{array}{l}(A)\ \frac{9}{4}\end{array} \)
\(\begin{array}{l}(B)\ \frac{45}{16}\end{array} \)
\(\begin{array}{l}(C)\ \frac{27}{8}\end{array} \)
\(\begin{array}{l}(D)\ \frac{63}{16}\end{array} \)
Answer (C)
Sol.

\(\begin{array}{l}y = \begin{aligned}& \begin{cases}2 x-\frac{7}{2} & x<-1 \\\frac{3}{2} & -1 \leq x \leq \frac{1}{2} \\\frac{5}{2}-2 x & x>\frac{1}{2}\end{cases} \\\end{aligned}\end{array} \)
\(\begin{array}{l}y = 3-\left|x-\frac{1}{2}\right|-|x+1|\end{array} \)
Area of shaded region (required area)
\(\begin{array}{l}= \frac{1}{2}\left(3+\frac{3}{2}\right) \cdot \frac{3}{2}=\frac{27}{8}\end{array} \)
10. Let x = x(y) be the solution of the differential equation \(\begin{array}{l}2 y e^{\frac{x}{y^{2}}} d x+\left(y^{2}-4 x e^{\frac{x}{y^{2}}}\right) d y=0\end{array} \)
such that x(1) = 0. Then, x(e) is equal to
(A) e loge(2)
(B) -e loge(2)
(C) e2 loge(2)
(D) -e2 loge(2)
Answer (D)
Sol. Given differential equation
\(\begin{array}{l}2 y e^{\frac{x}{y^{2}}} d x+\left(y^{2}-4 x e^{\frac{x}{y^{2}}}\right) d y=0, x(1)=0\end{array} \)
\(\begin{array}{l}\Rightarrow \quad e^{\frac{x}{y^{2}}}[2 y d x-4 x d y]=-y^{2} d y\end{array} \)
\(\begin{array}{l}\Rightarrow e^{\frac{x}{y^{2}}}\left[\frac{2 y^{2} d x-4 x y d y}{y^{4}}\right]=\frac{-1}{y} d y\end{array} \)
\(\begin{array}{l}\Rightarrow 2 e^{\frac{x}{y^{2}}} d\left(\frac{x}{y^{2}}\right)=-\frac{1}{y} d y\end{array} \)
\(\begin{array}{l}\Rightarrow 2 e^{\frac{x}{y^{2}}}=-\ln y+c…(i)\end{array} \)
Now, using x(1) = 0, c = 2
So, for x(e), Put y = e in (i)
\(\begin{array}{l}2 e^{\frac{x}{e^{2}}}=-1+2 \end{array} \)
\(\begin{array}{l}\Rightarrow \frac{x}{e^{2}}=\ln \left(\frac{1}{2}\right) \Rightarrow x(e)=-e^{2} \ln 2\end{array} \)
11. Let the slope of the tangent to a curve y = f(x) at (x, y) be given by 2 tanx(cosx – y). If the curve passes through the point (π/4, 0) then the value of \(\begin{array}{l}\int_{0}^{\pi / 2} y d x\end{array} \)
is equal to :
\(\begin{array}{l}(A)\ (2-\sqrt{2})+\frac{\pi}{\sqrt{2}}\end{array} \)
\(\begin{array}{l}(B)\ 2-\frac{\pi}{\sqrt{2}}\end{array} \)
\(\begin{array}{l}(C)\ (2+\sqrt{2})+\frac{\pi}{\sqrt{2}}\end{array} \)
\(\begin{array}{l}(D)\ 2+\frac{\pi}{\sqrt{2}}\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l}\frac{d y}{d x}=2 \tan x(\cos x-y)\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{d y}{d x}+2 \tan x y=2 \sin x\end{array} \)
\(\begin{array}{l}I.F.=e^{\int 2 \tan x d x}=\sec ^{2} x\end{array} \)
∴ Solution of D.E. will be
\(\begin{array}{l}y(x) \sec ^{2} x=\int 2 \sin x \sec ^{2} x d x\end{array} \)
\(\begin{array}{l}y \sec ^{2} x=2 \sec x+c\end{array} \)
∵ Curve passes through
\(\begin{array}{l}\left(\frac{\pi}{4}, 0\right)\end{array} \)
\(\begin{array}{l}\therefore c=-2 \sqrt{2}\end{array} \)
\(\begin{array}{l}\therefore y=2 \cos x-2 \sqrt{2} \cos ^{2} x\end{array} \)
\(\begin{array}{l}\therefore \int_{0}^{\pi / 2} y d x=\int_{0}^{\pi / 2}\left(2 \cos x-2 \sqrt{2} \cos ^{2} x\right) d x\end{array} \)
\(\begin{array}{l}=2-2 \sqrt{2} \cdot \frac{\pi}{4}=2-\frac{\pi}{\sqrt{2}}\end{array} \)
12. Let a triangle be bounded by the lines L1 : 2x + 5y = 10; L2 : –4x + 3y = 12 and the line L3, which passes through the point P(2, 3), intersects L2 at A and L1 at B. If the point P divides the line-segment AB, internally in the ratio 1 : 3, then the area of the triangle is equal to
\(\begin{array}{l}(A)\ \frac{110}{13}\end{array} \)
\(\begin{array}{l}(B)\ \frac{132}{13}\end{array} \)
\(\begin{array}{l}(C)\ \frac{142}{13}\end{array} \)
\(\begin{array}{l}(D)\ \frac{151}{13}\end{array} \)
Answer (B)
Sol. L1 : 2x + 5y = 10
L2 : – 4x + 3y = 12
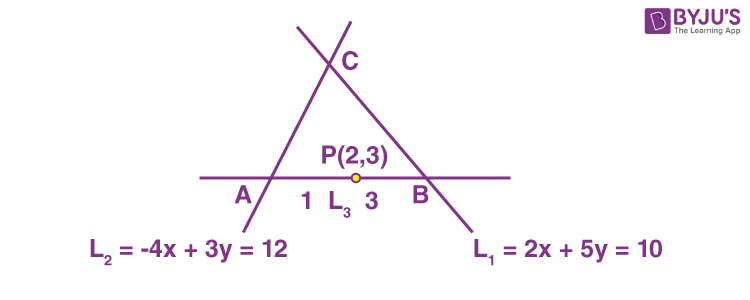
Solving L1 and L2 we get
\(\begin{array}{l}C \equiv\left(\frac{-15}{13}, \frac{32}{13}\right)\end{array} \)
Now, Let
\(\begin{array}{l}A\left(x_{1}, \frac{1}{3}\left(12+4 x_{1}\right)\right)\end{array} \)
and \(\begin{array}{l}B\left(x_{2}, \frac{1}{5}\left(10-2 x_{2}\right)\right)\end{array} \)
\(\begin{array}{l}\therefore \frac{3 x_{1}+x_{2}}{4}=2\end{array} \)
and
\(\begin{array}{l}\frac{\left(12+4 x_{1}\right)+\frac{10-2 x_{2}}{5}}{4}=3\end{array} \)
So, 3x1 + x2 = 8 and 10 x1 – x2 = – 5
So,
\(\begin{array}{l}\left(x_{1}, x_{2}\right)=\left(\frac{3}{13}, \frac{95}{13}\right)\end{array} \)
\(\begin{array}{l}A=\left(\frac{3}{13}, \frac{56}{13}\right)\end{array} \)
and \(\begin{array}{l}B=\left(\frac{95}{13}, \frac{-12}{13}\right)\end{array} \)
\(\begin{array}{l}=\left|\frac{1}{2}\left(\frac{3}{13}\left(\frac{-44}{13}\right) \frac{-56}{13}\left(\frac{110}{13}\right)+1\left(\frac{2860}{169}\right)\right)\right|\end{array} \)
\(\begin{array}{l}=\frac{132}{13} ~\text{sq. units}\end{array} \)
13. Let a > 0, b > 0. Let e and l respectively be the eccentricity and length of the latus rectum of the hyperbola \(\begin{array}{l}\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\end{array} \)
Let e′ and l′ respectively be the eccentricity and length of the latus rectum of its conjugate hyperbola. If \(\begin{array}{l}\mathrm{e}^{2}=\frac{11}{14} l\ \text{and}\ \left(\mathrm{e}^{\prime}\right)^{2}=\frac{11}{8} l^{\prime}\end{array} \)
then the value of 77a + 44b is equal to :
(A) 100
(B) 110
(C) 120
(D) 130
Answer (D)
Sol. H :
\(\begin{array}{l}\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\end{array} \)
then
\(\begin{array}{l}e^{2}=\frac{11}{14} l \quad\end{array} \)
(I be the length of LR)
\(\begin{array}{l}\Rightarrow a^{2}+b^{2}=\frac{11}{7} b^{2} a \quad \ldots(i)\end{array} \)
and
\(\begin{array}{l}e^{\prime ^2}=\frac{11}{8} l^{\prime}\end{array} \)
(I′ be the length of LR of conjugate hyperbola)
\(\begin{array}{l}\Rightarrow a^{2}+b^{2}=\frac{11}{4} a^{2} b…(ii)\end{array} \)
By (i) and (ii)
7a = 4b
then by (i)
\(\begin{array}{l}\frac{16}{49} b^{2}+b^{2}=\frac{11}{7} b^{2} \cdot \frac{4 b}{7}\end{array} \)
⇒ 44b = 65 and 77a = 65
∴ 77a + 44b = 130
14. Let, \(\begin{array}{l}\vec{a}=\alpha \hat{i}+2 \hat{j}-\hat{k}$ and $\vec{b}=-2 \hat{i}+\alpha \hat{j}+\hat{k}\end{array} \)
, where α ∈ R. If the area of the parallelogram whose adjacent sides are represented by the vectors \(\begin{array}{l}\vec{a}\ \text{and}\ \vec{b}\ is\ \sqrt{15\left(\alpha^{2}+4\right)}\ \text{, then the value of}\ 2|\vec{a}|^{2}+(\vec{a} \cdot \vec{b})|\vec{b}|^{2}\end{array} \)
is equal to :
(A) 10
(B) 7
(C) 9
(D) 14
Answer (D)
Sol.
\(\begin{array}{l}\vec{a}=\alpha \hat{i}+2 \hat{j}-\hat{k}$ and $\vec{b}=-2 \hat{i}+\alpha \hat{j}+\hat{k}\end{array} \)
\(\begin{array}{l}\therefore \vec{a} \times \vec{b}=\left|\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k} \\\alpha & 2 & -1 \\-2 & \alpha & 1\end{array}\right|=(2+\alpha) \hat{i}-(\alpha-2) \hat{j}+\left(\alpha^{2}+4\right) \hat{k}\end{array} \)
Now
\(\begin{array}{l}|\vec{a} \times \vec{b}|=\sqrt{15\left(\alpha^{2}+4\right)} \end{array} \)
⇒ (2 + α)2 + (α – 2)2 + (α2 + 4)2 = 15(α2 + 4)
⇒ α4 – 5α2 – 36 = 0
∴ α = ±3
Now,
\(\begin{array}{l}2|\vec{a}|^{2}+(\vec{a}-\vec{b})|\vec{b}|^{-2}=2.14-14=14\end{array} \)
15. If vertex of a parabola is (2, –1) and the equation of its directrix is 4x – 3y = 21, then the length of its latus rectum is :
(A) 2
(B) 8
(C) 12
(D) 16
Answer (B)
Sol. Vertex of Parabola : (2, –1)
and directrix : 4x – 3y = 21
Distance of vertex from the directrix
\(\begin{array}{l}a=\left|\frac{8+3-21}{\sqrt{25}}\right|=2\end{array} \)
∴ length of latus rectum = 4a = 8
16. Let the plane ax + by + cz = d pass through (2, 3, –5) and is perpendicular to the planes 2x + y – 5z = 10 and 3x + 5y – 7z = 12. If a, b, c, d are integers d > 0 and gcd (|a|, |b|, |c|, d) = 1, then the value of a + 7b + c + 20d is equal to :
(A) 18
(B) 20
(C) 24
(D) 22
Answer (D)
Sol. Equation of plane through point (2, 3, –5) and perpendicular to planes 2x + y – 5z = 10 and
3x + 5y – 7z = 12 is
\(\begin{array}{l}\left|\begin{array}{ccc}x-2 & y-3 & z+5 \\ 2 & 1 & -5 \\ 3 & 5 & -7\end{array}\right|=0\end{array} \)
∴ Equation of plane is (x – 2) (– 7 + 25) – (y – 3) (– 14 + 15) + (z + 5) · 7 = 0
∴ 18x – y + 7z + 2 = 0
⇒ 18x – y + 7z = – 2
∴ – 18x + y – 7z = 2
On comparing with ax + by + cz = d where d > 0 is
a = – 18, b = 1, c = – 7, d = 2
∴ a + 7b + c + 20d = 22
17. The probability that a randomly chosen one-one function from the set {a, b, c, d} to the set {1, 2, 3, 4, 5} satisfies f(a) + 2f(b) – f(c) = f(d) is :
\(\begin{array}{l}(A)\ \frac{1}{24}\end{array} \)
\(\begin{array}{l}(B)\ \frac{1}{40}\end{array} \)
\(\begin{array}{l}(C)\ \frac{1}{30}\end{array} \)
\(\begin{array}{l}(D)\ \frac{1}{20}\end{array} \)
Answer (D)
Sol. Number of one-one function from {a, b, c, d} to set {1, 2, 3, 4, 5} is
\(\begin{array}{l}{ }^{5} P_{4}=120\ n(s)\end{array} \)
The required possible set of value
(f(a), f(b), f(c), f(d)) such that f(a) + 2f(b) – f(c) = f(d) are (5, 3, 2, 1), (5, 1, 2, 3), (4, 1, 3, 5), (3, 1, 4, 5), (5, 4, 3, 2) and (3, 4, 5, 2)
∴ n(E) = 6
∴ Required probability
\(\begin{array}{l}=\frac{n(E)}{n(S)}=\frac{6}{120}=\frac{1}{20}\end{array} \)
18. The value of \(\begin{array}{l}\lim _{n \rightarrow \infty} 6 \tan \left\{\sum_{r=1}^{n} \tan ^{-1}\left(\frac{1}{r^{2}+3 r+3}\right)\right\}\end{array} \)
is equal to :
(A) 1
(B) 2
(C) 3
(D) 6
Answer (C)
Sol.
\(\begin{array}{l}\lim _{n \rightarrow \infty} 6 \tan \left\{\sum_{r=1}^{n} \tan ^{-1}\left(\frac{1}{r^{2}+3 r+3}\right)\right\}\end{array} \)
\(\begin{array}{l}=\lim _{n \rightarrow \infty} 6 \tan \left\{\sum_{r=1}^{n} \tan ^{-1}\left(\frac{(r+2)-(r+1)}{1+(r+2)(r+1)}\right)\right\}\end{array} \)
\(\begin{array}{l}=\lim _{n \rightarrow \infty} 6 \tan \left\{\sum_{r=1}^{n}\left(\tan ^{-1}(r+2)-\tan ^{-1}(r+1)\right)\right\}\end{array} \)
\(\begin{array}{l}=\lim _{n \rightarrow \infty} 6 \tan \left\{\tan ^{-1}(n+2)-\tan ^{-1} 2\right\}\end{array} \)
\(\begin{array}{l}=6 \tan \left\{\frac{\pi}{2}-\cot ^{-1}\left(\frac{1}{2}\right)\right\}\end{array} \)
\(\begin{array}{l}=6 \tan \left(\tan ^{-1}\left(\frac{1}{2}\right)\right) = 3\end{array} \)
19. Let \(\begin{array}{l}\vec{a}\ \text{be a vector which is perpendicular to the vector}\end{array} \)
\(\begin{array}{l}3 \hat{i}+\frac{1}{2} \hat{j}+2 \hat{k}.\ \text{If }\ \vec{a} \times(2 \hat{i}+\hat{k})=2 \hat{i}-13 \hat{j}-4 \hat{k}\end{array} \)
, then the projection of the vector on the vector \(\begin{array}{l}2 \hat{i}+2 \hat{j}+\hat{k}\ \text{is}:\end{array} \)
(A) 1/3
(B) 1
(C) 5/3
(D) 7/3
Answer (C)
Sol. Let
\(\begin{array}{l}\vec{a}=a_{1} \hat{i}+a_{2} \hat{j}+a_{3} \hat{k}\end{array} \)
and
\(\begin{array}{l}\vec{a} \cdot\left(3 \hat{i}-\frac{1}{2} \hat{j}+2 \hat{k}\right)=0 \Rightarrow 3 a_{1}+\frac{a_{2}}{2}+2 a_{3}=0…(i)\end{array} \)
and
\(\begin{array}{l}\vec{a} \times(2 \hat{i}+\hat{k})=2 \hat{i}-13 \hat{j}-4 \hat{k}\end{array} \)
\(\begin{array}{l}\Rightarrow a_{2} \hat{i}+\left(2 a_{3}-a_{1}\right) \hat{j}-2 a_{2} \hat{k}=2 \hat{i}-13 \hat{j}-4 \hat{k}\end{array} \)
∴ a2 = 2 …(ii)
and a1 – 2a3 = 13 …(iii)
From eq. (i) and (iii) : a1 = 3 and a3 = –5
\(\begin{array}{l}\therefore \vec{a}=3 \hat{i}+2 \hat{j}-5 \hat{k}\end{array} \)
\(\begin{array}{l}\therefore \text{projection of}\ \vec{a}\ on\ 2 \hat{i}+2 \hat{j}+\hat{k}=\frac{6+4-5}{3}=\frac{5}{3}\end{array} \)
20. If \(\begin{array}{l}cot~\alpha = 1\ \text{and}\ sec ~\beta = -\frac{5}{3}\ \text{where}\ \pi<\alpha<\frac{3\pi}{2}\ \text{and}\ \frac{\pi}{2}<\beta<\pi,\end{array} \)
then the value of tan(α + β) and the quadrant in which α + β lies, respectively are :
(A) -1/7 and IVth quadrant
(B) 7 and Ist quadrant
(C) – 7 and IVth quadrant
(D) 1/7 and Ist quadrant
Answer (A)
Sol. ∵ cot α = 1,
\(\begin{array}{l}\alpha \in\left(\pi, \frac{3 \pi}{2}\right)\end{array} \)
then tan α = 1
and
\(\begin{array}{l}\sec \beta=-\frac{5}{3}, \quad \beta \in\left(\frac{\pi}{2}, \pi\right)\end{array} \)
then
\(\begin{array}{l}\tan \beta=-\frac{4}{3}\end{array} \)
\(\begin{array}{l}\therefore \quad \tan (\alpha+\beta)=\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \cdot \tan \beta}\end{array} \)
\(\begin{array}{l}=\frac{1-\frac{4}{3}}{1+\frac{4}{3}}\end{array} \)
\(\begin{array}{l}=-\frac{1}{7}\end{array} \)
\(\begin{array}{l}\alpha+\beta \in\left(\frac{3 \pi}{2}, 2 \pi\right)\end{array} \)
i.e. fourth quadrant
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, –00.33, –00.30, 30.27, –27.30) using the mouse and the on-screen virtual numeric keypad in the place designated to enter the answer.
1. Let the image of the point P(1, 2, 3) in the line \(\begin{array}{l}L: \frac{x-6}{3}=\frac{y-1}{2}=\frac{z-2}{3}\end{array} \)
be Q. Let R (α, β, γ) be a point that divides internally the line segment PQ in the ratio 1 : 3. Then the value of 22(α + β + γ) is equal to ________.
Answer (125)
Sol. The point dividing PQ in the ratio 1 : 3 will be mid-point of P & foot of perpendicular from P on the line.
∴ Let a point on line be λ
\(\begin{array}{l}\Rightarrow \frac{x-6}{3}=\frac{y-1}{2}=\frac{z-2}{3}=\lambda\end{array} \)
\(\begin{array}{l}\Rightarrow P^{\prime}(3 \lambda+6,2 \lambda+1,3 \lambda+2)\end{array} \)
as P′ is foot of perpendicular
(3λ + 5)3 + (2λ – 1)2 + (3λ – 1)3 = 0
⇒ 22λ + 15 – 2 – 3 = 0
\(\begin{array}{l}\Rightarrow \lambda = \frac{-5}{11}\end{array} \)
\(\begin{array}{l}\therefore P’ \left ( \frac{51}{11}, \frac{1}{11},\frac{7}{11} \right )\end{array} \)
Mid-point of PP’
\(\begin{array}{l} \equiv\left(\frac{\frac{51}{11}+1}{2}, \frac{\frac{1}{11}+2}{2}, \frac{\frac{7}{11}+3}{2}\right)\equiv\left(\frac{62}{22}, \frac{23}{22}, \frac{40}{22}\right) \equiv(\alpha, \beta, \gamma)\end{array} \)
⇒ 22(α + β + γ) = 62 + 23 + 40 = 125
2. Suppose a class has 7 students. The average marks of these students in the mathematics examination is 62, and their variance is 20. A student fails in the examination if he/she gets less than 50 marks, then in worst case, the number of students can fail is __________.
Answer (0)
Sol. According to given data
\(\begin{array}{l}\frac{\displaystyle \sum \limits_{i=1}^{7}(x_i-62)^2}{7} =20 \end{array} \)
\(\begin{array}{l}\Rightarrow \sum_{i=1}^{7}\left(x_{i}-62\right)^{2}=140\end{array} \)
So for any xi , (xi – 62)2 ≤ 140
⇒ xi > 50 ∀ i = 1, 2, 3, …7
So no student is going to score less than 50.
3. If one of the diameters of the circle \(\begin{array}{l}x^{2}+y^{2}-2 \sqrt{2} x-6 \sqrt{2} y+14=0\end{array} \)
is a chord of the circle \(\begin{array}{l}(x-2 \sqrt{2})^{2}+(y-2 \sqrt{2})^{2}=r^{2}\end{array} \)
, then the value of r2 is equal to _______.
Answer (10)
Sol. For
\(\begin{array}{l}x^{2}+y^{2}-2 \sqrt{2} x-6 \sqrt{2} y+14=0\end{array} \)
Radius
\(\begin{array}{l}=\sqrt{(\sqrt{2})^{2}+(3 \sqrt{2})^{2}-14}=\sqrt{6}\end{array} \)
⇒ Diameter = 2√6
If this diameter is chord to
\(\begin{array}{l}(x-2 \sqrt{2})^{2}+(y-2 \sqrt{2})^{2}=r^{2}\end{array} \)
then
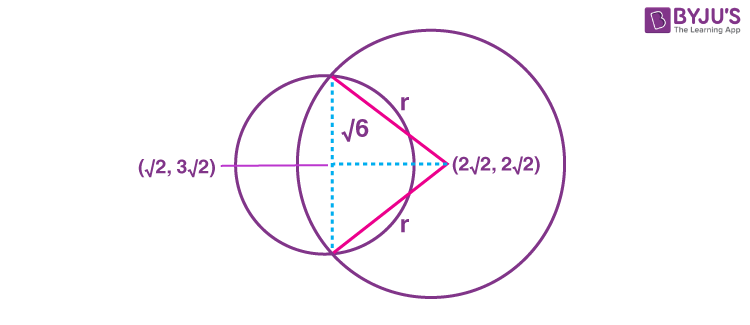
\(\begin{array}{l}\Rightarrow r^{2}=6+\left(\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}\right)^{2}\end{array} \)
⇒ r2 = 6 + 4 = 10
⇒ r2 = 10
4. If \(\begin{array}{l}\lim _{x \rightarrow 1} \frac{\sin \left(3 x^{2}-4 x+1\right)-x^{2}+1}{2 x^{3}-7 x^{2}+a x+b}=-2\end{array} \)
, then the value of (a – b) is equal to _______.
Answer (11)
Sol.
\(\begin{array}{l}\lim _{x \rightarrow 1} \frac{\left(\frac{\sin \left(3 x^{2}-4 x+1\right)}{3 x^{2}-4 x+1}\right)\left(3 x^{2}-4 x+1\right)-x^{2}+1}{2 x^{3}-7 x^{2}+a x+b}=-2\end{array} \)
\(\begin{array}{l}\Rightarrow \lim _{x \rightarrow 1} \frac{3 x^{2}-4 x+1-x^{2}+1}{2 x^{3}-7 x^{2}+a x+b}=-2\end{array} \)
\(\begin{array}{l}\Rightarrow \lim _{x \rightarrow 1} \frac{2(x-1)^{2}}{2 x^{3}-7 x^{2}+a x+b}=-2\end{array} \)
So f(x) = 2x3 – 7x2 + ax +b = 0 has x = 1 as repeated root, therefore f(1) = 0 and f ′(1) = 0 gives
a + b + 5 and a = 8
So, a – b = 11
5. Let for n = 1, 2, …, 50, Sn be the sum of the infinite geometric progression whose first term is n2 and whose common ratio is \(\begin{array}{l}\frac{1}{(n+1)^{2}}\ \text{. Then the value of}\end{array} \)
\(\begin{array}{l}\frac{1}{26}+\sum_{n=1}^{50}\left(S_{n}+\frac{2}{n+1}-n-1\right)\end{array} \)
is equal to ________.
Answer (41651)
Sol.
\(\begin{array}{l}S_{n}=\frac{n^{2}}{1-\frac{1}{(n+1)^{2}}}=\frac{n(n+1)^{2}}{n+2}=\left(n^{2}+1\right)-\frac{2}{n+2}\end{array} \)
Now
\(\begin{array}{l}\frac{1}{26}+\sum_{n=1}^{50}\left(S_{n}+\frac{2}{n+1}-n-1\right)\end{array} \)
\(\begin{array}{l}=\frac{1}{26}+\sum_{n=1}^{50}\left\{\left(n^{2}-n\right)+2\left(\frac{1}{n+1}-\frac{1}{n+2}\right)\right\}\end{array} \)
\(\begin{array}{l}=\frac{1}{26}+\frac{50 \times 51 \times 101}{6}-\frac{50 \times 51}{2}+2\left(\frac{1}{2}-\frac{1}{52}\right)\end{array} \)
= 1 + 25 × 17 (101 – 3)
= 41651
6. If the system of linear equations
2x – 3y = γ + 5,
αx + 5y = β + 1, where α, β, γ ∈ R has infinitely many solutions, then the value of |9α + 3β + 5γ| is equal to _______.
Answer (58)
Sol. If 2x – 3y = γ + 5 and αx + 5y = β + 1 have infinitely many solutions then
\(\begin{array}{l}\frac{2}{\alpha}=\frac{-3}{5}=\frac{\gamma+5}{\beta+1}\end{array} \)
\(\begin{array}{l}\Rightarrow \alpha=-\frac{10}{3}\end{array} \)
and 3β + 5γ = –28
So |9α + 3β + 5γ| = |–30 – 28| = 58
7. Let \(\begin{array}{l}A=\left(\begin{array}{cc}1+i & 1 \\ -i & 0\end{array}\right)\ \text{where}\ i=\sqrt{-1}.\end{array} \)
Then, the number of elements in the set \(\begin{array}{l}\left\{n \in\{1,2, \ldots, 100\}: A^{n}=A\right\}\end{array} \)
is ________.
Answer (25)
Sol.
\(\begin{array}{l}\therefore A^{2}=\left[\begin{array}{cc}1+i & 1 \\ -i & 0\end{array}\right]\left[\begin{array}{cc}1+i & 1 \\ -1 & 0\end{array}\right]=\left[\begin{array}{cc}i & 1+i \\ 1-i & -i\end{array}\right]\end{array} \)
\(\begin{array}{l}A^{4}=\left[\begin{array}{cc}i & 1+i \\ 1-i & -i\end{array}\right]\left[\begin{array}{cc}i & 1+i \\ 1-i & -i\end{array}\right]=l\end{array} \)
So A5 = A, A9 = A and so on.
Clearly n = 1, 5, 9, ….., 97
Number of values of n = 25
8. Sum of squares of modulus of all the complex numbers z satisfying \(\begin{array}{l}\bar{z}=iz^2 + z^2 – z\end{array} \)
is equal to ________.
Answer (2)
Sol. Let z = x + iy
So 2x = (1 + i)(x2 – y2 + 2xyi)
⇒ 2x = x2 – y2 – 2xy …(i) and
x2 – y2 + 2xy = 0 …(ii)
From (i) and (ii) we get
x = 0 or
\(\begin{array}{l}y = -\frac{1}{2}\end{array} \)
When x = 0 we get y = 0
When
\(\begin{array}{l}y = -\frac{1}{2}\end{array} \)
we get \(\begin{array}{l}x^{2}-x-\frac{1}{4}=0\end{array} \)
\(\begin{array}{l}\Rightarrow x=\frac{-1 \pm \sqrt{2}}{2}\end{array} \)
So there will be total 3 possible values of z, which are
\(\begin{array}{l}0,\left(\frac{-1+\sqrt{2}}{2}\right)-\frac{1}{2} i~ \text{and} \left(\frac{-1-\sqrt{2}}{2}\right)-\frac{1}{2}i\end{array} \)
Sum of squares of modulus
\(\begin{array}{l}=0+\left(\frac{\sqrt{2}-1}{2}\right)^{2}+\frac{1}{4}+\left(\frac{\sqrt{2}+1}{2}\right)^{2}=+\frac{1}{4}\end{array} \)
= 2
9. Let S = {1, 2, 3, 4}. Then the number of elements in the set {f : S × S → S : f is onto and f(a,b)=f(b,a) ≥ a ∀ (a, b)∈ S × S is _____.
Answer (37)
Sol. There are 16 ordered pairs in S × S. We write all these ordered pairs in 4 sets as follows.
A = {(1, 1)}
B = {(1, 4), (2, 4), (3, 4) (4, 4), (4, 3), (4, 2), (4, 1)}
C = {(1, 3), (2, 3), (3, 3), (3, 2), (3, 1)}
D = {(1, 2), (2, 2), (2, 1)}
All elements of set B have image 4 and only element of A has image 1.
All elements of set C have image 3 or 4 and all elements of set D have image 2 or 3 or 4.
We will solve this question in two cases.
Case I : When no element of set C has image 3.
Number of onto functions = 2 (when elements of set D have images 2 or 3)
Case II : When atleast one element of set C has image 3.
Number of onto functions = (23 – 1)(1 + 2 + 2)
= 35
Total number of functions = 37
10. The maximum number of compound propositions, out of p ∨ r ∨ s, p ∨ r ∨ ~s, p ∨ ~q ∨ s, ~p ∨ ~r ∨ s, ~p ∨ ~r ∨ ~s, ~p ∨ q ∨ ~s, q ∨ r ∨ ~s, q ∨ ~r ∨ ~s, ~p ∨ ~q ∨ ~s that can be made simultaneously true by an assignment of the truth values to p, q, r and s, is equal to ____________ .
Answer (9)
Sol. There are total 9 compound propositions, out of which 6 contain ~s. So if we assign s as false, these 6 propositions will be true.
In remaining 3 compound propositions, two contain p and the third contains ~r. So if we assign p and r as true and false respectively, these 3 propositions will also be true.
Hence maximum number of propositions that can be true are 9.
JEE Main 2022 Question Paper June 28th Shift 2 – Video Solutions
JEE Main 2022 June 28 Shift 2 Question Paper – Physics Solutions
JEE Main 2022 June 28 Shift 2 Question Paper – Chemistry Solutions
JEE Main 2022 June 28 Shift 2 Question Paper – Maths Solutions
Frequently Asked Questions – FAQs
Q1
How was the JEE Main 2022 June 28 Shift 2 Maths question paper?
JEE Main 2022 June 28 Shift 2 Maths question paper was of moderate difficulty. It had 7 easy questions, 12 medium questions and 4 difficult questions as per the memory-based question paper.
Q2
How many marks will be reduced for an incorrect answer in section A of JEE Main 2022 Shift 2 June 28 Maths question paper?
1 mark will be reduced for every incorrect answer in section A of JEE Main 2022 Shift 2 June 28 Maths question paper.
Q3
What is the overall difficulty level of the JEE Main 2022 June 28 Maths Shift 2 question paper?
The overall difficulty level of the JEE Main 2022 June 28 Maths Shift 2 question paper is 1.87 out of 3.
Q4
How was the class-wise distribution of questions in the JEE Main 2022 Shift 2 June 28 Maths question paper?
There were 13 questions from Class 11 and 10 questions from Class 12 in the JEE Main 2022 Shift 2 June 28 Maths question paper as per the memory-based question paper.
Q5
What is the difficulty level of questions asked from Vector algebra in the JEE Main 2022 Maths Shift 2 June 28 question paper?
The questions asked from Vector algebra in the JEE Main 2022 Maths Shift 2 June 28 question paper were easy.
















Comments