Hyperbola

Hyperbola is defined as an open curve having two branches which are mirror images of each other. It is two curves that are like infinite bows. Here, we will study the hyperbola equation, foci, eccentricity, directrix, latus rectum and characteristics of such curves.

Download this lesson as PDF:-Hyperbola PDF

What Is Hyperbola?

A hyperbola is a locus of points in such a way that the distance to each focus is a constant greater than one. In other words, the locus of a point moving in a plane in such a way that the ratio of its distance from a fixed point (focus) to that from a fixed line (directrix) is a constant greater than 1.

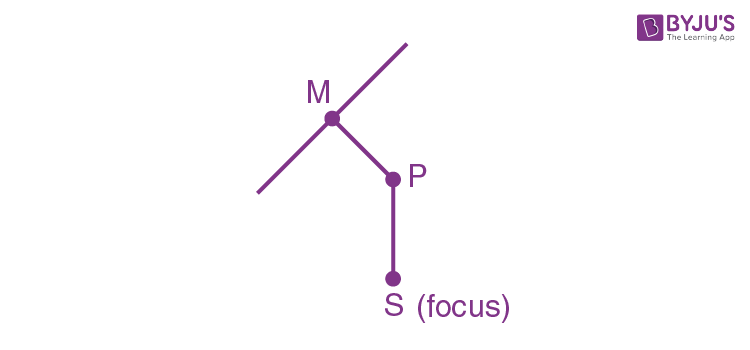
[Note: The point (focus) does not lie on the line (directrix)]

(PS/PM) = e > 1 (eccentricity)

Standard Equation of Hyperbola

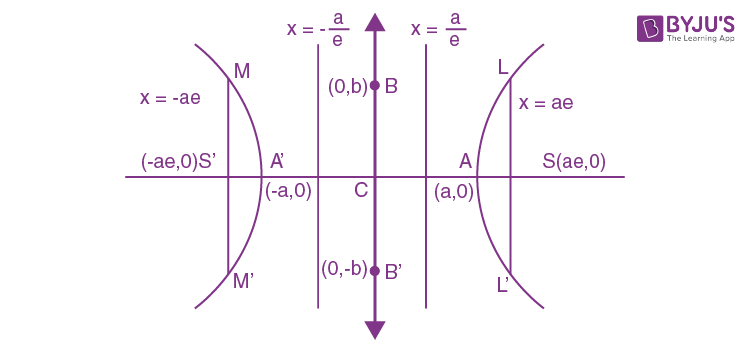
The equation of the hyperbola is simplest when the centre of the hyperbola is at the origin, and the foci are either on the x-axis or on the y-axis.  The standard equation of a hyperbola is given as follows:

[(x² / a²) – (y² / b²)] = 1

where , b² = a² (e²  – 1)

Important Terms and Formulas of Hyperbola

There are certain terms related to a hyperbola which need to be thoroughly understood to be able to get confident with this concept. Some of the most important terms related to hyperbola are:

• Eccentricity (e): e² = 1 + (b² / a²) = 1 + [(conjugate axis)² / (transverse axis)²]
• Focii: S = (ae, 0) & S′ = (−ae, 0)
• Directrix: x=(a/e), x = (−a / e)
• Transverse axis:

The live segment A’A of length 2a in which the foci S’ and S both lie is called the transverse axis of the hyperbola.

• Conjugate axis:

The line segment B’B of length 2b between the 2 points B’ = (0, -b) & B = (0, b) is called the conjugate axis of the hyperbola.

• Principal axes:

The transverse axis and conjugate axis.

• Vertices:

A = (a, 0) & A’ = (-a, 0)

• Focal chord:

A chord which passes through a focus is called a focal chord.

• Double ordinate:

The chord perpendicular to the transverse axis is called a double ordinate.

• Latus rectum:

The focal chord ⊥^r to the transverse axis is called the latus rectum.

Its length = (2b² / a) = [(conjugate)² / transverse] = 2a (e² − 1)

The difference in focal distances is a constant

i.e., |PS−PS′| = 2a

Length of latus rectum = 2 e × (distance of focus from the corresponding directrix)

End points of L.R: (± ae, ± b² / a)

Centre:

The point which bisects every chord of the conic, drawn through it, is called the centre of the conic.

C: (0, 0) is the centre of [(x² / a²) – (y² / b²)] = 1

Note:

You will notice that the results for an ellipse are also applicable for a hyperbola. You need to replace b² by (−b²)

Recommended Video

Practice Problems on Hyperbola

Example 1:

Find the equation of the hyperbola whose directrix is 2x + y = 1, focus (1, 2) and eccentricity √3.

Solution:

Let P(x, y) be any point on the hyperbola.

Draw PM perpendicular from P on the directrix,

Then, by definition SP = ePM.

⇒ (SP)² = e² (PM)²

⇒ (x − 1)² + (y − 2)² = 3{(2x + y – 1) / √(4+1)}²

⇒ 5 (x² + y² − 2x − 4y + 5)

= 3 (4x² + y² + 1 + 4xy − 2y − 4x)

⇒ 7x² − 2y² + 12xy − 2x + 14y – 22 = 0

Which is the required hyperbola.

Example 2:

Find the eccentricity of the hyperbola whose latus rectum is half of its transverse axis.

Solution:

Let the equation of hyperbola be [(x² / a²) – (y² / b²)] = 1

Then transverse axis = 2a and latus – rectum = (2b² / a)

According to question (2b² / a) = (1/2) × 2a

⇒ 2b² = a² (Since, b² = a² (e² − 1))

⇒ 2a² (e² − 1) = a²

⇒ 2e² – 2 = 1

⇒ e² = (3 / 2)

∴ e = √(3/2)

Hence, the required eccentricity is √(3/2)

What Is Conjugate Hyperbola?

2 hyperbolas such that the transverse and conjugate axes of one hyperbola are respectively the conjugate and transverse axis of the other are called conjugate hyperbola of each other.

(x² / a²) – (y² /b²) = 1 & (−x² / a²) + (y² / b²) = 1 are conjugate hyperbolas of each other.

(y² / b²) – (x² / a²) = 1

a² = b² (e² − 1)

Vertices: Vertices: (0,±b) and L.R. = (2a² / b)

Some Important Conclusions on Conjugate Hyperbola

(a) If e1 and e2 are eccentricities of the hyperbola and its conjugate, then

(1 / e₁²) + (1 / e₂²) = 1

(b) The foci of a hyperbola and its conjugate are concyclic and form the vertices of a square.

(c) 2 hyperbolas are similar if they have the same eccentricities.

(d) 2 similar hyperbolas are equal if they have the same latus rectum.

Example 3:

Find the lengths of the transverse axis and conjugate axis, eccentricity, the co-ordinates of foci, vertices, length of the latus-rectum and equations of the directrices of the hyperbola, 16x² − 9y² = −144.

Solution:

The equation 16x² − 9y² = −144 can be written as (x² / 9) – (y² / 16) = −1

This is of the form (x² / a²) – (y² / b²) = −1

∴ a² = 9, b² = 16

⇒ a=3, b=4

Length of transverse axis: The length of transverse axis = 2b = 8

Length of conjugate axis: The length of conjugate axis = 2a = 6

Eccentricity:

Foci: The co-ordinates of the foci are (0, ± be), i.e., (0, ± 5)

Vertices: The co-ordinates of the vertices are (0, ± b), i.e., (0, ± 4)

Lengths of latus-rectum: The length of latus-rectum = (2a² / b) = [2(3)²] / 4 = 9/2

Equation of directrices: The equation of directrices are

y = ± (b/e) ⇒y = ± [4 / (5/4)] ⇒ y ± (16 / 5)

Auxiliary Circles of the Hyperbola

A circle is drawn with centre C and transverse axis as the diameter is called the auxiliary circle of the hyperbola. The auxiliary circle of the hyperbola equation is given as:

The equation of the auxiliary circle is x² + y² = a²,

Note from the following figure that P and Q are called the “corresponding points” of the hyperbola and the auxiliary circle.

Parametric Representation:

x = a sec θ and y = b tan θ

i.e., if (a sec θ, b tan θ) is on the hyperbola, then Q: (a cos θ, a sin θ) lies on the auxiliary circle. The equation of chord joining 2 points P (α) and Q (f) is given by:

The position of a point P

S₁ = x₁²/a² + y²/b² = 1 is positive, zero or negative accordingly as (x₁, y₁) lies inside, on or outside is positive, and zero or negative accordingly as (x₁, y₁) lies inside, on or outside.

Example 4: Find the position of the point (5, -4) relative to the hyperbola 9x² – y² = 1.

Solution:

Since 9(5)² – (-4)² – 1 = 225 – 16 – 1 = 208 > 0,

So, the point (5, -4) lies inside the hyperbola 9x² – y² = 1.

Rectangular Hyperbola

A rectangular hyperbola for which hyperbola axes (or asymptotes) are perpendicular or with an eccentricity is √2. Hyperbola with conjugate axis = transverse axis is a = b, which is an example of a rectangular hyperbola.

x²/a² – y²/b²

⇒ x²/a² – y²/a² = 1

Or, x² – y² = a²

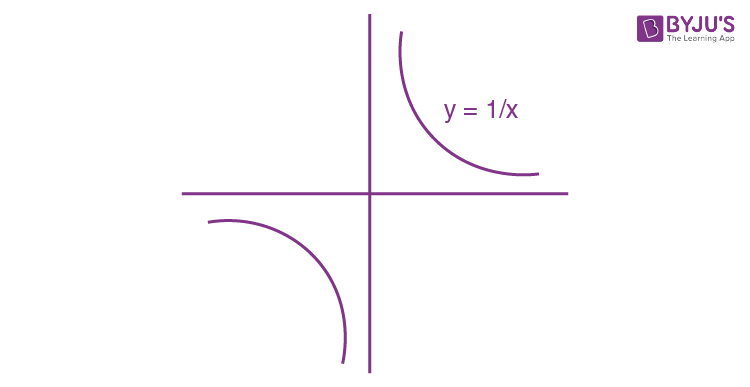
The eccentricity of a rectangular hyperbola

Also, xy = c

e.g. xy = 1, y = 1/x

Tangent of Rectangular Hyperbola

The tangent of a rectangular hyperbola is a line that touches a point on the rectangular hyperbola’s curve. The equation and slope form of a rectangular hyperbola’s tangent is given as:

Equation of tangent

The y = mx + c write hyperbola x²/a² – y²/b² = 1 will be tangent if c² = a²/m² – b².

Slope form of tangent

y = mx ± √(a²m² – b²)

Secant

Secant will cut ellipse at 2 distinct points

⇒ c² > a² m² – b²

Neither secant nor tangent

For the line to be neither secant nor tangent, a quadratic equation will give an imaginary solution.

⇒ c² < a² m² – b²

Equation of tangent to hyperbola x² /a² – y²/b² = 1 at point (x₁ ,y₁) is

(xx₁)/a₂ = (yy₁)/b₁ = 1

Parametric form of tangent:

(x secθ) /a − (y tanθ)/b = 1

Point of contact and examples on tangent

Compare:

y = mx + c

(xx₁)/a² – (yy₁)/b² = 1 – mx + y = c

x₁ = (-a²c)/m;

y₁ = -b²/c

(x₁,y₁) = [(-a²m)/c, -b²/c]

Solved Examples on Hyperbola

Example 5: Find the equation of a tangent to hyperbola x²/9−y²=1 whose slope is 5.

Solution:

Slope of tangent m = 5, a² = 9, b² = 1

The equation of tangent in slope form is

y = mx ± √(a²m² – b² )

y = 5x ± √(9.5² – 1)

y = 5x ± 4√14

[Note: For ellipse, director circle is x² + y² = a² + b², x²/a² + y²/b² = 1]

Normal:

Equation of normal of x²/a² – y²/b² = 1 at (x₁ ,y₁)

a²x/x₁ + b²y/y₁ = a² + b²

Example 6: Find normal at the point (6, 3) to hyperbola x²/18 − y²/9 = 1.

Solution:

Equation of normal at point (x₁, y₁) is a² = 18, b² = 9

a²x/x₁ + b²y/y₁ = a² + b²

The equation of normal at point (6, 3) is

18x/6 + 9y/3 = 18 + 9

x + y = 9

Example 7: Find the equation of the chord of contact of point (2, 3) to hyperbola x²/16 − y²/9 = 1.

Solution:

The equation of the chord of contact is T = 0

i.e. (xx₁)/a² – (yy₁)/b² – 1 = 0

Or, 2x/16 – 3y/9 = 1

Or, x/8 – y/3 = 1

Equation of chord when mid-point is given

T = (xx₁)/a² – (yy₁)/b² – 1 = x₁²/a² – y₁²/b² − 1.

Example 9: Find the equation of chord of hyperbola x²/9 – y²/4 = 1 whose midpoint is (5, 1).

Solution:

We know that equation of the chord of the hyperbola whose midpoints is (x₁, y₁)

T = (xx₁)/a² – (yy₁)/b² – 1 = x₁²/a² – y₁²/b² − 1

Given, the midpoint is (5, 1).

=>5x/9 – y/4 – 1= 25/9 – ¼ – 1

=>5x/9 – y/4 = 91/36

Hyperbola Short Notes and Revision

Ellipse and Hyperbola Important JEE Main Questions

Hyperbola – Top 12 Most Important and Expected JEE Main Questions

Ellipse and Hyperbola – Important Topics

Ellipse and Hyperbola – Important Questions