Inverse trigonometric functions are defined as the inverse functions of the basic trigonometric functions, which are sine, cosine, tangent, cotangent, secant and cosecant functions. They are also termed arcus functions, antitrigonometric functions or cyclometric functions. These inverse functions in trigonometry are used to get the angle with any of the trigonometry ratios. The inverse trigonometry functions have major applications in the field of engineering, physics, geometry and navigation.
Table of Contents
What Are Inverse Trigonometric Functions?
Inverse trigonometric functions are also called “arc functions” since, for a given value of trigonometric functions, they produce the length of arc needed to obtain that particular value. The inverse trigonometric functions perform the opposite operation of the trigonometric functions such as sine, cosine, tangent, cosecant, secant and cotangent. We know that trigonometric functions are applicable, especially to the right-angle triangle. These six important functions are used to find the angle measure in the right-angle triangle when two sides of the triangle measures are known.
Formulas
The basic inverse trigonometric formulas are as follows:
| Inverse Trig Functions | Formulas |
| Arcsine | sin-1(-x) = -sin-1(x), x ∈ [-1, 1] |
| Arccosine | cos-1(-x) = π -cos-1(x), x ∈ [-1, 1] |
| Arctangent | tan-1(-x) = -tan-1(x), x ∈ R |
| Arccotangent | cot-1(-x) = π – cot-1(x), x ∈ R |
| Arcsecant | sec-1(-x) = π -sec-1(x), |x| ≥ 1 |
| Arccosecant | cosec-1(-x) = -cosec-1(x), |x| ≥ 1 |
Inverse Trigonometric Functions Graphs
There are particularly six inverse trig functions for each trigonometry ratio. The inverse of six important trigonometric functions are
- Arcsine
- Arccosine
- Arctangent
- Arccotangent
- Arcsecant
- Arccosecant
Let us discuss all six important types of inverse trigonometric functions, along with its definition, formulas, graphs, properties and solved examples.
Arcsine Function
The arcsine function is an inverse of the sine function denoted by sin-1x. It is represented in the graph as shown below.
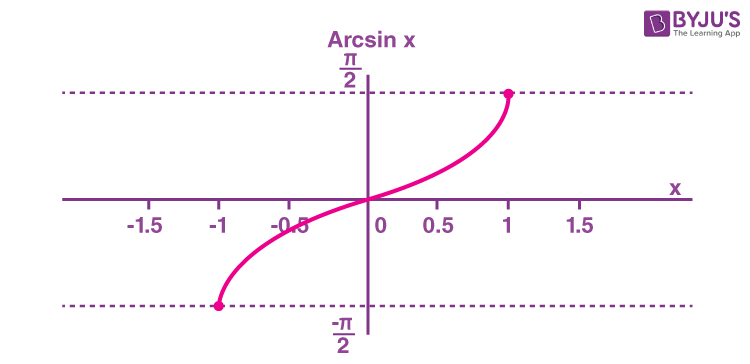
| Domain | -1 ≤ x ≤ 1 |
| Range | -π/2 ≤ y ≤ π/2 |
Arccosine Function
The arccosine function is the inverse of the cosine function denoted by cos-1x. It is represented in the graph as shown below.
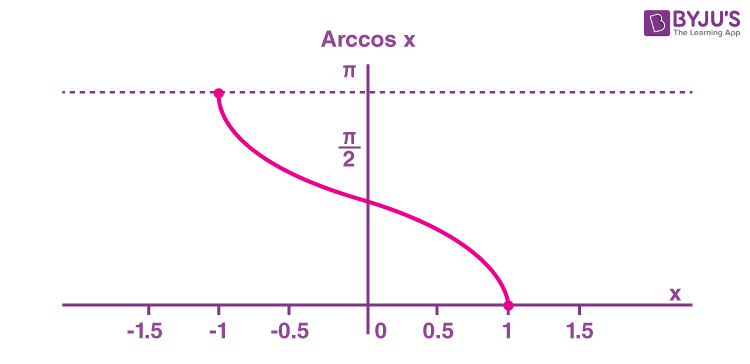
Therefore, the inverse of the cos function can be expressed as y = cos-1x (arccosine x)
Domain and range of arcsine function are as follows:
| Domain | -1≤x≤1 |
| Range | 0 ≤ y ≤ π |
Arctangent Function
The arctangent function is the inverse of the tangent function denoted by tan-1x. It is represented in the graph as shown below.
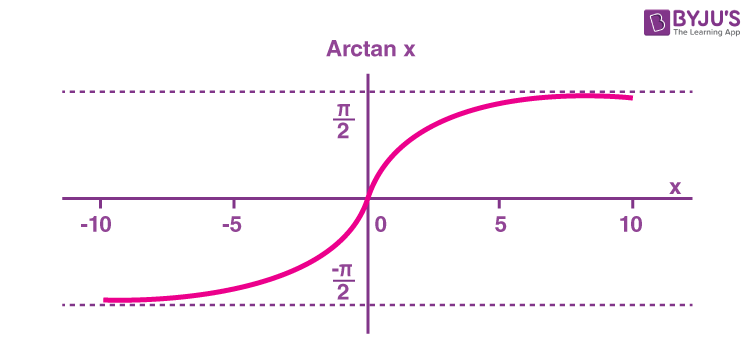
Therefore, the inverse of the tangent function can be expressed as y = tan-1x (arctangent x)
Domain and range of arctangent are as follows:
| Domain | -∞ < x < ∞ |
| Range | -π/2 < y < π/2 |
Arccotangent (Arccot) Function
The arccotangent function is the inverse of the cotangent function denoted by cot-1x.
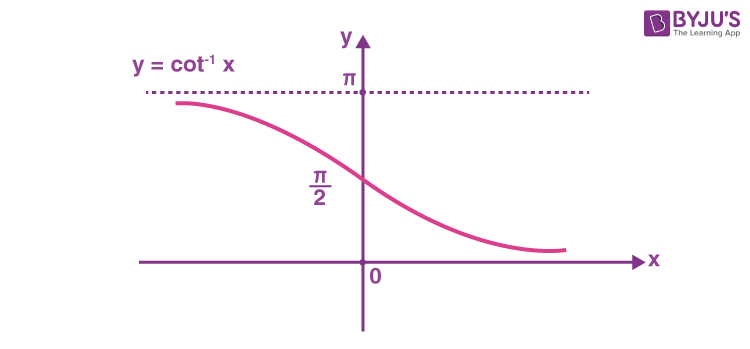
Therefore, the inverse of the cotangent function can be expressed as y = cot-1x (arccotangent x)
Domain and range of arccotangent are as follows:
| Domain | -∞ < x < ∞ |
| Range | 0 < y < π |
Arcsecant Function
What is the arcsecant (arcsec) function? The arcsecant function is the inverse of the secant function denoted by sec-1x. It is represented in the graph as shown below.
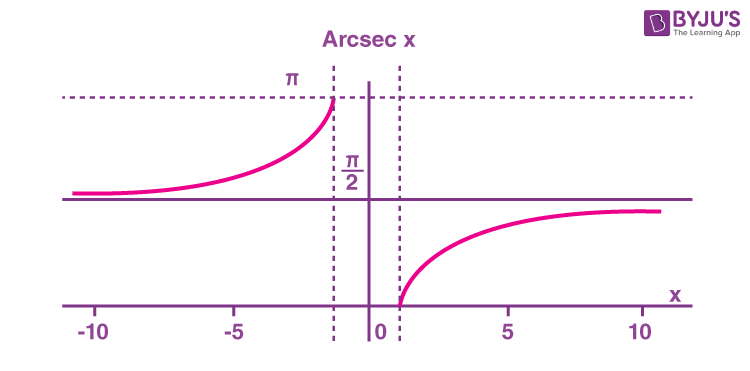
Therefore, the inverse of the secant function can be expressed as y = sec-1x (arcsecant x)
Domain and range of arcsecant are as follows:
| Domain | -∞ ≤ x ≤ -1 or 1 ≤ x ≤ ∞ |
| Range | 0 ≤ y ≤ π, y ≠ π/2 |
Arccosecant Function
What is the arccosecant (arccsc x) function? The arccosecant function is the inverse of the cosecant function denoted by cosec-1x. It is represented in the graph as shown below.
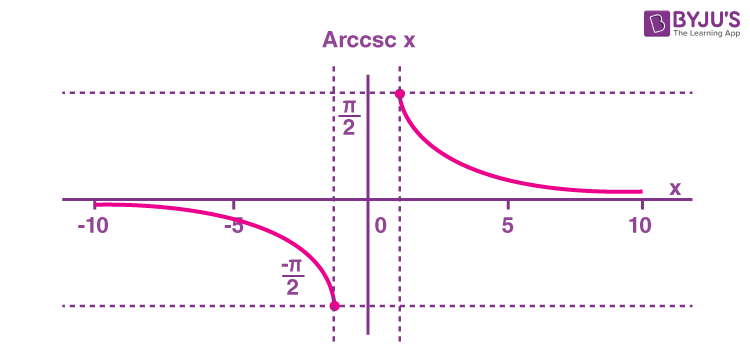
Therefore, the inverse of the cosecant function can be expressed as y = cosec-1x (arccosecant x)
Domain and range of arccosecant are:
| Domain | -∞ ≤ x ≤ -1 or 1 ≤ x ≤ ∞ |
| Range | -π/2 ≤ y ≤ π/2, y ≠ 0 |
Inverse Trigonometric Functions Table
Let us look at all the inverse trigonometric functions with their notation, definition, domain and range.
| Function Name | Notation | Definition | Domain of x | Range |
| Arcsine or inverse sine | y = sin-1(x) | x=sin y | −1 ≤ x ≤ 1 |
|
| Arccosine or inverse cosine | y=cos-1(x) | x=cos y | −1 ≤ x ≤ 1 |
|
| Arctangent or
inverse tangent |
y=tan-1(x) | x=tan y | For all real numbers |
|
| Arccotangent or
inverse cot |
y=cot-1(x) | x=cot y | For all real numbers |
|
| Arcsecant or
inverse secant |
y = sec-1(x) | x=sec y | x ≤ −1 or 1 ≤ x |
|
| Arccosecant | y=csc-1(x) | x=csc y | x ≤ −1 or 1 ≤ x |
|
Inverse Trigonometric Functions Derivatives
The derivatives of inverse trigonometric functions are first-order derivatives. Let us check out the derivatives of all six inverse functions here.
| Inverse Trig Function | dy/dx |
| y = sin-1(x) | 1/√(1-x2) |
| y = cos-1(x) | -1/√(1-x2) |
| y = tan-1(x) | 1/(1+x2) |
| y = cot-1(x) | -1/(1+x2) |
| y = sec-1(x) | 1/[|x|√(x2-1)] |
| y = csc-1(x) | -1/[|x|√(x2-1)] |
Learn in detail the derivation of these functions here: Derivative Inverse Trigonometric Functions
Also read:
Inverse Trigonometric Functions Properties
The inverse trigonometric functions are also known as arc functions. Inverse trigonometric functions are defined in a certain interval (under restricted domains). Read more on inverse trigonometric properties here.
Trigonometry Basics
Trigonometry basics include the basic trigonometry and trigonometric ratios, such as sin x, cos x, tan x, cosec x, sec x and cot x.
Video Lessons on Inverse Trigonometric Functions
Inverse Trigonometric Functions

Multiple Angles

Inverse Trigonometric Functions Problems
Example 1: Find the value of x for sin(x) = 2.
Solution: Given: sin x = 2
x =sin-1(2), which is not possible.
Hence, there is no value of x for which sin x = 2, so the domain of sin-1x is -1 to 1 for the values of x.
Example 2: Find the value of sin-1(sin (π/6)).
Solution:
sin-1(sin (π/6) = π/6 (Using identity sin-1(sin (x) ) = x)
Example 3: Find sin (cos-1 3/5).
Solution:
Suppose that, cos-1 3/5 = x
So, cos x = 3/5
This implies, sin x = sin (cos-1 3/5) = 4/5
Example 4:
Solution:
Example 5:
Solution:
Example 6:
Solution:
Practice Problems
Problem 1: Solve: tan(arcsin 12/13)
Problem 2: Find the value of x, cos(arccos 1) = cos x
Learn more about inverse trigonometric functions at BYJU’S. Download BYJU’S – The Learning App for other Maths-related articles and access various interactive videos to make the subject easy.


Comments