JEE Main 2022 June 24 – Shift 2 Maths Question Paper with Solutions is given on this page. The detailed solutions of JEE Main 2022 Question Papers are prepared by our subject experts. The JEE Main 2022 answer keys will help students find the complete solution in a step-by-step method. Students can use the JEE Main 2022 question papers and solutions to scrutinize their performance in the JEE Main 2022 exam. The PDF format of JEE Main 2022 June 24 – Shift 2 Maths Question Paper with Solutions can also be downloaded for free from this page.
JEE Advanced 2019 Question Paper
JEE Main 2022 Maths Question Paper and Solutions – June 24th Shift 2
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. Let x * y = x2 + y3 and (x * 1) * 1 = x * (1 * 1). Then a value of \(\begin{array}{l}2\ sin^{-1}\left(\frac{x^4+x^2-2}{x^4+x^2+2}\right)\end{array} \)
is
\(\begin{array}{l}(A)\ \frac{\pi}{4}\end{array} \)
\(\begin{array}{l}(B)\ \frac{\pi}{3}\end{array} \)
\(\begin{array}{l}(C)\ \frac{\pi}{2}\end{array} \)
\(\begin{array}{l}(D)\ \frac{\pi}{6}\end{array} \)
Answer (B)
Sol. Given x * y = x2 + y3 and (x * 1) * 1 = x * (1 * 1)
So, (x2 + 1) * 1 = x * 2
⇒ (x2 + 1)2 + 1 = x2 + 8
⇒ x4 + 2x2 + 2 = x2 + 8
⇒ (x2)2 + x2 – 6 = 0
∴ (x2 + 3)(x2 – 2) = 0
∴ x2 = 2
Now,
\(\begin{array}{l}2 sin^{-1}\left(\frac{x^4+x^2-2}{x^4+x^2+2}\right)=2sin^{-1}\left(\frac{4}{8}\right)\end{array} \)
\(\begin{array}{l}=2.\frac{\pi}{6}=\frac{\pi}{3}\end{array} \)
2. The sum of all the real roots of the equation (e2x – 4)(6e2x – 5ex + 1) = 0 is
(A) loge3
(B) –loge3
(C) loge6
(D) –loge6
Answer (B)
Sol. Given equation : (e2x – 4)(6e2x – 5ex + 1) = 0
⇒ e2x – 4 = 0 or 6e2x – 5ex + 1 = 0
⇒ e2x = 4 or 6(ex)2 – 3ex – 2ex + 1 = 0
⇒ 2x = ln4 or (3ex – 1)(2ex – 1) = 0
\(\begin{array}{l}\Rightarrow x= In2\ or\ e^x=\frac{1}{3} or e^x=\frac{1}{2}\end{array} \)
or
\(\begin{array}{l}x=ln\frac{1}{3}, -ln2\end{array} \)
Sum of all real roots = ln2 – ln3 – ln2
= –ln3
3. Let the system of linear equations
x + y + az = 2
3x + y + z = 4
x + 2z = 1
have a unique solution (x*, y*, z*). If (α, x*), (y*, α) and (x*, –y*) are collinear points, then the sum of absolute values of all possible values of α is
(A) 4
(B) 3
(C) 2
(D) 1
Answer (C)
Sol. Given system of equations
x + y + az = 2 …(i)
3x + y + z = 4 …(ii)
x + 2z = 1 …(iii)
Solving (i), (ii) and (iii), we get
x = 1, y = 1, z = 0 (and for unique solution a ≠–3)
Now, (α, 1), (1, α) and (1, –1) are collinear
\(\begin{array}{l}\therefore \begin{vmatrix}\alpha &1 &1 \\1&\alpha &1 \\1 &-1 &1 \\\end{vmatrix}=0\end{array} \)
⇒ α(α + 1) – 1(0) + 1(–1 – α) = 0
⇒ α2 – 1 = 0
∴ α = ±1
∴ Sum of absolute values of α = 1 + 1 = 2
4. Let x, y > 0. If x3y2 = 215, then the least value of 3x + 2y is
(A) 30
(B) 32
(C) 36
(D) 40
Answer (D)
Sol. x, y > 0 and x3y2 = 215
Now,
\(\begin{array}{l}3x+2y=(x+x+x)+(y+y)\end{array} \)
So, by A.M G.M inequality
\(\begin{array}{l}\frac{3x+2y}{5}\geq \sqrt[5]{x^3.y^2}\end{array} \)
\(\begin{array}{l}\therefore 3x+2y\geq 5\sqrt[5]{2^{15}}\end{array} \)
\(\begin{array}{l}\geq 40\end{array} \)
∴ Least value of 3x + 4y = 40
5. Let \(\begin{array}{l}f(x)\left\{\begin{matrix} \frac{\sin(x-[x])}{x-[x]},& x \in (-2,-1)\\ \max{\left\{2x,3[\left|x \right|]\right\}},&\left|x \right|<1 \\ 1& ,\text{otherwise}& \\\end{matrix}\right. \end{array} \)
Where [t] denotes greatest integer t. If m is the number of points where f is not continuous and n is the number of points where f is not differentiable, then the ordered pair (m, n) is
(A) (3, 3)
(B) (2, 4)
(C) (2, 3)
(D) (3, 4)
Answer (C)
Sol.
\(\begin{array}{l}f(x)\left\{\begin{matrix} \frac{\sin(x-[x])}{x-[x]},& x \in (-2,-1)\\ \max{\left\{2x,3[\left|x \right|]\right\}},&\left|x \right|<1 \\ 1& ,\text{otherwise}& \\\end{matrix}\right. \end{array} \)
\(\begin{array}{l}\left\{\begin{matrix}\frac{sin(x+2)}{x+2} ,&x\in(-2,-1) \\0 , &x\in(-1, 0] \\2x ,&x\in(0, 1) \\1 , &othersiwe \\\end{matrix}\right.\end{array} \)
It clearly shows that f(x) is discontinuous
At x = –1, 1 also non differentiable and at x = 0,
L.H.D
\(\begin{array}{l}=\displaystyle \lim_{ h\to 0}\frac{f(0-h)-f(0)}{-h}=0\end{array} \)
R.H.D
\(\begin{array}{l}=\displaystyle \lim_{ h\to 0}\frac{f(0+h)-f(0)}{h}=2\end{array} \)
∴ f(x) is not differentiable at x = 0
∴ m = 2, n = 3
6. The value of the integral
\(\begin{array}{l}\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}}\frac{dx}{(1+e^x)(sin^6x+cos^6x)}\end{array} \)
is equal to
(A) 2π
(B) 0
(C) π
(D) π/2
Answer (C)
Sol.
\(\begin{array}{l}I=\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}}\frac{dx}{(1+e^x)(sin^6+cos^6x)}….(i)\end{array} \)
\(\begin{array}{l}I=\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}}\frac{dx}{(1+e^{-x})(sin^6 x+cos^6x)}…(ii)\end{array} \)
From equation (i) & (ii)
\(\begin{array}{l}2I=\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}}\frac{dx}{(sin^6x+cos^6x)}\end{array} \)
\(\begin{array}{l}\Rightarrow I=\int_{{0}}^{\frac{\pi}{2}}\frac{dx}{(sin^6x+cos^6x)}=\int_{{0}}^{\frac{\pi}{2}}\frac{dx}{1-\frac{3}{4}sin^2 2x}\end{array} \)
\(\begin{array}{l}\Rightarrow I=\int_{{0}}^{\frac{\pi}{2}}\frac{4sec^22xdx}{(4+tan^22x)}=2\int_{{0}}^{\frac{\pi}{4}}\frac{4sec^22x}{4+tan^22x}dx\end{array} \)
Now,
\(\begin{array}{l}tan2x=t\\2sec^22xdx=dt\end{array} \)
When x = 0, t = 0
When x = π/4, t →∞
\(\begin{array}{l}\therefore I=2\int_{0}^{\infty}\frac{2dt}{4+t^2}=2\left(tan^{-1}\frac{t}{2}\right )_{0}^{\infty}\end{array} \)
\(\begin{array}{l}=2\frac{\pi}{2}=\pi\end{array} \)
7. \(\begin{array}{l}\displaystyle \lim_{n\to \infty}\left(\frac{n^2}{(n^2+1)(n+1)}+\frac{n^2}{(n^2+4)(n+2)}+\frac{n^2}{(n^2+9)(n+3)}……+\frac{n^2}{(n^2+n^2)(n+n)}\right)\end{array} \)
is equal to
\(\begin{array}{l}(A)\ \frac{\pi}{8}+\frac{1}{4}log_e2\end{array} \)
\(\begin{array}{l}(B)\ \frac{\pi}{4}+\frac{1}{8}log_e2\end{array} \)
\(\begin{array}{l}(C)\ \frac{\pi}{4}-\frac{1}{8}log_e2\end{array} \)
\(\begin{array}{l}(D)\ \frac{\pi}{8}+\frac{1}{8}log_e\sqrt{2}\end{array} \)
Answer (A)
Sol.
\(\begin{array}{l}\displaystyle \lim_{n \to \infty}\left(\frac{n^2}{(n^2+1)(n+1)}+\frac{n^2}{(n^2+4)(n+2)}…..\frac{n^2}{(n^2+n^2)(n+n)}\right )\end{array} \)
\(\begin{array}{l}=\displaystyle \lim_{n\to\infty}\sum_{r=1}^{n}\frac{n^2}{(n^2+r^2)(n+r)}\end{array} \)
\(\begin{array}{l}=\displaystyle \lim_{n\to \infty}\sum_{r=1}^{n}\frac{1}{\left[1+\left(\frac{r}{n}\right)^2 \right ]\left[1+\left(\frac{r}{n}\right)\right]}\end{array} \)
\(\begin{array}{l}=\int_{0}^{1}\frac{1}{(1+x^2)(1+x)}dx\end{array} \)
\(\begin{array}{l}=\frac{1}{2}\int_{0}^{1}\left[\frac{1}{1+x}-\frac{(x-1)}{(1+x^2)} \right]dx\end{array} \)
\(\begin{array}{l}=\frac{1}{2}\left[In(1+x)-\frac{1}{2}In(1+x^2)+tan^{-1}x\right ]_{0}^{1}\end{array} \)
\(\begin{array}{l}=\frac{1}{2}\left[\frac{\pi}{4}+\frac{1}{2}In2\right]=\frac{\pi}{8}+\frac{1}{4}In2\end{array} \)
8. A particle is moving in the xy-plane along a curve C passing through the point (3, 3). The tangent to the curve C at the point P meets the x-axis at Q. If the y-axis bisects the segment PQ, then C is a parabola with
(A) Length of latus rectum 3
(B) Length of latus rectum 6
\(\begin{array}{l}(C)\ Focus\left(\frac{4}{3},0\right )\end{array} \)
\(\begin{array}{l}(D)\ Focus\left(0,\frac{3}{4}\right)\end{array} \)
Answer (A)
Sol. According to the question,
Let P(x,y)
\(\begin{array}{l}2x-y\frac{dx}{dy}=0\end{array} \)
\(\begin{array}{l}\begin{pmatrix}\because \text{equation of tangent at} \\P:y-y=\frac{dy}{dx}(y-x)\end{pmatrix}\end{array} \)
\(\begin{array}{l}\therefore 2\frac{dy}{y}=\frac{dx}{x} \end{array} \)
\(\begin{array}{l}\Rightarrow 2In y=In x + In c\end{array} \)
\(\begin{array}{l}\Rightarrow y^2=cx\end{array} \)
∵ This curve passes through (3, 3)
∴ c = 3
∴ Required parabola y2 = 3x and L.R = 3
9. Let the maximum area of the triangle that can be inscribed in the ellipse \(\begin{array}{l}\frac{x^2}{a^2}+\frac{y^2}{4}=1, a>2,\end{array} \)
having one of its vertices at one end of the major axis of the ellipse and one of its sides parallel to the y-axis, be 6√3. Then the eccentricity of the ellipse is
\(\begin{array}{l}(A)\ \frac{\sqrt{3}}{2}\end{array} \)
\(\begin{array}{l}(B)\ \frac{1}{2}\end{array} \)
\(\begin{array}{l}(C)\ \frac{1}{\sqrt{2}}\end{array} \)
\(\begin{array}{l}(D)\ \frac{\sqrt{3}}{4}\end{array} \)
Answer (A)
Sol.
Given ellipse
\(\begin{array}{l}\frac{x^2}{a^2}+\frac{y^2}{4}=1,a>2\end{array} \)
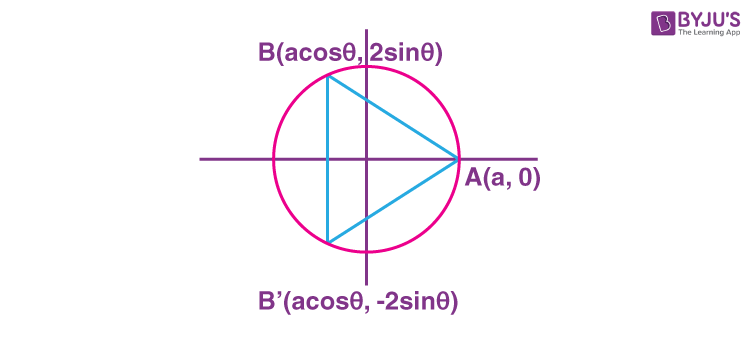
∴ Let A(θ) be the area of ΔABB′
Then
\(\begin{array}{l}A(\theta)=\frac{1}{2}4sin\theta(a+acos\theta)\end{array} \)
\(\begin{array}{l}A'(\theta)=a(2cos\theta+2cos^2\theta)\end{array} \)
For maxima A′(θ) = 0
\(\begin{array}{l}\Rightarrow cos\theta=-1, cos\theta=\frac{1}{2}\end{array} \)
But for maximum area
\(\begin{array}{l}cos\theta=\frac{1}{2}\end{array} \)
\(\begin{array}{l}\therefore A(\theta)=6\sqrt{3}\end{array} \)
\(\begin{array}{l}\Rightarrow 2\frac{\sqrt{3}}{2}\left(a+\frac{a}{2}\right)=6\sqrt{3}\end{array} \)
⇒ a = 4
\(\begin{array}{l}\therefore e=\sqrt{1-\frac{b^2}{a^2}}=\sqrt{1-\frac{4}{16}}=\frac{\sqrt{3}}{2}\end{array} \)
10. Let the area of the triangle with vertices A(1, α), B(α, 0) and C(0, α) be 4 sq. units. If the points (α, –α), (–α, α) and (α2, β) are collinear, then β is equal to
(A) 64
(B) –8
(C) –64
(D) 512
Answer (C)
Sol. ∵ A(1, α), B(α, 0) and C(0, α) are the vertices of ΔABC and area of ΔABC = 4
\(\begin{array}{l}\therefore \left|\frac{1}{2} \right|\begin{vmatrix}1 &\alpha &1 \\\alpha &0 &1 \\0 &\alpha &1 \\\end{vmatrix}=4\end{array} \)
\(\begin{array}{l}\Rightarrow \left|1(1-\alpha)-\alpha(\alpha)+\alpha^2\right|=8\end{array} \)
\(\begin{array}{l}\Rightarrow \alpha=\pm 8\end{array} \)
Now, (α, –α), (–α, α) and (α2, β) are collinear
\(\begin{array}{l}\therefore \begin{vmatrix}8 &-8 &1 \\-8 &8 &1 \\64 &\beta &1 \\\end{vmatrix}=0=\begin{vmatrix}-8 &8 &1 \\8 &-8 &1 \\64 &\alpha &1 \\\end{vmatrix}\end{array} \)
\(\begin{array}{l}\Rightarrow8(8-\beta)+8(-8-64)+1(-8\beta-8\times64)=0\end{array} \)
\(\begin{array}{l}\Rightarrow8-\beta-72-\beta-64=0\end{array} \)
\(\begin{array}{l}\Rightarrow\beta=-64\end{array} \)
11. The number of distinct real roots of the equation x7 – 7x – 2 = 0 is
(A) 5
(B) 7
(C) 1
(D) 3
Answer (D)
Sol. Given equation x7 – 7x – 2 = 0
Let f(x) = x7 – 7x – 2
f′(x) = 7x6 – 7 = 7(x6 – 1)
and f′(x) = 0 ⇒ x = +1
and f(–1) = –1 + 7 – 2 = 5 > 0
f(1) = 1 – 7 – 2 = –8 < 0
So, roughly sketch of f(x) will be
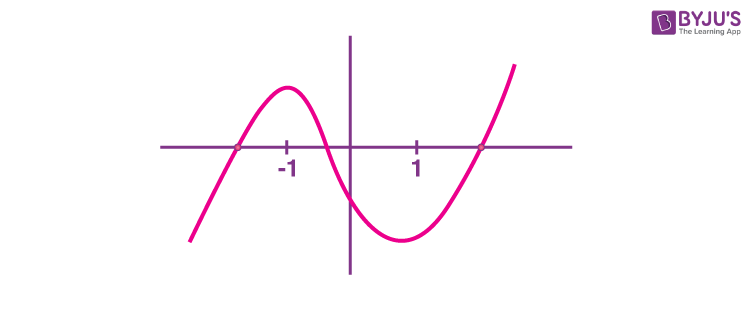
So, number of real roots of f(x) = 0 and 3.
12. A random variable X has the following probability distribution :
| X |
0 |
1 |
2 |
3 |
4 |
| P(X) |
k |
2k |
4k |
6k |
8k |
The value of P(1 < X < 4 | x ≤ 2) is equal to
\(\begin{array}{l}(A)\ \frac{4}{7}\end{array} \)
\(\begin{array}{l}(B)\ \frac{2}{3}\end{array} \)
\(\begin{array}{l}(C)\ \frac{3}{7}\end{array} \)
\(\begin{array}{l}(D)\ \frac{4}{5}\end{array} \)
Answer (A)
Sol.
∵ x is a random variable
∴ k + 2k + 4k + 6k + 8k = 1
\(\begin{array}{l}\therefore k=\frac{1}{21}\end{array} \)
Now,
\(\begin{array}{l}P\left(1<x<4)|x\leq2 \right)=\frac{4k}{7k}=\frac{4}{7}\end{array} \)
13. The number of solutions of the equation \(\begin{array}{l}cos\left ( x+\frac{\pi}{3} \right)cos\left (\frac{\pi}{3}-x\right)=\frac{1}{4}cos^22x,x\in[-3\pi,3\pi]\end{array} \)
is:
(A) 8
(B) 5
(C) 6
(D) 7
Answer (D)
Sol.
\(\begin{array}{l}cos\left ( x+\frac{\pi}{3} \right)cos\left (\frac{\pi}{3}-x\right)=\frac{1}{4}cos^22x,x\in[-3\pi,3\pi]\end{array} \)
\(\begin{array}{l}\Rightarrow cos2x+cos\frac{2\pi}{3}=\frac{1}{2}cos^22x\end{array} \)
\(\begin{array}{l}\Rightarrow cos^22x-2cos2x-1=0\end{array} \)
\(\begin{array}{l}\Rightarrow cos2x=1\end{array} \)
\(\begin{array}{l}\therefore x=-3\pi,-2\pi,-\pi,0,\pi,2\pi,3\pi\end{array} \)
∴ Number of solutions = 7
14. If the shortest distance between the lines \(\begin{array}{l}\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{\lambda}~\text{and}~ \frac{x-2}{1}=\frac{y-4}{4}=\frac{z-5}{5}\end{array} \)
is 1/√3, then the sum of all possible values of λ is :
(A) 16
(B) 6
(C) 12
(D) 15
Answer (A)
Sol. Let
\(\begin{array}{l}\vec{a}_1=\hat{i}+2\hat{j}+3\hat{k}\end{array} \)
\(\begin{array}{l}\vec{a}_2=2\hat{i}+4\hat{j}+5\hat{k}\end{array} \)
\(\begin{array}{l}\vec{p}=2\hat{i}+3\hat{j}+\lambda\hat{k},\vec{q}=\hat{i}+4\hat{j}+5\hat{k} \end{array} \)
\(\begin{array}{l}\therefore \vec{p}\times\vec{q}=(15-4\lambda)\hat{i}-(10-\lambda)\hat{j}+5\hat{k}\end{array} \)
\(\begin{array}{l}\vec{a}_2-\vec{a}_1=\hat{i}+2\hat{j}+2\hat{k}\end{array} \)
∴ Shortest distance
\(\begin{array}{l}=\left|\frac{(15-4\lambda)-2(10-\lambda)+10)}{\sqrt{(15-4\lambda)^2+(10-\lambda)^2+25}}\right|=\frac{1}{\sqrt{3}}\end{array} \)
\(\begin{array}{l}\Rightarrow 3(5-2\lambda)^2=(15-4\lambda)^2+(10-\lambda)^2+25\end{array} \)
\(\begin{array}{l}\Rightarrow 5\lambda^2-80\lambda+275=0\end{array} \)
\(\begin{array}{l}\therefore \text{Sum of values of}\ \lambda=\frac{80}{5}=16\end{array} \)
15. Let the points on the plane P be equidistant from the points (–4, 2, 1) and (2, –2, 3). Then the acute angle between the plane P and the plane 2x + y + 3z = 1 is
\(\begin{array}{l}(A)\ \frac{\pi}{6}\end{array} \)
\(\begin{array}{l}(B)\ \frac{\pi}{4}\end{array} \)
\(\begin{array}{l}(C)\ \frac{\pi}{3}\end{array} \)
\(\begin{array}{l}(D)\ \frac{5\pi}{12}\end{array} \)
Answer (C)
Sol.
Let P(x, y, z) be any point on plane P1
Then
\(\begin{array}{l}(x+4)^2+(y-2)^2+(z-1)^2=(x-2)^2+(y+2)^2+(z-3)^2\end{array} \)
\(\begin{array}{l}\Rightarrow 12x-8y+4z+4=0 \end{array} \)
\(\begin{array}{l}\Rightarrow 3x-2y+z+1=0 \end{array} \)
And P2 : 2x + y + 3z = 1
∴ angle between P1 and P2
\(\begin{array}{l}Cos~\theta=\left|\frac{6-2+3}{14}\right|\Rightarrow\theta=\frac{\pi}{3}\end{array} \)
16. \(\begin{array}{l}\text{Let}\ \hat{a}\ \text{and}\ \hat{b}\ \text{be two unit vectors such that}\end{array} \)
\(\begin{array}{l}\left|(\hat{a}+\hat{b})+2(\hat{a}\times\hat{b}) \right|=2. \end{array} \)
If θ ∈ (0, π) is the angle between \(\begin{array}{l}\hat{a}\ \text{and}\ \hat{b},\ \text{then among the statements}:\end{array} \)
(S1):
\(\begin{array}{l}2\left|\hat{a}\times\hat{b}\right|=\left|\hat{a}-\hat{b} \right| \end{array} \)
(S2): The projection of
\(\begin{array}{l}\hat{a}\ \text{on}\ (\hat{a}+\hat{b})is \frac{1}{2}\end{array} \)
(A) Only (S1) is true
(B) Only (S2) is true
(C) Both (S1) and (S2) are true
(D) Both (S1) and (S2) are false
Answer (C)
Sol.
\(\begin{array}{l}\because \left|\hat{a}+\hat{b}+2(\hat{a}\times \hat{b})\right|=2,\theta\in(0,\pi) \end{array} \)
\(\begin{array}{l}\Rightarrow \left|\hat{a}+\hat{b}+2(\hat{a}\times \hat{b}) \right|^2=4.\end{array} \)
\(\begin{array}{l}\Rightarrow \left|\hat{a}\right|^2+\left|\hat{b}\right|^2+4\left|\hat{a}\times \hat{b}\right|^2+2\hat{a}.\hat{b}=4.\end{array} \)
\(\begin{array}{l}\therefore cos\theta=cos2\theta \end{array} \)
\(\begin{array}{l}\therefore \theta=\frac{2\pi}{3}\end{array} \)
\(\begin{array}{l}\text{where}\ \theta\ \text{is angle between}\ \hat{a}\end{array} \)
and \(\begin{array}{l}\hat{b}.\end{array} \)
\(\begin{array}{l}\therefore 2\left|\hat{a}\times \hat{b} \right|=\sqrt{3}=\left|\hat{a}- \hat{b} \right|\end{array} \)
(S1) is correct
\(\begin{array}{l}\text{And projection of}\ hat{a}\ \text{on}\ (\hat{a}+\hat{b})=\left|\frac{\hat{a}.(\hat{a}+\hat{b})}{\left|\hat{a}+\hat{b}\right|}\right|=\frac{1}{2}.\end{array} \)
(S2) is correct.
17. If \(\begin{array}{l}y=tan^{-1}(sec~ x^3-tan~x^3),\frac{\pi}{2}<x^3<\frac{3\pi}{2},\end{array} \)
then
(A) xy′′ + 2y′ = 0
\(\begin{array}{l}(B)\ x^2y”-6y+\frac{3\pi}{2}=0\end{array} \)
(C) x2y″ – 6y + 3π = 0
(D) xy″ – 4y′ = 0
Answer (B)
Sol.
\(\begin{array}{l}Let~ x^3=\theta\Rightarrow\frac{\theta}{2}\in \left(\frac{\pi}{4},\frac{3\pi}{4}\right )\end{array} \)
∴ y = tan–1 (secθ – tanθ)
\(\begin{array}{l}=tan^{-1}\left(\frac{1-sin~\theta}{cos~\theta}\right)\end{array} \)
\(\begin{array}{l}\therefore y=\frac{\pi}{4}-\frac{\theta}{2}. \end{array} \)
\(\begin{array}{l}y=\frac{\pi}{4}-\frac{x^3}{2}\end{array} \)
\(\begin{array}{l}\therefore y’=\frac{-3x^2}{2}\end{array} \)
y″ = – 3x
\(\begin{array}{l}\therefore x^2y”-6y+\frac{3\pi}{2}=0.\end{array} \)
18. Consider the following statements:
A : Rishi is a judge.
B : Rishi is honest.
C : Rishi is not arrogant.
The negation of the statement “if Rishi is a judge and he is not arrogant, then he is honest” is
(A) B → (A ∨ C)
(B) (~ B) ∧ (A ∧ C)
(C) B → ((~ A) ∨ (~ C))
(D) B → (A ∧ C)
Answer (B)
Sol. ∵given statement is
(A ∧ C) → B
Then its negation is
~ {(A ∧ C) → B}
or ~ {~ (A ∧ C) ∨ B}
∴ (A ∧ C) ∧ (~ B)
or (~ B) ∧ (A ∧ C)
19. The slope of normal at any point (x, y), x > 0, y > 0 on the curve y = y(x) is given by \(\begin{array}{l}\frac{x^2}{xy-x^2y^2-1}.\end{array} \)
If the curve passes through the point (1, 1), then e · y(e) is equal to
\(\begin{array}{l}(A)\ \frac{1-tan(1)}{1+tan(1)}\end{array} \)
(B) tan(1)
(C) 1
\(\begin{array}{l}(D)\ \frac{1+tan(1)}{1-tan(1)}\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l}\because -\frac{dx}{dy}=\frac{x^2}{xy-x^2y^2-1} \end{array} \)
\(\begin{array}{l}\therefore \frac{dy}{dx}=\frac{x^2y^2-xy+1}{x^2} \end{array} \)
\(\begin{array}{l}\text{Let}\ xy=v\Rightarrow y+x\frac{dy}{dx}=\frac{dv}{dx}\end{array} \)
\(\begin{array}{l}\therefore \frac{dv}{dx}-y=\frac{(v^2-v+1)y}{v}\end{array} \)
\(\begin{array}{l}\therefore \frac{dv}{dx}=\frac{v^2+1}{x}\end{array} \)
∵ y(1) = 1 ⇒ tan–1 (xy) = lnx + tan–1(1)
Put x = e and y = y(e) we get
tan–1 (e · y(e)) = 1 + tan–1 1.
tan–1 (e · y(e)) – tan–1 1 = 1
\(\begin{array}{l}\therefore e(y(e))=\frac{1+tan(1)}{1-tan(1)}\end{array} \)
20. Let λ* be the largest value of λ for which the function fλ(x) = 4λx3 – 36λx2 + 36x + 48 is increasing for all x ∈ ℝ. Then fλ* (1) + fλ* (– 1) is equal to :
(A) 36
(B) 48
(C) 64
(D) 72
Answer (D)
Sol. ∵ fλ(x) = 4λx3 – 36λx2 + 36x + 48
\(\begin{array}{l}\therefore f_{\lambda }^{‘}(x)=12(\lambda x^2-6\lambda x+3) \end{array} \)
For fλ(x) increasing : (6λ)2 – 12λ ≤ 0
\(\begin{array}{l}\therefore \lambda\in \left[0,\frac{1}{3}\right ]\end{array} \)
\(\begin{array}{l}\therefore \lambda^*=\frac{1}{3}\end{array} \)
Now,
\(\begin{array}{l}f_\lambda^{*}(x)=\frac{4}{3}x^3-12x^2+36x+48\end{array} \)
\(\begin{array}{l}\therefore f_{\lambda }^{*}+f_{\lambda}^{*}(-1)=73\frac{1}{2}-1\frac{1}{2} \end{array} \)
= 72.
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, –00.33, –00.30, 30.27, –27.30) using the mouse andw the on-screen virtual numeric keypad in the place designated to enter the answer.
1. \(\begin{array}{l}\text{Let}\ S={z\in\mathbb{C}:\left|z-3 \right|}\leq1\ \text{and}\ z(4~+~3{i})+{\overline{z}(4-3i)\leq 24}.\end{array} \)
If α + iβ is the point in S which is closest to 4i, then 25(α + β) is equal to ______.
Answer (80)
Sol. Here |z – 3| < 1
⇒ (x – 3)2 + y2 < 1
And
\(\begin{array}{l}z=(4+3i)+\bar{z}(4-3i)\leq 24\end{array} \)
\(\begin{array}{l}\Rightarrow 4x-3y\leq 12\end{array} \)
\(\begin{array}{l}tan\theta=\frac{4}{3}\end{array} \)
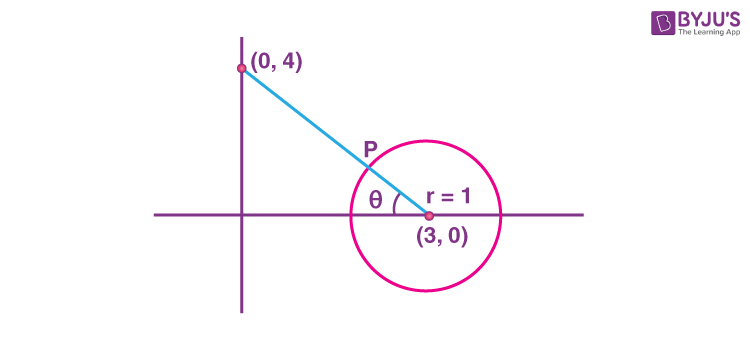
∴ Coordinate of P = (3 – cosθ, sinθ)
\(\begin{array}{l}=\left ( 3-\frac{3}{5},\frac{4}{5} \right )\end{array} \)
\(\begin{array}{l}\therefore \alpha+i\beta=\frac{12}{5}+\frac{4}{5}i \end{array} \)
\(\begin{array}{l}\therefore 25(\alpha+\beta)=80 \end{array} \)
2. Let \(\begin{array}{l}S = \begin{Bmatrix}\begin{pmatrix}-1 &a\\0 &b \\\end{pmatrix},a, b \in (1,2,3,….100)\\\end{Bmatrix}\end{array} \)
and let Tn = {A ∈ S : An(n + 1) = I}. Then the number of elements in \(\begin{array}{l}\bigcap_{n=1}^{100}T_n\ \text{is}—–.\end{array} \)
Answer (100)
Sol.
\(\begin{array}{l}S=\begin{Bmatrix}\begin{pmatrix}-1 &a\\0 &b \\\end{pmatrix}:a,b\in{1,2,3,…,100}\\\end{Bmatrix}\end{array} \)
\(\begin{array}{l}\therefore A=\begin{pmatrix}-1 &a \\0 &b \\\end{pmatrix}\end{array} \)
then even powers of A as
\(\begin{array}{l}A \begin{pmatrix}1 &0 \\0 &1 \\\end{pmatrix},\end{array} \)
if b = 1 and a ∈ {1,….., 100}
Here, n(n + 1) is always even.
∴ T1, T2, T3, …, Tn are all I for b = 1 and each value of a.
\(\begin{array}{l}\therefore \bigcap_{n=1}^{100}T_n=100 \end{array} \)
3. The number of 7-digit numbers which are multiples of 11 and are formed using all the digits 1, 2, 3, 4, 5, 7 and 9 is _____.
Answer (576)
Sol. Sum of all given numbers = 31
Difference between odd and even positions must be 0, 11 or 22, but 0 and 22 are not possible.
∴ Only difference 11 is possible
This is possible only when either 1, 2, 3, 4 is filled in odd position in some order and remaining in other order. Similar arrangements of 2, 3, 5 or 7, 2, 1 or 4, 5, 1 at even positions.
∴ Total possible arrangements = (4! × 3!) × 4
= 576
4. The sum of all the elements of the set {α ∈ {1, 2, …, 100} : HCF(α, 24) = 1} is
Answer (1633)
Sol. The numbers upto 24 which gives g.c.d. with 24 equals to 1 are 1, 5, 7, 11, 13, 17, 19 and 23.
Sum of these numbers = 96
There are four such blocks and a number 97 is there upto 100.
∴ Complete sum
= 96 + (24 × 8 + 96) + (48 × 8 + 96) + (72 × 8 + 96) + 97
= 1633
5. The remainder on dividing 1 + 3 + 32 + 33 + … + 32021 by 50 ____ is
Answer (4)
Sol.
\(\begin{array}{l}1+3+3^2+….+3^{2021}=\frac{3^{2022}-1}{2}\end{array} \)
\(\begin{array}{l}=\frac{1}{2}\begin{Bmatrix}(10-1)^{1011}-1\end{Bmatrix}\end{array} \)
\(\begin{array}{l}=\frac{1}{2}\begin{Bmatrix}{100k+10110-1-1}\end{Bmatrix}\end{array} \)
= 50 k1 + 4
∴ Remainder = 4
6. The area (in sq. units) of the region enclosed between the parabola y2 = 2x and the line x + y = 4 is _______.
Answer (18)
Sol.
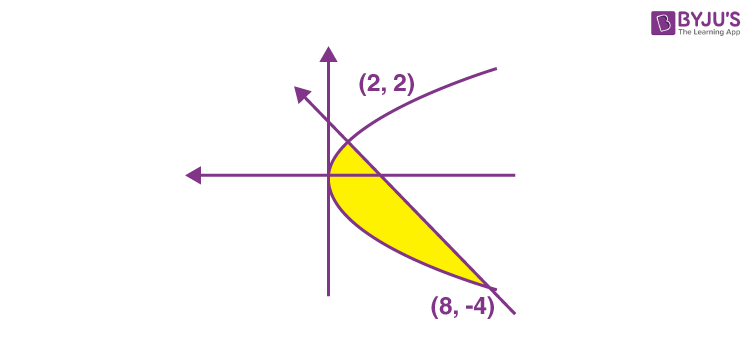
The required area
\(\begin{array}{l}=\int_{-4}^{2}\begin{pmatrix}4-y-\frac{y^2}{2}\end{pmatrix}dy\end{array} \)
\(\begin{array}{l}=\begin{bmatrix}4y-\frac{y^2}{2}-\frac{y^3}{6}\end{bmatrix}_{-4}^{2}\end{array} \)
= 18 square units
7. Let a circle C : (x – h)2 + (y – k)2 = r2, k > 0, touch the x-axis at (1, 0). If the line x + y = 0 intersects the circle C at P and Q such that the length of the chord PQ is 2, then the value of h + k + r is equal to ____.
Answer (7)
Sol.

Here, OM2 = OP2 – PM2
\(\begin{array}{l}\begin{pmatrix}\left|\frac{1+r}{\sqrt{2}}\right|\end{pmatrix}^{2}=r^2-1\end{array} \)
∴ r2 – 2r – 3 = 0
∴ r = 3
∴ Equation of circle is
\(\begin{array}{l}(x-1)^2+(y-3)^2=3^2\end{array} \)
∴ h = 1, k = 3, r = 3
∴ h + k + r = 7
8. In an examination, there are 10 true-false type questions. Out of 10, a student can guess the answer of 4 questions correctly with probability 3/4and the remaining 6 questions correctly with probability ¼. If the probability that the student guesses the answers of exactly 8 questions correctly out of 10 is \(\begin{array}{l}\frac{27k}{4^{10}},\end{array} \)
then k is equal to
Answer (479)
Sol. Student guesses only two wrong. So there are three possibilities
(i) Student guesses both wrong from 1st section
(ii) Student guesses both wrong from 2nd section
(iii) Student guesses two wrong one from each section
Required probabilities
\(\begin{array}{l}=4C_2\left ( \frac{3}{4} \right )^2\left ( \frac{1}{4} \right )^2\left ( \frac{1}{4} \right )^6+ 6C_2\left ( \frac{3}{4} \right )^2\left ( \frac{1}{4} \right )^4\left ( \frac{1}{4} \right )^4+4C_1.6C_1\left ( \frac{3}{4} \right )\left ( \frac{1}{4} \right )\left ( \frac{3}{4} \right )^3\left ( \frac{1}{4} \right )^5\end{array} \)
\(\begin{array}{l}=\frac{1}{4^{10}}\left [ 6\times9+15\times9^4+24\times9^2 \right]\end{array} \)
\(\begin{array}{l}=\frac{27}{4^{10}}\left[2+27\times15+72 \right]\end{array} \)
\(\begin{array}{l}=\frac{27\times479}{4^{10}}\end{array} \)
9. Let the hyperbola \(\begin{array}{l}H:\frac{x^2}{a^2}-y^2=1\end{array} \)
and the ellipse \(\begin{array}{l}E:3x^2+4y^2=12\end{array} \)
be such that the length of latus rectum of H is equal to the length of latus rectum of E. If eH and eE are the eccentricities of H and E respectively, then the value of \(\begin{array}{l}12\left(e_H^2+e_E^2\right)\ \text{is equal to}——–.\end{array} \)
Answer (42)
Sol.
\(\begin{array}{l}\because H:\frac{x^2}{a^2}-\frac{y^2}{1}=1 \end{array} \)
∴ Length of latus rectum
\(\begin{array}{l}=\frac{2}{a}\end{array} \)
\(\begin{array}{l}E:\frac{x^2}{4}+\frac{y^2}{3}=1\end{array} \)
Length of latus rectum
\(\begin{array}{l}=\frac{6}{2}=3\end{array} \)
\(\begin{array}{l}\because \frac{2}{a}=3\Rightarrow a=\frac{2}{3} \end{array} \)
\(\begin{array}{l}12\left (e _{H}^{2}+e_{E}^{2}\right )=12\left ( 1+\frac{9}{4} \right )+\left ( 1-\frac{3}{4} \right )=42\end{array} \)
10. Let P1 be a parabola with vertex (3, 2) and focus (4, 4) and P2 be its mirror image with respect to the line x + 2y = 6. Then the directrix of P2 is x + 2y = _______.
Answer (10)
Sol. Focus = (4, 4) and vertex = (3, 2)
∴ Point of intersection of directrix with axis of parabola = A = (2, 0)
Image of A(2, 0) with respect to line
x + 2y = 6 is B(x2, y2)
\(\begin{array}{l}\therefore \frac{x_2-2}{1}=\frac{y_2-0}{2}=\frac{-2(2+0-6)}{5} \end{array} \)
\(\begin{array}{l}\therefore B(x_2,y_2)=\left ( \frac{18}{5},\frac{16}{5} \right ).\end{array} \)
Point B is point of intersection of direction with axes of parabola P2.
∴ x + 2y = λ must have point
\(\begin{array}{l}\left ( \frac{18}{5},\frac{16}{5} \right )\end{array} \)
∴ x + 2y = 10
JEE Main 2022 June 24th Shift 2 Question Paper with Solutions
JEE Main 2022 June 24 Shift 2 Question Paper – Physics Solutions
JEE Main 2022 June 24 Shift 2 Question Paper – Chemistry Solutions
JEE Main 2022 June 24 Shift 2 Question Paper – Maths Solutions
Frequently Asked Questions – FAQs
Q1
How many questions are there in JEE Main 2022 June 24 Shift 2 Maths question paper?
There are 30 questions in JEE Main 2022 June 24 Shift 2 question paper.
Q2
What is the difficulty level of JEE Main 2022 24th June Shift 2 Maths question paper?
The difficulty level of JEE Main 2022 June 24 Shift 2 Maths question paper is 1.90 out of 3. The questions were difficult comparing Physics and Chemistry papers.
Q3
How many questions were asked from class 12 in JEE Main 2022 Shift 2 June 24 Maths question paper?
11 questions were asked from class 12 in Maths paper as per the memory-based question paper.
Q4
What is the difficulty level of questions asked from the chapter Sequences and Series?
The questions from the chapter Sequences and Series were easy.
Q5
How were the questions from Integrals in JEE Main Shift 2 June 24 Maths question paper 2022?
The questions from Integrals were quite difficult.

















Comments