1. The region represented by {z = x+iy ∈ C : z -Re(z) ≤1} is also given by the inequality: {z = x + iy ∈ C : z -Re(z) ≤ 1}
1) y2≤2(x+1/2)
2) y2≤ x+(1/2)
3) y2 2(x+1)
4) y2 (x+1)
{z = x + iy ∈ C : z -Re(z) ≤ 1}
|z| = v(x2+y2)
Re(z) = x
z- Re(z) ≤1
⇒ v(x2+y2)-x≤1
⇒ v(x2+y2)≤1+x
⇒ (x2+y2)≤1+x2+2x
⇒ y2≤ 2(x+1/2)
Answer: (1)
2. The negation of the Boolean expression p (~p∧q) is equivalent to:
1) p∧~q
2) ~p~q
3) ~pq
4) ~p∧~q
pV (~p∧q)
(pV p) ∧ (pVq)
t∧(pV q)
pVq
~(pV(~ p∧q)) = ~ (pVq)
= (~ p)∧(~ q)
Answer: (4)
3. The general solution of the differential equation v(1+x2+y2+x2y2)+xy(dy/dx) = 0
(where C is a constant of integration)
1)
2)
3)
4)

1+y2 = z2
2ydy = 2zdz
((t2-1+1)/(t2-1) )dt = -z+c
1dt+(1/t2-1)dt = -z+c
t+(1/2)ln((t-1)/(t+1)) = -z+c
v(1+x2)+(1/2)ln(v(1+x2)-1/(v(1+x2 )+1) = -v(1+y2)+c
v(1+y2)+ v(1+x2) = (½)ln(v(1+x2)+1)/(v(1+x2 )-1))+c
Answer: (3)
4. Let L1 be a tangent to the parabola y2 = 4(x+1) and L2 be a tangent to the parabola y2 = 8(x+2) such that L1 and L2 intersect at right angles. Then L1 and L2 meet on the straight line:
1) x+2y = 0
2) x+2 = 0
3) 2x+1 = 0
4) x+3 = 0
Let t1 tangent of y2 = 4(x+1)
L1 : t1y = (x+1)+t12 …….(i)
and t2 tangent of y2 = 8(x+2)
L2 : t2y = (x+2)+2t22 ….(ii)
L1 perpendicular to L2
(1/t1)(1/t2) = -1
t1t2 = -1
t2(i) -t1(ii)
t1t2y = t2(x+1)+ t2. t12
t1t2y = t1(x+2)+2t22. t1
Subtracting above equations
(t2-t1) x+(t2-2t1) + t2t1(t1-2t2) = 0
(t2– t1)x +(t2-2t1)-(t1-2t2) = 0
(t2 -t1) x + 3t2-3t1 = 0
⇒ x+3 = 0
Answer: (4)
5. The area (in sq. units) of the region A = {(x, y): |x|+|y| ≤ 1, 2y2|x|}
1) 1/6
2) 5/6
3) 1/3
4) 7/6

Total area =
=
= 4[(1/2)-(1/8)-(v2/3)(1/2)3/2]
= 4×5/24
= 5/6
Answer: (2)
6. The shortest distance between the lines (x-1)/0 = (y+1)/-1 = z/1 and x+y+z+1 = 0, 2x-y+z+3 = 0 is:
1) 1
2) 1/v2
3) 1/v3
4) ½
Plane through line of intersection is
x+y+z+1+λ(2x-y+z+3) = 0
It should be parallel to given line
0(1+2λ)-1(1-λ)+1(1 +λ) = 0
⇒ λ = 0
Plane: x+y+z+1 = 0
Shortest distance of (1,-1,0) from this plane
= 1-1+0+1/v(12+12+12)
= 1/v3
Answer: (3)
7. Let a, b, c, d and p be any non zero distinct real numbers such that (a2+b2+c2)p2-2(ab+bc+cd)p +(b2 +c2+d2) = 0. Then:
1) a, c, p are in G.P.
2) a, b, c, d are in G.P.
3) a, b, c, d are in A.P.
4) a, c, p are in A.P.
(a2+b2+c2)p2-2(ab+bc+cd)p +(b2 +c2+d2) = 0
(a2p2-2abp+b2]+[b2p2-2bcp+c2]+[ c2p2-2cdp+d2] = 0
(ap-b)2+(bp -c)2+(cp-d)2 = 0
ap = b
bp = c
cp = d
b/a = c/b = d/c = p
a, b, c, d are in G.P.
Answer: (2)
8. Two families with three members each and one family with four members are to be seated in a row. In how many ways can they be seated so that the same family members are not separated?
1) 2! 3! 4!
2) (3!)3(4!)
3) 3!(4!)3
4) (3!)2(4!)
Total numbers in three families = 3+3+4 = 10
So total arrangement = 10!

Favourable cases
= Arrangement of 3 families × Interval arrangement of family members
= 3!×3!×3!×4!
= (3!)3(4!)
Answer: (2)
9. The values of λ and μ for which the system of linear equations
x+y+z = 2
x+2y+3z = 5
x+3y+λz = μ
has infinitely many solutions are, respectively:
1) 6 and 8
2) 5 and 8
3) 5 and 7
4) 4 and 9
x+y+z = 2
x+2y+3z = 5
x+3y+λz = μ
has infinitely many solutions
Δ =
R2 → R2-R1
R3 → R3-R1
⇒
(λ-1-4) = 0
λ = 5
Δ3 =
R2 → R2-R1
R3 → R3-R1
⇒
(μ-2-6) = 0
⇒ μ = 8
λ = 5, μ = 8
Answer: (2)
10. Let m and M be respectively the minimum and maximum values of
Then the ordered pair (m, M) is equal to:
1) (-3, -1)
2) (-4, -1)
3) (1, 3)
4) (-3, 3)
R1 → R1-R2
R3→ R3-R2
⇒ -1(sin2x) -1(1+cos2x +sin2x)
⇒ -sin2x –cos2x -1- sin2x
= -2-sin2x
So minimum value when sin2x = 1
m = -2-1 = -3
So maximum value when sin2x = -1
(m, M) = (-3, -1)
Answer: (1)
11. A ray of light coming from the point (2, 2v3) is incident at an angle 300 on the line x = 1 at the point A. The ray gets reflected on the line x = 1 and meets x-axis at the point B. Then, the line AB passes through the point:
1) (4,-v3)
2) (3, -1/v3)
3) (3,-v3)
4) (4, -v3/2)

Equation of line P’B passing through (0, 2v3)
(y-y1) = m (x-x1)
(y-2v3) = tan 1200 (x- 0)
y-2v 3 = -v3x
v3 x+y = 2v 3
Check options
(3,-v3) satisfy the line.
Answer: (3)
12. Out of 11 consecutive natural numbers if three numbers are selected at random (without repetition), then the probability that they are in A.P. with positive common difference, is:
1) 10/99
2) 5/33
3) 15/101
4) 5/101
Case-1
E, O, E, O, E, O, E, O, E, O, E
2b = a+c → Even
⇒ Both a and c should be either even or odd.
P = (6C2+5C2 )/ 11C3 = 5/33
Case -2
O, E, O, E, O, E, O, E, O, E, O
P = (5C2+6C2 )/ 11C3 = 5/33
Total probability = (1/2)×(5/33)+(1/2)×(5/33)
= 5/33
Answer: (2)
13. If f(x + y) = f(x) f(y) and
1) 2/3
2) 1/9
3) 1/3
4) 4/9
f(x + y) = f(x) f(y)
Put x = 1, y = 1
f(2) = (f(1))2
Put x = 2, y = 1
f(3) = f(2). f(1) = f((1))3
Put x = 2, y = 2
f(4) = f((2))2 = f((1))4
f(n) = (f(1))n
⇒ f(1)+f((1))2+f(1))3+… = 2
f(1)/(1-f(1)) = 2
f(1) = 2/3
f(2) = (2/3)2
f(4) = (2/3)4
f(4)/f(2) = (2/3)4(2/3)2 = 4/9
Answer: (4)
14. If {p} denotes the fractional part of the number p, then {3200/8} is equal to:
1) 5/8
2) 1/8
3) 7/8
4) 3/8
{3200/8} = {9100/8} = {(8+1)100/8}
{(100C0 1100+100C1 (8)199+100C2 (82)198+…100C100 8100)/8}
= {(100C0 1100+8k)/8}
= {(1+8k)/8}
= {(1/8)+k} k∈I
= 1/8
Answer: (2)
15. Which of the following points lies on the locus of the foot of perpendicular drawn upon any tangent to the ellipse (x2/4)+(y2/2) = 1 from any of its foci ?
1) (-1,v3)
2) (-2, v3)
3) (-1, v2)
4) (1,2)
Let foot of perpendicular is (h,k)

(x2/4)+(y2/2) = 1 (Given)
a = 2, b = v2
e = v(1-2/4)
= 1/v2
So focus (ae,0) = (v2,0)
Equation of tangent
y = mx+v(a2m2+b2)
y = mx+v(4m2+2)
Passes through (h,k) (k -mh)2 = 4m2+2
line perpendicular to tangent will have slope -1/m
y-0 = -(1/m)(x-v2)
my = -x+v2
(h+mk)2 = 2
Add equation (1) and (2)
k2(1+m2)+h2(1+m2) = 4(1+m2)
h2+k2 = 4
x2+y2 = 4 (auxiliary circle)
(-1,v3) lies on the locus.
Answer: (1)
16.
1) is equal to 1
2) is equal to 1/2
3) does not exist
4) is equal to -1/2
Using L hospital rule
=

On taking limit
= 0/(1+1)
= 0
Answer: Bouns
17. If
1) nv(a-1)
2) v(na-1)
3) a-1
4) v(a-1)
S.D =
=
Answer: (4)
18. If α and β be two roots of the equation x2 -64x+256 = 0. Then the value of (α3/β5)1/8+(β3/α5)1/8 is:
1) 1
2) 3
3) 2
4) 4
x2 -64x+256 = 0.
αβ = 256
α+β = 64
(α3/β5)1/8+(β3/α5)1/8
= (α+β)/(αβ)5/8
= 64/(256)5/8
= 64/32
= 2
Answer: (3)
19. The position of a moving car at time t is given by f(t) = at2+bt+c, t > 0, where a, b and c are real numbers greater than 1. Then the average speed of the car over the time interval [t1, t2] is attained at the point :
1) (t1+t2)/2
2) 2a(t1+t2)+b
3) (t2-t1)/2
4) a(t2-t1)+b
f’(t) = Vav = f(t2)-f(t1)/(t2-t1)
= [a(t22-t12)+b(t2-t1)]/(t2-t1)
= a(t1+t2)+b
= 2at+b
t = (t1+t2)/2
Answer: (1)
20. If
1) 5050/5049
2) 5050/5051
3) 5051/5050
4) 5049/5050
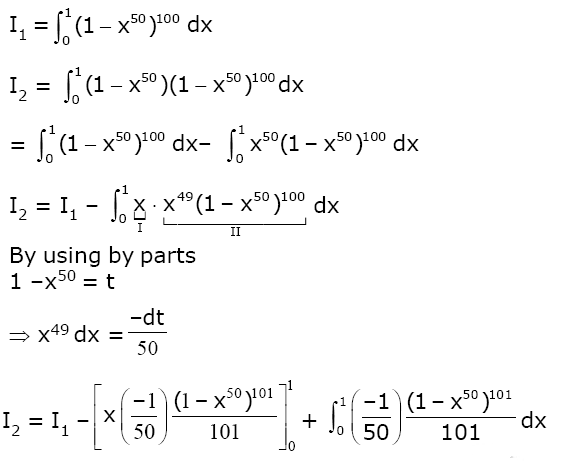
I2 =
I2 = I1-I2/5050
(5051/5050)I2 = I1
I2 = (5050/5051)I1
α = 5050/5051
Answer: (2)
21. If
= v3(v(2+2cos?)+v(2-2cos?)
= v6(v(1+cos?)+v2(1-cos?)
= v6(v(1+2cos2 (?/2)-1)+v2(v(1-1+2sin2 ?/2)
= v6(v(2cos2?/2)+v2(v(2sin2?/2))
{ greatest value of trigonometric function a cos?+b sin? ≤v(a2+b2)}
= 2v3cos(?/2)+2sin?/2
≤ v(2v3)2+(2)2
= 4
Answer: 4
22. Let AD and BC be two vertical poles at A and B respectively on a horizontal ground. If AD = 8 m, BC = 11 m and AB = 10 m; then the distance (in meters) of a point M on AB from the point A such that MD2+MC2 is minimum is:

(MD)2 = x2+82 = x2+64
(MC)2 = (10-x)2 +(11)2 = (x-10)2+121
f(x) = (MD)2+(MC)2 = x2+64 +(x-10)2+(121)
Differentiate
f'(x) = 0
2x+2(x-10) = 0
4x = 20
⇒ x = 5
f’’(x) = 4 > 0
at x = 5 point of minima
Answer: 5
23. Let f : R → R be defined as

The value of λ for which f”(0) exists, is


If f’’(0) exists then
f’’(0+) = f’’(0–)
2λ = 10
⇒ λ = 5
Answer: 5
24. The angle of elevation of the top of a hill from a point on the horizontal plane passing through the foot of the hill is found to be 450. After walking a distance of 80 meters towards the top, up a slope inclined at an angle of 300 to the horizontal plane, the angle of elevation of the top of the hill becomes 750. Then the height of the hill (in meters) is:

x = 80 cos 300 = 40v3
y = 80 sin 300 = 40
In ΔADC, tan 450 = h/(x+z)
⇒ h = x+z
⇒h = 40v3+z ..(i)
In ΔEDF
tan 750 = (h-y)/z
2+v3 = (h-40)/z
⇒ z = (h-40)/(2+v3) ..(ii)
Put the value of z from (i)
h-40v3 = (h-40)/(2+v3)
h(1+v3) = 40(2v3+3-1)
h(1+v3) = 80(1+v3)
h = 80
Answer: 80
25. Set A has m elements and set B has n elements. If the total number of subsets of A is 112 more than the total number of subsets of B, then the value of m×n is
A and B are two sets having m, n element respectively
No. of subsets of A = 2m
No. of subsets of B = 2n
2m = 2n +112
2m -2n = 112
2n (2m-n-1) = 112
2n(2m-n-1) = 24 (23-1)
n = 4
m-n = 3
m-4 = 3
⇒ m = 7
m×n = 28
Answer: 28
Video Lessons – September 6 Shift 1 Maths


















Comments