The JEE Main 2022 June 27 – Shift 2 Maths Question Paper with Solutions are provided on this page. Revising the JEE Main 2022 question papers will definitely help students to take their preparation to the next level. The JEE Main 2022 June 27 – Shift 2 Maths Question Paper with Solutions can be used to evaluate their performance in the JEE Main 2022 exams. These solutions are easy to understand since they are given in a detailed manner. Check out the JEE Main 2022 June 27 – Shift 2 Maths answer keys below.
JEE Main 2022 June 27th Maths Shift 2 Question Paper and Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. The number of points of intersection of |z – (4 + 3i)| = 2 and |z| + |z – 4| = 6, z ∈ C, is
(A) 0
(B) 1
(C) 2
(D) 3
Answer (C)
Sol. C1 : |z – (4 + 3i)| = 2 and C2 : |z| + |z – 4| = 6, z ∈ C
C1: represents a circle with centre (4, 3) and radius 2 and C2 represents a ellipse with focii at (0, 0) and (4, 0) and length of major axis = 6, and length of semi-major axis 2√5 and (4, 2) lies inside the both C1 and C2 and (4, 3) lies outside the C2
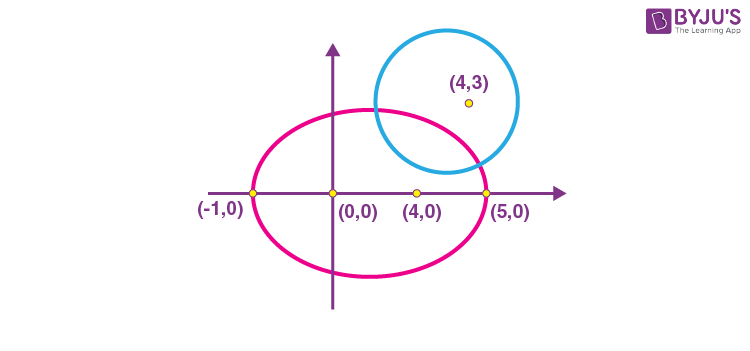
So, number of intersection points = 2
2. Let \(\begin{array}{l}f(x) = \begin{vmatrix}a & -1 & 0 \\ax & a & -1 \\ax^2 & ax & a \\\end{vmatrix},\end{array} \)
a ∈ R. Then the sum of the square of all the values of a, for which 2f′(10) –f′(5) + 100 = 0, is
(A) 117
(B) 106
(C) 125
(D) 136
Answer (C)
Sol.
\(\begin{array}{l}f(x) = \begin{vmatrix}a & -1 & 0 \\ax & a & -1 \\ax^2 & ax & a \\\end{vmatrix},\ a\in R\end{array} \)
f(x) = a(a2 + ax) + 1(a2x + ax2)
= a(x + a)2
f′(x) = 2a(x + a)
Now, 2f′(10) – f′(5) + 100 = 0
⇒ 2·2a(10 + a) – 2a(5 + a) + 100 = 0
⇒ 2a(a + 15) + 100 = 0
⇒ a2 + 15a + 50 = 0
⇒ a = –10, –5
∴ Sum of squares of values of a = 125.
3. Let for some real numbers α and β, a = α – iβ. If the system of equations 4ix + (1 + i) y = 0 and \(\begin{array}{l}8\left ( cos \frac{2\pi}{3} + i~sin\frac{2\pi}{3} \right )x + \overline{a} y = 0\end{array} \)
has more than one solution, then α/β is equal to
(A) -2 + √3
(B) 2 – √3
(C) 2 + √3
(D) -2 – √3
Answer (B)
Sol. Given a = α – iβ and
4ix + (1 + i)y = 0 …(i)
\(\begin{array}{l}8\left ( cos\frac{2\pi}{3} + isin\frac{2\pi}{3} \right )x + \overline{a} y = 0….(ii)\end{array} \)
By (i)
\(\begin{array}{l}\frac{x}{y} = \frac{-(1 + i)}{4i}…(iii)\end{array} \)
By (ii)
\(\begin{array}{l}\frac{x}{y} = \frac{-\overline{a}}{8\left ( \frac{-1}{2} + \frac{\sqrt{3}i}{2} \right )}….(iv)\end{array} \)
Now by (iii) and (iv)
\(\begin{array}{l}\frac{1+i}{4i} = \frac{\overline{a}}{4(-1+\sqrt{3}i)}\end{array} \)
\(\begin{array}{l}\Rightarrow \overline{a} = (\sqrt{3} – 1)+ (\sqrt{3} + 1)i\end{array} \)
\(\begin{array}{l}\Rightarrow \alpha + i\beta = (\sqrt{3} – 1) + (\sqrt{3} + 1) i\end{array} \)
\(\begin{array}{l}\therefore \frac{\alpha}{\beta} = \frac{\sqrt{3}- 1}{\sqrt{3} + 1} = 2 – \sqrt{3}\end{array} \)
4. Let A and B be two 3 × 3 matrices such that AB = I and |A| = ⅛. Then |adj (B adj(2A))| is equal to
(A) 16
(B) 32
(B) 64
(D) 128
Answer (C)
Sol. A and B are two matrices of order 3 × 3.
and AB = I,
\(\begin{array}{l}|A| =\frac{1}{8}\end{array} \)
Now, |A| |B| = 1
|B| = 8
∴ |adj(B(adj(2A))| = |B(adj(2A))|2
= |B|2|adj(2A)|2
= 26|2A|2×2
\(\begin{array}{l}=2^6.2^{12}.\frac{1}{2^{12}} = 64\end{array} \)
5. Let \(\begin{array}{l}S=2+\frac{6}{7}+\frac{12}{7^2}+\frac{20}{7^3}+\frac{30}{7^4}+…\end{array} \)
Then 4S is equal to
\(\begin{array}{l}(A)\ \left ( \frac{7}{3} \right )^2\end{array} \)
\(\begin{array}{l}(B)\ \left ( \frac{7^3}{3^2} \right )\end{array} \)
\(\begin{array}{l}(C)\ \left ( \frac{7}{3} \right )^3\end{array} \)
\(\begin{array}{l}(D)\ \left ( \frac{7^2}{3^3} \right )\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}S=2+\frac{6}{7}+\frac{12}{7^2}+\frac{20}{7^3}+\frac{30} {7^4}+… \ \dots(i) \end{array} \)
\(\begin{array}{l}\frac{1}{7}S=\frac{2}{7}+\frac{6}{7^2}+\frac{12}{7^3}+\frac{20}{7^4}+.. …(ii)\end{array} \)
(i) – (ii)
\(\begin{array}{l}\frac{6}{7}S=2+\frac{4}{7}+\frac{6}{7^2}+\frac{8}{7^3}+.. …(iii)\end{array} \)
\(\begin{array}{l}\frac{6}{7^2}S=\frac{2}{7}+\frac{4}{7^2}+\frac{6}{7^3}+… …(iv)\end{array} \)
(iii) – (iv)
\(\begin{array}{l}\left ( \frac{6}{7} \right )^2 S= 2+\frac{2}{7}+\frac{2}{7^2}+\frac{2}{7^3}+..\end{array} \)
\(\begin{array}{l}=2\left [ \frac{1}{1-\frac{1}{7}} \right ] = 2 \left ( \frac{7}{6} \right )\end{array} \)
\(\begin{array}{l}\therefore 4S=8\left ( \frac{7}{6} \right )^3 = \left ( \frac{7}{3} \right )^3\end{array} \)
6. If a1, a2, a3 ….. and b1, b2, b3 ….. are A.P., and a1 = 2, a10 = 3, a1b1 = 1 = a10b10, then a4b4 is equal to
\(\begin{array}{l}(A)\ \frac{35}{27}\end{array} \)
(B) 1
\(\begin{array}{l}(C)\ \frac{27}{28}\end{array} \)
\(\begin{array}{l}(D)\ \frac{28}{27}\end{array} \)
Answer (D)
Sol. a1, a2, a3 … are in A.P. (Let common difference is d1)
b1, b2, b3 … are in A.P. (Let common difference is d2)
and a1 = 2, a10 = 3, a1b1 = 1 = a10b10
∵ a1b1 = 1
\(\begin{array}{l}\therefore b_1 = \frac{1}{2}\end{array} \)
a10b10 = 1
\(\begin{array}{l}\therefore b_{10} = \frac{1}{3}\end{array} \)
Now,
\(\begin{array}{l}a_{10} = a_1 + 9d_1 \Rightarrow d_1 = \frac{1}{9} \end{array} \)
\(\begin{array}{l}b_{10} = b_1 + 9d_2 \Rightarrow d_2 = \frac{1}{9}\left [ \frac{1}{3}-\frac{1}{2} \right ]=-\frac{1}{54} \end{array} \)
Now,
\(\begin{array}{l}a_4 = 2 + \frac{3}{9} = \frac{7}{3} \end{array} \)
\(\begin{array}{l}b_4 = \frac{1}{2} – \frac{3}{54} = \frac{4}{9} \end{array} \)
\(\begin{array}{l}\therefore a_4b_4 = \frac{28}{27}\end{array} \)
7. If m and n respectively are the number of local maximum and local minimum points of the function \(\begin{array}{l}f(x) = \int_{0}^{x^2} \frac{t^2 – 5t + 4}{2 + e^t}dt,\end{array} \)
then the ordered pair (m, n) is equal to
(A) (3, 2)
(B) (2, 3)
(C) (2, 2)
(D) (3, 4)
Answer (B)
Sol.
\(\begin{array}{l}f(x) = \int_{0}^{x^2} \frac{t^2 – 5t + 4}{2 + e^t}dt\end{array} \)
\(\begin{array}{l}f’\left ( x \right )=2x\left ( \frac{x^4-5x^2+4}{2+ e^{x^2}} \right ) = 0\end{array} \)
\(\begin{array}{l}x=0, \textup{or} \left ( x^2 – 4 \right )\left ( x^2 – 1 \right ) = 0\end{array} \)
x = 0, x = ±2, ±1
Now,
\(\begin{array}{l}f'(x)=\frac{2x(x + 1)(x – 1) (x + 2) (x – 2)}{e^{x^2} + 2}\end{array} \)
changes sign from positive to negative at
x = –1, 1 So, number of local maximum points = 2
changes sign from negative to positive at
x = –2, 0, 2 So, number of local minimum points = 3
∴ m = 2, n = 3
8. Let f be a differentiable function in (0, π/2). \(\begin{array}{l}\text{If}\ \int_{cos x}^{1}t^2 f(t)dt = sin^3 x + cos x,\ \text{then}\ \frac{1}{\sqrt{3}} f’\left ( \frac{1}{\sqrt{3}} \right )\end{array} \)
is equal to
\(\begin{array}{l}(A)\ 6-9\sqrt{2}\end{array} \)
\(\begin{array}{l}(B)\ 6-\frac{9}{\sqrt{2}}\end{array} \)
\(\begin{array}{l}(C)\ \frac{9}{2}-6\sqrt{2}\end{array} \)
\(\begin{array}{l}(D)\ \frac{9}{\sqrt{2}}-6\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l}\int_{cos x}^{1}t^2f(t)dt = sin^3 x + cos ~x\end{array} \)
⇒ sin x cos2 x f(cos x) = 3 sin2 x cos x – sin x
⇒ f(cos x) = 3 tan x – sec2 x
⇒ f′(cos x) . (– sin x) = 3 sec2 x – 2 sec2 x tan x
Put
\(\begin{array}{l}cos x=\frac{1}{\sqrt{3}},\end{array} \)
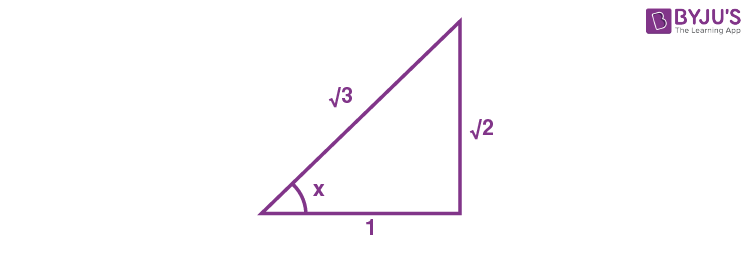
\(\begin{array}{l}\therefore f’\left ( \frac{1}{\sqrt{3}}\right )\left ( -\frac{\sqrt{2}}{\sqrt{3}} \right )=9-6\sqrt{2}\end{array} \)
\(\begin{array}{l}\frac{1}{\sqrt{3}}f’\left ( \frac{1}{\sqrt{3}} \right ) = 6 – \frac{9}{\sqrt{2}}\end{array} \)
9. The integral \(\begin{array}{l}\int_{0}^{1} \frac{1}{7^{\left [ \frac{1}{x} \right ]}}dx\end{array} \)
where [⋅] denotes the greatest integer function, is equal to
\(\begin{array}{l}(A)\ 1+6log_e\left (\frac{6}{7} \right )\end{array} \)
\(\begin{array}{l}(B)\ 1- 6log_e\left (\frac{6}{7} \right )\end{array} \)
\(\begin{array}{l}(C)\ log_e\left (\frac{7}{6} \right )\end{array} \)
\(\begin{array}{l}(D)\ 1 -7log_e\left (\frac{6}{7} \right )\end{array} \)
Answer (A)
Sol.
\(\begin{array}{l}\int_{0}^{1}\frac{1}{7^{\left [ \frac{1}{x} \right ]}}dx, \textup{let} \frac{1}{x} = t\end{array} \)
\(\begin{array}{l}\frac{-1}{x^2}dx = dt\end{array} \)
\(\begin{array}{l}=\int_{\infty}^{1} \frac{1}{-t^2 7^{[t]}}dt = \int_{1}^{\infty} \frac{1}{t^2 7^{[t]}}dt \end{array} \)
\(\begin{array}{l}=\int_{1}^{2} \frac{1}{7t^2}dt + \int_{2}^{3} \frac{1}{7^2 t^2 }dt+… \end{array} \)
\(\begin{array}{l}=\frac{1}{7} \left [ -\frac{1}{t} \right ]^2_1 + \frac{1}{7^2} \left [ \frac{-1}{t} \right ]^3_2 + \frac{1}{7^3}\left [ -\frac{1}{t} \right ]^3_2 +…\end{array} \)
\(\begin{array}{l}=\sum_{n=1}^{\infty} \frac{1}{7_n}\left ( \frac{1}{n}-\frac{1}{n+1} \right )\end{array} \)
\(\begin{array}{l}=\sum_{n=1}^{\infty} \frac{\left ( \frac{1}{7} \right )^n}{n}-7 \sum_{n=1}^{\infty} \frac{\left ( \frac{1}{7} \right )^{n+1}}{n+1}\end{array} \)
\(\begin{array}{l}=-\textup{log} \left ( 1-\frac{1}{7} \right )+7\textup{log}\left ( 1- \frac{1}{7} \right )+1\end{array} \)
\(\begin{array}{l}=1 + 6 \textup{log} \frac{6}{7}\end{array} \)
10. If the solution curve of the differential equation \(\begin{array}{l}\left ( \left ( tan^{-1}y \right )-x \right )dy = \left ( 1+ y^2 \right )dx\end{array} \)
passes through the point (1, 0), then the abscissa of the point on the curve whose ordinate is tan(1), is
(A) 2e
(B) 2/e
(C) 2
(D) 1/e
Answer (B)
Sol.
\(\begin{array}{l}\left ( \left ( tan^{-1}y \right )-x \right )dy = \left ( 1+ y^2 \right )dx\end{array} \)
\(\begin{array}{l}\frac{dx}{dy}+\frac{x}{1+y^2} = \frac{tan^{-1}y}{1+y^2}\end{array} \)
\(\begin{array}{l}I.F. = e^{\int_{\frac{1}{1+y^2}dy}}=e^{tan^{-1}y}\end{array} \)
∴ Solution
\(\begin{array}{l}x.e^{tan^{-1}y} \int_{}^{}\frac{e^{tan^{-1}y} ~{tan^{-1}}y}{1+y^2} dy \end{array} \)
Let
\(\begin{array}{l}e^{tan^{-1}y} = t\end{array} \)
\(\begin{array}{l}\frac{e^{tan^{-1} y} }{1+y^2} = dt\end{array} \)
\(\begin{array}{l}= xe^{tan^{-1}y} \int \textup{ln}~ td~t= t ~\textup{ln}~t – t + c\end{array} \)
\(\begin{array}{l}= xe^{tan^{-1}y} = e^{tan^{-1}y} tan^{-1} y – e^{tan^{-1}y}+c…(i)\end{array} \)
∵ It passes through (1, 0) ⇒ c = 2
Now put y = tan1, then
ex = e – e + 2
\(\begin{array}{l}\Rightarrow x=\frac{2}{e}\end{array} \)
11. If the equation of the parabola, whose vertex is at (5, 4) and the directrix is 3x + y – 29 = 0, is x2 + ay2 + bxy + cx + dy + k = 0, then a + b + c + d + k is equal to
(A) 575
(B) –575
(C) 576
(D) –576
Answer (D)
Sol. Given vertex is (5, 4) and directrix 3x + y – 29 = 0
Let foot of perpendicular of (5, 4) on directrix be (x1, y1).
\(\begin{array}{l}\frac{x_{1}-5}{3}=\frac{y_{1}-4}{1}=\frac{-(-10)}{10}\end{array} \)
∴ (x1, y1) = (8, 5)
So, focus of parabola will be S = (2, 3)
Let P(x, y) be any point on parabola, then
\(\begin{array}{l}(x-2)^{2}+(y-3)^{2}=\frac{(3 x+y-29)^{2}}{10}\end{array} \)
\(\begin{array}{l}\Rightarrow 10\left(x^{2}+y^{2}-4 x-6 y+13\right)=9 x^{2}+y^{2}+841+6 x y-58 y-174x\end{array} \)
\(\begin{array}{l}\Rightarrow x^{2}+9 y^{2}-6 x y+134 x-2 y-711 = 0\end{array} \)
and given parabola
\(\begin{array}{l}x^{2}+a y^{2}+b x y+c x+d y+k = 0\end{array} \)
∴ a = 9, b = –6, c = 134, d = –2, k = –711
∴ a + b + c + d + k = –576
12. The set of values of k, for which the circle C : 4x2 + 4y2 – 12x + 8y + k = 0 lies inside the fourth quadrant and the point (1, -1/3) lies on or inside the circle C, is
(A) An empty set
\(\begin{array}{l}(B)\ \left(6, \frac{65}{9}\right]\end{array} \)
\(\begin{array}{l}(C)\ \left( \frac{80}{9},10\right]\end{array} \)
\(\begin{array}{l}(D)\ \left(9, \frac{92}{9}\right]\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l}C : 4 x^{2}+4 y^{2}-12 x+8 y+k=0\end{array} \)
\(\begin{array}{l}\because \left(1,-\frac{1}{3}\right)\end{array} \)
lies on or inside the C then \(\begin{array}{l}4+\frac{4}{9}-12-\frac{8}{3}+k \leq 0\end{array} \)
\(\begin{array}{l}\Rightarrow k \leq \frac{92}{9}\end{array} \)
Now, circle lies in 4th quadrant centre
\(\begin{array}{l}\equiv\left(\frac{3}{2},-1\right)\end{array} \)
\(\begin{array}{l}\therefore r<1 \Rightarrow \sqrt{\frac{9}{4}+1-\frac{k}{4}}<1\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{13}{4}-\frac{k}{4}<1\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{k}{4}>\frac{9}{4}\end{array} \)
⇒k > 9
\(\begin{array}{l}\therefore k \in\left(9, \frac{92}{9}\right)\end{array} \)
13. Let the foot of the perpendicular from the point (1, 2, 4) on the line \(\begin{array}{l}\frac{x+2}{4}=\frac{y-1}{2}=\frac{z+1}{3}\end{array} \)
be P, Then the distance of P from the plane 3x + 4y + 12z + 23 = 0 is
(A) 5
\(\begin{array}{l}(B)\ \frac{50}{13}\end{array} \)
(C) 4
\(\begin{array}{l}(D)\ \frac{63}{13}\end{array} \)
Answer (A)
Sol.
\(\begin{array}{l}L: \frac{x+2}{4}=\frac{y-1}{2}=\frac{z+1}{3}=t\end{array} \)
Let
\(\begin{array}{l}P=(4 t-2,2 t+1,3 t-1)\end{array} \)
∵ P is the foot of perpendicular of (1, 2, 4)
∴ 4(4t – 3) + 2(2t – 1) + 3(3t – 5) = 0
\(\begin{array}{l}\Rightarrow 29 t=29 \Rightarrow t=1\end{array} \)
∴ P = (2, 3, 2)
Now, distance of P from the plane
3x + 4y + 12z + 23 = 0, is
\(\begin{array}{l}\left|\frac{6+12+24+23}{\sqrt{9+16+144}}\right|=\frac{65}{13}=5\end{array} \)
14. The shortest distance between the lines \(\begin{array}{l}\frac{x-3}{2}=\frac{y-2}{3}=\frac{z-1}{-1}\end{array} \)
and \(\begin{array}{l}\frac{x+3}{2}=\frac{y-6}{1}=\frac{z-5}{3},\ \text{is}\end{array} \)
\(\begin{array}{l}(A)\ \frac{18}{\sqrt{5}}\end{array} \)
\(\begin{array}{l}(B)\ \frac{22}{3 \sqrt{5}}\end{array} \)
\(\begin{array}{l}(C)\ \frac{46}{3 \sqrt{5}}\end{array} \)
\(\begin{array}{l}(D)\ 6 \sqrt{3}\end{array} \)
Answer (A)
Sol.
\(\begin{array}{l}L_{1}: \frac{x-3}{2}=\frac{y-2}{3}=\frac{z-1}{-1}\end{array} \)
\(\begin{array}{l}L_{2}: \frac{x+3}{2}=\frac{y-6}{1}=\frac{z-5}{3}\end{array} \)
Now,
\(\begin{array}{l}\vec{p} \times \vec{q}=\left|\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k} \\ 2 & 3 & -1 \\ 2 & 1 & 3\end{array}\right|=10 \hat{i}-8 \hat{j}-4 \hat{k}\end{array} \)
and
\(\begin{array}{l}\vec{a}_{2}-\vec{a}_{1}=6 \hat{i}-4 \hat{j}-4 \hat{k}\end{array} \)
\(\begin{array}{l}\therefore S.D =\left|\frac{60+32+16}{\sqrt{100+64+16}}\right|=\frac{108}{\sqrt{180}}=\frac{18}{\sqrt{5}}\end{array} \)
15. Let \(\begin{array}{l}\vec{a}\ \text{and}\ \vec{b}\end{array} \)
be the vectors along the diagonals of a parallelogram having area 2√2. Let the angle between \(\begin{array}{l}\vec{a}\ \text{and}\ \vec{b}\ \text{be acute,}\ |\vec{a}|=1,\ \text{and}\ |\vec{a} \cdot \vec{b}|=|\vec{a} \times \vec{b}|\end{array} \)
\(\begin{array}{l}\text{If}\ \vec{c}=2 \sqrt{2}(\vec{a} \times \vec{b})-2 \vec{b}\ \text{then an angle between}\ \vec{b}\ \text{and}\ \vec{c}\ \text{is}\end{array} \)
\(\begin{array}{l}(A)\ \frac{\pi}{4}\end{array} \)
\(\begin{array}{l}(B)\ -\frac{\pi}{4}\end{array} \)
\(\begin{array}{l}(C)\ \frac{5\pi}{6}\end{array} \)
\(\begin{array}{l}(D)\ \frac{3\pi}{4}\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l}\because \vec{a}\ and\ \vec{b}\end{array} \)
be the vectors along the diagonals of a parallelogram having area 2√2.
\(\begin{array}{l}\therefore \frac{1}{2}|\vec{a} \times \vec{b}|=2 \sqrt{2}\end{array} \)
\(\begin{array}{l}|\vec{a}||\vec{b}| \sin \theta=4 \sqrt{2}\end{array} \)
\(\begin{array}{l}\Rightarrow |\vec{b}| \sin \theta=4 \sqrt{2}…(i)\end{array} \)
and
\(\begin{array}{l}|\vec{a} \cdot \vec{b}|=|\vec{a} \times \vec{b}|\end{array} \)
\(\begin{array}{l}|\vec{a}||\vec{b}| \cos \theta=|\vec{a}||\vec{b}| \sin \theta\end{array} \)
\(\begin{array}{l}\Rightarrow \tan \theta=1 \quad \therefore \theta=\frac{\pi}{4}\end{array} \)
By (i)
\(\begin{array}{l}|\vec{b}|=8\end{array} \)
Now
\(\begin{array}{l}\vec{c}=2 \sqrt{2}(\vec{a} \times \vec{b})-2 \vec{b}\end{array} \)
\(\begin{array}{l}\Rightarrow \vec{c} \cdot \vec{b}=-2|\vec{b}|^{2}=-128…(ii)\end{array} \)
and
\(\begin{array}{l}\vec{c} \cdot \vec{c}=8|\vec{a} \times \vec{b}|^{2}+4|\vec{b}|^{2}\end{array} \)
\(\begin{array}{l}\Rightarrow |\vec{c}|^{2}=8.32+4.64\end{array} \)
\(\begin{array}{l}\Rightarrow |\vec{c}|=16 \sqrt{2}…(iii)\end{array} \)
From (ii) and (iii)
\(\begin{array}{l}|\vec{c}||\vec{b}| \cos \alpha=-128\end{array} \)
\(\begin{array}{l}\Rightarrow \cos \alpha=\frac{-1}{\sqrt{2}}\end{array} \)
\(\begin{array}{l}\alpha=\frac{3 \pi}{4}\end{array} \)
16. The mean and variance of the data 4, 5, 6, 6, 7, 8, x, y, where x < y, are 6 and 9/4, respectively. Then x4 + y2 is equal to
(A) 162
(B) 320
(C) 674
(D) 420
Answer (B)
Sol. Mean
\(\begin{array}{l}=\frac{4+5+6+6+7+8+x+y}{8} = 6\end{array} \)
∴ x + y = 12 …(i)
And variance
\(\begin{array}{l}=\frac{2^{2}+1^{2}+0^{2}+0^{2}+1^{2}+2^{2}+(x-6)^{2}+(y-6)^{2}}{8}\end{array} \)
\(\begin{array}{l}=\frac{9}{4}\end{array} \)
∴ (x – 6)2 + (y – 6)2 = 8 …(ii)
From (i) and (ii)
x = 4 and y = 8
∴ x4 +y2 = 320
17. If a point A(x, y) lies in the region bounded by the y-axis, straight lines 2y + x = 6 and 5x – 6y = 30, then the probability that y < 1 is
\(\begin{array}{l}(A)\ \frac{1}{6}\end{array} \)
\(\begin{array}{l}(B)\ \frac{5}{6}\end{array} \)
\(\begin{array}{l}(C)\ \frac{2}{3}\end{array} \)
\(\begin{array}{l}(D)\ \frac{6}{7}\end{array} \)
Answer (B)
Sol. The required probability
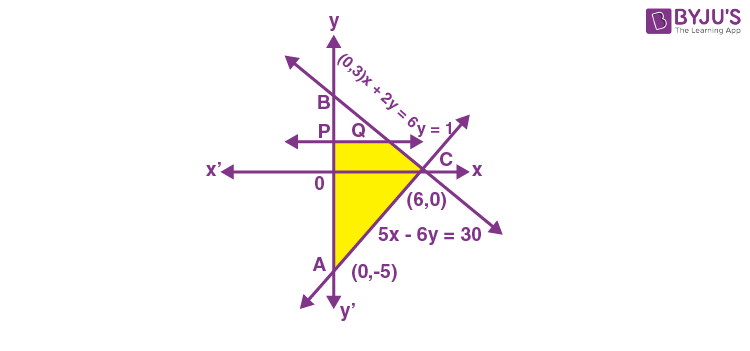
\(\begin{array}{l}=\frac{\text { Area of Region } P Q C A P}{\text { Area of Region } A B C A}\end{array} \)
\(\begin{array}{l}=\frac{\frac{1}{2} \times 8 \times 6-\frac{1}{2} \times 2 \times 4}{\frac{1}{2} \times 8 \times 6}\end{array} \)
\(\begin{array}{l}=\frac{5}{6}\end{array} \)
18. The value of \(\begin{array}{l}\cot \left(\sum_{n=1}^{50} \tan ^{-1}\left(\frac{1}{1+n+n^{2}}\right)\right)\end{array} \)
is
\(\begin{array}{l}(A) \frac{26}{25}\end{array} \)
\(\begin{array}{l}(B) \frac{25}{26}\end{array} \)
\(\begin{array}{l}(C)\ \frac{50}{51}\end{array} \)
\(\begin{array}{l}(D)\ \frac{52}{51}\end{array} \)
Answer (A)
Sol.
\(\begin{array}{l}\cot \left(\sum_{n=1}^{50} \tan ^{-1}\left(\frac{1}{1+n+n^{2}}\right)\right)\end{array} \)
\(\begin{array}{l}=\cot \left(\sum_{n=1}^{50} \tan ^{-1}\left(\frac{(n+1)-n}{1+(n+1) n}\right)\right)\end{array} \)
\(\begin{array}{l}=\cot \left(\sum_{n=1}^{50}\left(\tan ^{-1}(n+1)-\tan ^{-1} n\right)\right)\end{array} \)
\(\begin{array}{l}=\cot \left(\tan ^{-1} 51-\tan ^{-1} 1\right)\end{array} \)
\(\begin{array}{l}=\cot \left(\tan ^{-1}\left(\frac{51-1}{1+51}\right)\right)\end{array} \)
\(\begin{array}{l}=\cot \left(\cot ^{-1}\left(\frac{52}{50}\right)\right)\end{array} \)
\(\begin{array}{l}=\frac{26}{25}\end{array} \)
19. α = sin 36º is a root of which of the following equation?
(A) 16x4 – 10x2 – 5 = 0
(B) 16x4 + 20x2 – 5 = 0
(C) 16x4 – 20x2 + 5 = 0
(D) 16x4 – 10x2 + 5 = 0
Answer (C)
Sol. α = sin36° = x(say)
\(\begin{array}{l}\therefore x=\frac{\sqrt{10-2 \sqrt{5}}}{4}\end{array} \)
⇒ 16x2 = 10 – 2√5
⇒ (8x2 – 5)2 = 5
⇒ 16x4 – 80x2 + 20 = 0
∴ 4x4 – 20x2 + 5 = 0
20. Which of the following statement is a tautology?
(A) ((~ q) ∧ p) ∧ q
(B) ((~ q) ∧ p) ∧ (p ∧ (~ p))
(C) ((~ q) ∧ p) ∨ (p ∨ (~p))
(D) (p ∧ q) ∧ (~ (p ∧ q))
Answer (C)
Sol. ∵ ((~ q) ∧ p) ∨ (p ∨ (~ p))
= (~ q ∧ p) ∨ t (t is tautology)
≡ t
∴ option (C) is correct.
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, –00.33, –00.30, 30.27, –27.30) using the mouse and the on-screen virtual numeric keypad in the place designated to enter the answer.
1. Let S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Define f : S → S as
\(\begin{array}{l}f(n)=\left\{\begin{array}{ll}2 n & , \text { if } n=1,2,3,4,5 \\ 2 n-11, & \text { if } n=6,7,8,9,10\end{array} .\right.\end{array} \)
Let g : S → S be a function such that
\(\begin{array}{l}f o g(n)= \begin{cases}n+1 & , \text { if } n \text { is odd } \\ n-1 & , \text { if } n \text { is even }\end{cases}\end{array} \)
Then g(10) (g(1) + g(2) + g(3) + g(4) + g(5)) is equal to __________.
Answer (190)
Sol.
\(\begin{array}{l}\because f(n) = \begin{cases}2 n & , n=1,2,3,4,5 \\ 2 n-11, & n=6,7,8,9,10\end{cases}\end{array} \)
∴ f(1) = 2, f(2) = 4, … , f(5) = 10
and f(6) = 1, f(7) = 3, f(8) = 5, … , f(10) = 9
Now,
\(\begin{array}{l}f(g(n))= \begin{cases}n+1 & \text { if } n \text { is odd } \\ n-1, & \text { if } n \text { is even }\end{cases}\end{array} \)
∴ f(g(10)) = 9 ⇒ g(10) = 10
f(g(1)) = 2 ⇒ g(1) = 1
f(g(2)) = 1 ⇒ g(2) = 6
f(g(3)) = 4 ⇒ g(3) = 2
f(g(4)) = 3 ⇒ g(4) = 7
f(g(5)) = 6 ⇒ g(5) = 3
∴ g(10) (g(1) + g(2) + g(3) + g(4) + g(5)) = 190
2. Let α, β be the roots of the equation x2 – 4λx + 5 = 0 and α, γ be the roots of the equation \(\begin{array}{l}x^{2}-(3 \sqrt{2}+2 \sqrt{3}) x+7+3 \lambda \sqrt{3}=0,\end{array} \)
λ > 0. If β + γ = 3√2, then (α + 2β + γ)2 is equal to _______.
Answer (98)
Sol.
∵ α, β are roots of x2 – 4λx + 5 = 0
∴ α + β = 4λ and αβ = 5
Also, α, γ are roots of
\(\begin{array}{l}x^{2}-(3 \sqrt{2}+2 \sqrt{3}) x+7+3 \sqrt{3} \lambda=0, \lambda>0\end{array} \)
\(\begin{array}{l}\therefore \alpha + \gamma = 3\sqrt{2}+2 \sqrt{3}, \quad \alpha \gamma=7+3 \sqrt{3} \lambda\end{array} \)
∵ α is common root
∴ α2 – 4λ α + 5 = 0 …(i)
and
\(\begin{array}{l}\alpha^{2}-(3 \sqrt{2}+2 \sqrt{3}) \alpha+7+3 \sqrt{3} \lambda=0…(ii)\end{array} \)
From (i) – (ii): we get
\(\begin{array}{l}\alpha=\frac{2+3 \sqrt{3} \lambda}{3 \sqrt{2}+2 \sqrt{3}-4 \lambda}\end{array} \)
∵ β + γ = 3√2
\(\begin{array}{l}\therefore 4 \lambda+3 \sqrt{2}+2 \sqrt{3}-2 \alpha=3 \sqrt{2}\end{array} \)
\(\begin{array}{l}\Rightarrow 3 \sqrt{2}=4 \lambda+3 \sqrt{2}+2 \sqrt{3}-\frac{4+6 \sqrt{3} \lambda}{3 \sqrt{2}+2 \sqrt{3}-4 \lambda}\end{array} \)
\(\begin{array}{l}\Rightarrow 8 \lambda^{2}+3(\sqrt{3}-2 \sqrt{2}) \lambda-4-3 \sqrt{6}=0\end{array} \)
\(\begin{array}{l}\therefore \lambda=\frac{6 \sqrt{2}-3 \sqrt{3} \pm \sqrt{9(11-4 \sqrt{6})+32(4+3 \sqrt{6})}}{16}\end{array} \)
\(\begin{array}{l}\therefore \lambda=\sqrt{2}\end{array} \)
∴ (α + 2β + γ)2 = (α + β + β + γ)2
\(\begin{array}{l}=(4 \sqrt{2}+3 \sqrt{2})^{2}\end{array} \)
\(\begin{array}{l}=(7 \sqrt{2})^{2}\end{array} \)
= 98
3. Let A be a matrix of order 2 × 2, whose entries are from the set {0, 1, 3, 4, 5}. If the sum of all the entries of A is a prime number p, 2 < p < 8, then the number of such matrices A is ___________.
Answer (180)
Sol. ∵ Sum of all entries of matrix A must be prime p such that 2 < p < 8 then sum of entries may be 3, 5 or 7.
If sum is 3 then possible entries are (0, 0, 0, 3), (0, 0, 1, 2) or (0, 1, 1, 1).
∴ Total number of matrices = 4 + 4 + 12 = 20
If sum of 5 then possible entries are
(0, 0, 0, 5), (0, 0, 1, 4), (0, 0, 2, 3), (0, 1, 1, 3),
(0, 1, 2, 2) and (1, 1, 1, 2).
∴ Total number of matrices = 4 + 12 + 12 + 12 + 12 + 4 = 56
If sum is 7 then possible entries are
(0, 0, 2, 5), (0, 0, 3, 4), (0, 1, 1, 5), (0, 3, 3, 1), (0, 2, 2, 3), (1, 1, 1, 4), (1, 2, 2, 2), (1, 1, 2, 3) and (0, 1, 2, 4)
Total number of matrices with sum 7 = 104
∴ Total number of required matrices
= 20 + 56 + 104
= 180
4. If the sum of the coefficients of all the positive powers of x, in the Binomial expansion of \(\begin{array}{l}\left(x^{n}+\frac{2}{x^{5}}\right)^{7}\end{array} \)
is 939, then the sum of all the possible integral values of n is ____________.
Answer (57)
Sol.
\(\begin{array}{l}\begin{aligned}\left(x^{n}+\frac{2}{x^{5}}\right)^{7} &=\sum_{r=0}^{7}{ }^{7} C_{r}\left(x^{n}\right)^{7-r} \cdot\left(\frac{2}{x^{5}}\right)^{r} \\&=\sum_{r=0}^{7}{ }^{7} C_{r} \cdot 2^{r} \cdot x^{7 n-n r-5 r}\end{aligned}\end{array} \)
\(\begin{array}{l}\quad{ }^{7} C_{0} \cdot 2^{0}+{ }^{7} C_{1} \cdot 2^{1}+{ }^{7} C_{2} \cdot 2^{2}+{ }^{7} C_{3} \cdot 2^{3}+{ }^{7} C_{4} \cdot 2^{4}\end{array} \)
= 939
∴ r = 4
∵ 7n – nr – 5r = 0
and r = 4 then
\(\begin{array}{l}n>\frac{20}{3}\end{array} \)
and r should not be 5
\(\begin{array}{l}\therefore n<\frac{25}{2}\end{array} \)
∴ Possible values of n are 7, 8, 9, 10, 11, 12
∴ Sum of integral value of n = 57
5. Let [t] denote the greatest integer ≤ t and {t} denote the fractional part of t. The integral value of α for which the left hand limit of the function
\(\begin{array}{l}f(x) =[1+x]+\frac{\alpha^{2[x]+\{x\}}+[x]-1}{2[x]+\{x\}} \text { at } x=0 \text { is equal to }\ \alpha-\frac{4}{3}, \text { is }\end{array} \)
Answer (3)
\(\begin{array}{l}f(x) =[1+x]+\frac{\alpha^{2[x]+\{x\}}+[x]-1}{2[x]+\{x\}}\end{array} \)
\(\begin{array}{l}\lim _{x \rightarrow 0^{-}} f(x)=\alpha-\frac{4}{3}\end{array} \)
\(\begin{array}{l}\Rightarrow \lim _{x \rightarrow 0^{-}} 1+[x]+\frac{\alpha^{x+[x]}+[x]-1}{x+[x]}=\alpha-\frac{4}{3}\end{array} \)
\(\begin{array}{l}\Rightarrow \lim _{h \rightarrow 0^{-}} 1-1+\frac{\alpha^{-h-1}-1-1}{-h-1}=\alpha-\frac{4}{3}\end{array} \)
\(\begin{array}{l}\therefore \frac{\alpha^{-1}-2}{-1}=\alpha-\frac{4}{3}\end{array} \)
⇒ 3α2 – 10α + 3 = 0
∴ α = 3 or 1/3
∵ α in integer, hence α = 3
6. If y(x) = (xx)x, x > 0, then \(\begin{array}{l}\frac{d^{2} x}{d y^{2}}+20\end{array} \)
at x = 1 is equal to __________.
Answer (16)
Sol.
\(\begin{array}{l}\because y(x)=\left(x^x\right)^x\end{array} \)
\(\begin{array}{l}\therefore y=x^{x^{2}}\end{array} \)
\(\begin{array}{l}\therefore \quad \frac{d y}{d x}=x^{2} \cdot x^{x^{2}-1}+x^{x^{2}} \ln x \cdot 2 x\end{array} \)
\(\begin{array}{l}\therefore \frac{d x}{d y}=\frac{1}{x^{x^{2}+1}(1+2 \ln x)}….(i)\end{array} \)
Now,
\(\begin{array}{l}\frac{d^{2} x}{d x}=\frac{d}{d x}\left(\left(x^{x^{2}+1}(1+2 \ln x)\right)^{-1}\right) \cdot \frac{d x}{d y}\end{array} \)
\(\begin{array}{l}=\frac{-x\left(x^{x^{2}+1}(1+2 \ln x)\right)^{-2} \cdot x^{x^{2}}(1+2 \ln x)\left(x^{2}+2 x^{2} \ln x+3\right)}{x^{x^{2}}(1+2 \ln x)}\end{array} \)
\(\begin{array}{l}=\frac{-x^{x^{2}}(1+2 \ln x)\left(x^{2}+3+2 x^{2} \ln x\right)}{\left(x^{x^{2}}(1+2 \ln x)\right)^{3}}\end{array} \)
\(\begin{array}{l}\frac{d^{2} x}{d y^{2}(\text { at } x=1)}=-4\end{array} \)
\(\begin{array}{l}\therefore \frac{d^{2} x}{d y^{2}(\text { at } x=1)}+20=16\end{array} \)
7. If the area of the region \(\begin{array}{l}\left\{(x, y): x^{\frac{2}{3}}+y^{\frac{2}{3}} \leq 1, x+y \geq 0, y \geq 0\right\}\end{array} \)
is A, then (256 A)/π is equal to _______.
Answer (36)
Sol.

∴ Area of shaded region
\(\begin{array}{l}=\int_{-\left(\frac{1}{2}\right)^{\frac{3}{2}}}^{0}\left ( \left(1-x^{\frac{2}{3}}\right)^{\frac{3}{2}}+x \right ) d x+ \int_{0}^{1}\left(1-x^{\frac{2}{3}}\right)^{\frac{3}{2}} dx\end{array} \)
\(\begin{array}{l}=\int_{-\left(\frac{1}{2}\right)^{\frac{3}{2}}}^{0}\left(1-x^{\frac{2}{3}}\right)^{\frac{3}{2}} d x+\int_{-\left(\frac{1}{2}\right)^{\frac{3}{2}}}^{0} x d x\end{array} \)
Let x = sin3θ
∴ dx = 3sin2 θ cos θdθ
\(\begin{array}{l}=\int_{-\frac{\pi}{4}}^{\frac{\pi}{2}} 3 \sin ^{2} \theta \cos ^{4} \theta d \theta+\left(0-\frac{1}{16}\right)\end{array} \)
\(\begin{array}{l}=\frac{9 \pi}{64}+\frac{1}{16}-\frac{1}{16}=\frac{36 \pi}{256}=A\end{array} \)
\(\begin{array}{l}\therefore \frac{256 A}{\pi}=36\end{array} \)
8. Let y = y(x) be the solution of the differential equation \(\begin{array}{l}\left(1-x^{2}\right) d y=\left(x y+\left(x^{3}+2\right) \sqrt{1-x^{2}}\right) d x\end{array} \)
–1 < x < 1, and y(0) = 0. \(\begin{array}{l}\text{If}\ \int_{\frac{-1}{2}}^{\frac{1}{2}} \sqrt{1-x^{2}} y(x) d x=k\ \text{then}\ k^{-1}\ \text{is equal to}——–.\end{array} \)
Answer (320)
Sol.
\(\begin{array}{l}\left(1-x^{2}\right) d y=\left(x y+\left(x^{3}+2\right) \sqrt{1-x^{2}}\right) d x\end{array} \)
\(\begin{array}{l}\therefore \frac{d y}{d x}-\frac{x}{1-x^{2}} y=\frac{x^{3}+3}{\sqrt{1-x^{2}}}\end{array} \)
\(\begin{array}{l}\therefore I.F. =e^{\int-\frac{x}{1-x^{2}} d x}=\sqrt{1-x^{2}}\end{array} \)
Solution is
\(\begin{array}{l}y \cdot \sqrt{1-x^{2}}=\int\left(x^{3}+3\right) d x\end{array} \)
\(\begin{array}{l}y \cdot \sqrt{1-x^{2}}=\frac{x^{4}}{4}+3 x+c\end{array} \)
\(\begin{array}{l}\because y(0)=0 \Rightarrow c=0\end{array} \)
\(\begin{array}{l}\therefore y(x)=\frac{x^{4}+12 x}{4 \sqrt{1-x^{2}}}\end{array} \)
\(\begin{array}{l}\therefore \int_{\frac{-1}{2}}^{\frac{1}{2}} \sqrt{1-x^{2}}~~ y(x) d x=\int_{\frac{-1}{2}}^{\frac{1}{2}}\left(\frac{x^{4}+12 x}{4}\right) d x\end{array} \)
\(\begin{array}{l}=\int_{0}^{\frac{1}{2}} \frac{x^{4}}{2} d x\end{array} \)
\(\begin{array}{l}\therefore k=\frac{1}{320}\end{array} \)
\(\begin{array}{l}\therefore k^{-1} = 320\end{array} \)
9. Let a circle C of radius 5 lie below the x-axis. The line L1 : 4x + 3y + 2 = 0 passes through the centre P of the circle C and intersects the line L2 : 3x – 4y – 11 = 0 at Q. The line L2 touches C at the point Q. Then the distance of P from the line 5x – 12y + 51 = 0 is _____.
Answer (11)
Sol.
\(\begin{array}{l}L_{1}: 4 x+3 y+2=0\end{array} \)
\(\begin{array}{l}L_{2}: 3 x-4 y-11=0\end{array} \)
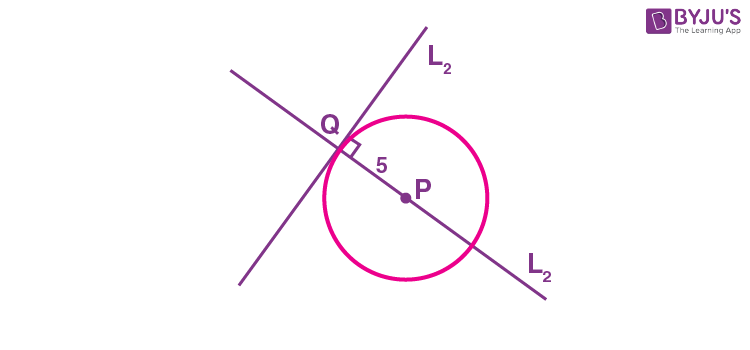
Since circle C touches the line L2 at Q intersection point Q of L1 and L2, is (1, –2)
∵ P lies of L1
\(\begin{array}{l}\therefore P\left(x,-\frac{1}{3}(2+4 x)\right)\end{array} \)
Now,
\(\begin{array}{l}P Q=5 \Rightarrow(x-1)^{2}+\left(\frac{4 x+2}{3}-2\right)^{2}=25\end{array} \)
\(\begin{array}{l}\Rightarrow(x-1)^{2}\left[1+\frac{16}{9}\right]=25\end{array} \)
⇒ (x – 1)2 = 9
⇒ x = 4, –2
∵ The circle lies below the x-axis.
y = –6
P(4, –6)
Now distance of P from 5x – 12y + 51 = 0
\(\begin{array}{l}=\left|\frac{20+72+51}{13}\right|=\frac{143}{13}=11\end{array} \)
10. Let S = {E1, E2, ……………., E8} be a sample space of a random experiment such that \(\begin{array}{l}P\left(E_{n}\right)=\frac{n}{36}\end{array} \)
for every n = 1, 2, ………, 8. Then the number of elements in the set \(\begin{array}{l}\left\{A \subseteq S: P(A) \geq \frac{4}{5}\right\}\end{array} \)
is _________ .
Answer (19)
Sol. Here P(En) = n/36 for n = 1, 2, 3, ………, 8
Here,
\(\begin{array}{l}P(A)=\frac{\text { Any possible sum of }(1,2,3, \ldots, 8)(=a \text { say })}{36}\end{array} \)
\(\begin{array}{l}\because \frac{a}{36} \geq \frac{4}{5}\end{array} \)
∴ a ≥ 29
If one of the number from {1, 2, …., 8} is left then total a ≥ 29 by 3 ways.
Similarly by leaving terms more 2 or 3 we get 16 more combinations.
∴ Total number of different set A possible is 16 + 3
= 19
JEE Main 2022 June 27th Shift 2 Paper with Solutions
JEE Main 2022 June 27 Shift 2 Question Paper – Physics Solutions
JEE Main 2022 June 27 Shift 2 Question Paper – Chemistry Solutions
JEE Main 2022 June 27 Shift 2 Question Paper – Maths Solutions
Frequently Asked Questions – FAQs
Q1
Is there a negative marking in section A of the JEE Main 2022 June 27 Shift 2 Maths question paper?
Yes. There is a negative marking in section A of the JEE Main 2022 June 27 Shift 2 Maths question paper. 1 mark will be deducted for every incorrect answer.
Q2
How was the JEE Main 2022 Shift 2 June 27 Maths question paper?
The JEE Main 2022 Shift 2 June 27 Maths question paper was easy to moderate difficulty. It had 9 easy questions, 7 medium questions and 1 difficult question as per the memory-based question paper.
Q3
Is there a choice in section A of the JEE Main 2022 June 27 Maths Shift 2 question paper?
No. There is no choice in section A of the JEE Main 2022 June 27 Maths Shift 2 question paper.
Q4
How do you rate the difficulty level of the JEE Main 2022 Maths June 27 Shift 2 question paper out of 3?
We can say that the difficulty level of the JEE Main 2022 Maths June 27 Shift 2 question paper was 1.53 out of 3.
Q5
How many questions are there in section A of the JEE Main 2022 Maths Shift 2 June 27 question paper?
There are 20 questions in section A of the JEE Main 2022 Maths Shift 2 June 27 question paper.


















Comments