The JEE Main 2022 June 24 – Shift 1 Maths Question Paper with Solutions can be viewed on this page. The step-by-step solutions for
JEE Main 2022 Question Papers are prepared by our expert team. Students can also download the JEE Main 2022 June 24 – Shift 1 Maths Question Paper with Solutions in a PDF format for free. They can save these for offline use. JEE Main 2022 answer keys help them to find accurate answers, stepwise. The JEE Main 2022 question papers’ solutions will help students to examine their performance in the JEE Main 2022 exam.
JEE Main 2022 June 24 – Shift 1 Maths Question Paper with Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. Let A = {z ∈ C : 1 ≤ |z – (1 + i)| ≤ 2} and B = {z ∈ A : |z – (1 – i)| = 1}. Then, B :
(A) Is an empty set
(B) Contains exactly two elements
(C) Contains exactly three elements
(D) Is an infinite set
Answer (D)
Sol.
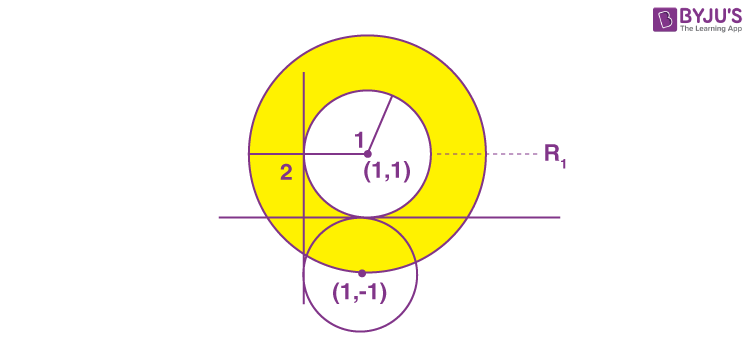
Set A represents region 1 i.e.R1 and clearly set B has infinite points in it.
2. The remainder when 32022 is divided by 5 is :
(A) 1
(B) 2
(C) 3
(D) 4
Answer (D)
Sol. 32022 = (10 – 1)1011
= 1011C0(10)1011 (–1)0 + 1011C1(10)1010 (–1)1 + ….. + 1011C1010(10)1 (–1)1010 + 1011C1011(10)0 (–1)1011
= 5k –1, where k ∈ I
So when divided by 5, it leaves remainder 4.
3. The surface area of a balloon of spherical shape being inflated, increases at a constant rate. If initially, the radius of balloon is 3 units and after 5 seconds, it becomes 7 units, then its radius after 9 seconds is :
(A) 9
(B) 10
(C) 11
(D) 12
Answer (A)
Sol. S = 4πr2
\(\begin{array}{l}\frac{dS}{dt}=8\pi r\frac{dr}{dt}\end{array} \)
\(\begin{array}{l}\frac{dS}{dt}=\text{ constant so} \Rightarrow r\frac{dr}{dt}=k \left ( \text{Let} \right )\end{array} \)
\(\begin{array}{l}r dr=k dt \Rightarrow \frac{r^2}{2}=kt+C\end{array} \)
at t = 0, r = 3
\(\begin{array}{l}\frac{9}{2}=C \end{array} \)
at t = 5,
\(\begin{array}{l}\frac{49}{2}=k\cdot5+\frac{9}{2}\Rightarrow k =4\end{array} \)
At t = 9,
\(\begin{array}{l}\frac{r^2}{2}=\frac{81}{2}\end{array} \)
So, r = 9
4. Bag A contains 2 white, 1 black and 3 red balls and bas B contains 3 black, 2 red and n white balls. One bag is chosen at random and 2 balls drawn from it at random, are found to be 1 red and 1 black. If the probability that both balls come from Bag A is \(\begin{array}{l}\frac{6}{11}\end{array} \)
then n is equal to _______.
(A) 13
(B) 6
(C) 4
(D) 3
Answer (C)
Sol.
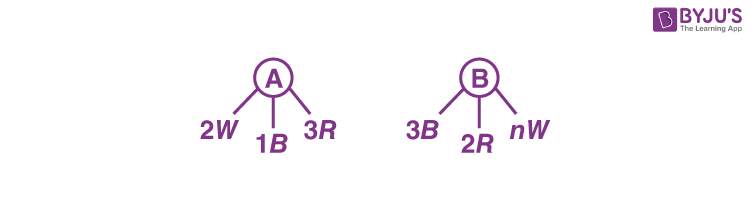
\(\begin{array}{l}P\left ( 1R \text{ and } 1B \right )=P\left ( A \right )\cdot P\left ( \frac{1R 1B}{A} \right )+P\left ( B \right )\cdot P\left ( \frac{1R 1B}{B} \right )\end{array} \)
\(\begin{array}{l}=\frac{1}{2}\cdot\frac{^3C_1\cdot^1C_1}{^6C_2}+\frac{1}{2}\cdot\frac{^2C_1\cdot^3C_1}{^{n+5}C_1}\end{array} \)
\(\begin{array}{l}P\left ( \frac{1R 1B}{A} \right )=\frac{\frac{1}{2}\cdot\frac{3}{15}}{\frac{1}{2}\cdot\frac{3}{15}+\frac{1}{2}\cdot\frac{6\cdot2}{\left ( n+5 \right )\left ( n+4 \right )}}=\frac{6}{11}\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{\frac{1}{10}}{\frac{1}{10}+\frac{6}{(n+5)(n+4)}} =\frac{6}{11}\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{11}{10}=\frac{6}{10}+\frac{36}{(n+5)(n+4)}\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{5}{10 \times 36} =\frac{1}{(n+5)(n+4)}\end{array} \)
⇒ n2 + 9n – 52 = 0
⇒ n = 4 is only possible value
5. Let \(\begin{array}{l}x^2+y^2+Ax+By+C=0\end{array} \)
be a circle passing through (0, 6) and touching the parabola y = x2 at (2, 4). Then A + C is equal to ________.
(A) 16
(B)
\(\begin{array}{l}\frac{88}{5}\end{array} \)
(C) 72
(D) –8
Answer (A)
Sol. For tangent to parabola y = x2 at (2, 4)
\(\begin{array}{l}\left. \frac{dy}{dx} \right|_{(2,4)}=4\end{array} \)
Equation of tangent is
y – 4 = 4(x – 2)
⇒ 4x – y – 4 = 0
Family of circle can be given by
(x – 2)2 + (y – 4)2 + λ(4x – y – 4) = 0
As it passes through (0, 6)
22 + 22 + λ(–10) = 0
\(\begin{array}{l}\Rightarrow \lambda = \frac{4}{5}\end{array} \)
Equation of circle is
\(\begin{array}{l}\left (x-2 \right )^2+\left ( y-4 \right )^2+\frac{4}{5}\left ( 4x-y-4 \right )=0\end{array} \)
\(\begin{array}{l}\Rightarrow \left ( x^2+y^2-4x-8y+20 \right )+\left ( \frac{16}{5}x -\frac{4}{5}y-\frac{16}{5} \right )=0\end{array} \)
\(\begin{array}{l}A=-4+\frac{16}{5},C=20-\frac{16}{5}\end{array} \)
So, A + C = 16
6. The number of values of α for which the system of equations :
x + y + z = α
αx + 2αy + 3z = –1
x + 3αy + 5z = 4
is inconsistent, is
(A) 0
(B) 1
(C) 2
(D) 3
Answer (B)
Sol.
\(\begin{array}{l}\Delta =\begin{vmatrix}1 & 1 & 1 \\\alpha & 2\alpha & 3 \\1 & 3\alpha & 5 \\\end{vmatrix}\end{array} \)
= 1(10α – 9α) – 1 (5α – 3) + 1 (3α2 – 2α)
= α – 5α + 3 + 3α2 – 2α
= 3α2 – 6α + 3
For inconsistency Δ = 0 i.e. α = 1
Now check for α = 1
x + y + z = 1 …(i)
x + 2y + 3z = –1 …(ii)
x + 3y + 5z = 4 …(iii)
By (ii) × 2 – (i) × 1
x + 3y + 5z = –3
so equations are
inconsistent for α = 1
7. If the sum of the squares of the reciprocals of the roots α and β of the equation 3x2 + λx – 1 = 0 is 15, then 6(α3 + β3)2 is equal to :
(A) 18
(B) 24
(C) 36
(D) 96
Answer (B)
Sol.
\(\begin{array}{l}\frac{1}{\alpha^2}+\frac{1}{\beta^2}=15 \Rightarrow \frac{(\alpha+\beta)^2-2\alpha\beta}{\alpha^2\beta^2}=15\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{\frac{\lambda^2}{9}+\frac{2}{3}}{\frac{1}{9}}=15\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{\lambda^2}{9}=1 \Rightarrow \lambda^2=9\end{array} \)
α3 + β3 = (α + β) (α2 + β2 – αβ)
\(\begin{array}{l}=\left ( \frac{-\lambda}{3} \right )\left ( \frac{\lambda^2}{9}-3 \left ( \frac{-1}{3} \right ) \right )=\left(\frac{-\lambda}{3}\right) \left( \frac{\lambda^2}{9}+1 \right )=\frac{-2\lambda}{3}\end{array} \)
\(\begin{array}{l}6\left ( \alpha^3+\beta^3 \right)^2=6\cdot\frac{4\lambda^2}{9}=24\end{array} \)
8. The set of all values of k for which \(\begin{array}{l}\left ( \tan^{-1}x \right )^3+\left ( \cot^{-1}x \right )^3=k\pi ^3, x \in R,\end{array} \)
is the interval:
(A)
\(\begin{array}{l}\left [ \frac{1}{32},\frac{7}{8} \right )\end{array} \)
(B)
\(\begin{array}{l}\left ( \frac{1}{24},\frac{13}{16} \right )\end{array} \)
(C)
\(\begin{array}{l}\left [ \frac{1}{48},\frac{13}{16} \right ]\end{array} \)
(D)
\(\begin{array}{l}\left [ \frac{1}{32},\frac{9}{8} \right )\end{array} \)
Answer (A)
Sol. Let
\(\begin{array}{l}\tan^{-1}x=t\in \left ( \frac{-\pi}{2},\frac{\pi}{2} \right )\end{array} \)
\(\begin{array}{l}\cot^{-1}x=\frac{\pi}{2}-t\end{array} \)
\(\begin{array}{l}f\left ( t \right )=t^3+\left ( \frac{\pi}{2}-t \right )^3 \Rightarrow f’\left ( t \right )=3t^2-3\left ( \frac{\pi}{2}-t\right )^2\end{array} \)
\(\begin{array}{l}f’\left ( t \right )=0 \text{ at } t=\frac{\pi}{4}\end{array} \)
\(\begin{array}{l}f\left ( t\right )\left| \frac{}{}\right._{\min}=\frac{\pi^{3}}{64} + \frac{\pi^{3}}{64}=\frac{\pi^{3}}{32}\end{array} \)
Max will occur around
\(\begin{array}{l}t=-\frac{\pi}{2}\end{array} \)
Range of
\(\begin{array}{l}f(t) =\left[\frac{\pi^3}{32},\frac{7\pi^3}{8} \right )\end{array} \)
\(\begin{array}{l}k \in \left[\frac{1}{32},\frac{7}{8} \right )\end{array} \)
9. Let \(\begin{array}{l}S=\left\{ \sqrt{n}:1\le n \le 50 \text{ and } n \text{ is odd} \right\}\end{array} \)
.
Let
\(\begin{array}{l}a\in S \text{ and } A=\begin{bmatrix}1 & 0 & a \\-1 & 1 & 0 \\-a & 0 & 1 \\\end{bmatrix}\end{array} \)
If
\(\begin{array}{l}\sum_{a~\in~S} \det \left ( adj A \right ) = 100 \lambda\end{array} \)
, then λ is equal to :
(A) 218
(B) 221
(C) 663
(D) 1717
Answer (B)
Sol. |A| = a2 + 1
|adj A| = (a2 + 1)2
\(\begin{array}{l}S=\left\{ 1, \sqrt{3},\sqrt{5},\sqrt{7}, \dots, \sqrt{49} \right\} \end{array} \)
\(\begin{array}{l}\sum_{a~\in~S} \det \left ( adj A \right )=\left ( 1^2 + 1 \right )^2 + \left ( 3 + 1 \right )^2 +\left ( 5 + 1 \right )^2 + \dots + \left ( 49 + 1 \right )^2\end{array} \)
= 22 (12 + 22 + 32 + … + 252)
\(\begin{array}{l}=4\cdot\frac{25\cdot26\cdot51}{6}=100\cdot221\end{array} \)
λ = 221
10. For the function
f(x) = 4 loge(x – 1) – 2x2 + 4x + 5, x > 1, which one of the following is NOT correct?
(A) f is increasing in (1, 2) and decreasing in (2, )
(B) f(x) = –1 has exactly two solutions
(C) f′(e) – f′′(2) < 0
(D) f(x) = 0 has a root in the interval (e, e + 1)
Answer (C)
Sol.
\(\begin{array}{l}f'(x)=\frac{4}{x-1}-4x+4=\frac{4\left ( 2x-x^2 \right )}{x-1}\end{array} \)
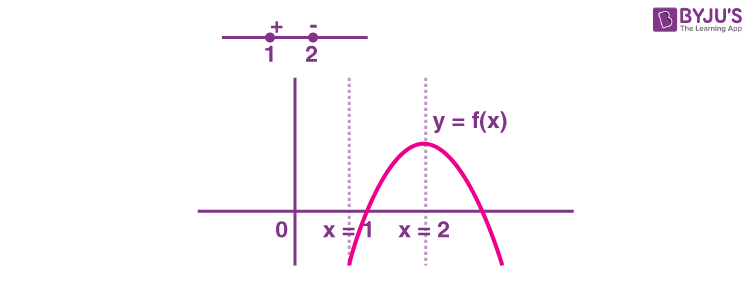
So maxima occurs at x = 2
f(2) = 4⋅0 – 2⋅22 + 4⋅2 + 5 = 5
so clearly f(x) = –1 has
exactly 2 solutions
\(\begin{array}{l}f”(x)=\frac{4(2-2x)(x-1)}{(x-1)^2}-\left( 2x-x^2 \right )\end{array} \)
so f′(e) – f ′′(2) > 0
so option c is not correct
11. If the tangent at the point (x1, y1) on the curve y = x3 + 3x2 + 5 passes through the origin, then (x1, y1) does NOT lie on the curve :
(A)
\(\begin{array}{l}x^2+\frac{y^2}{81}=2\end{array} \)
(B)
\(\begin{array}{l}\frac{y^2}{9}-x^2=8 \end{array} \)
(C) y = 4x2 + 5
(D)
\(\begin{array}{l}\frac{x}{3}-y^2=2\end{array} \)
Answer (D)
Sol.
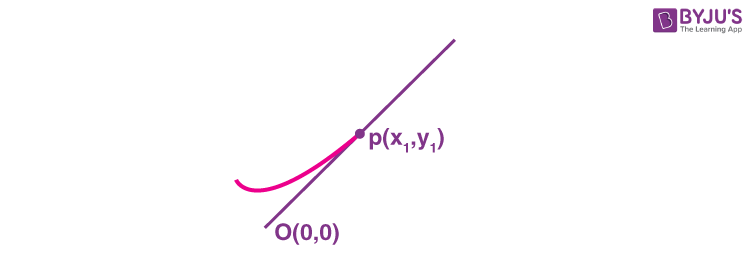
mop – mTangent
\(\begin{array}{l}\frac{y_1}{x_1}=3x_1^2+6x_1\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{x_1^3+3x_1^2+5}{x_1}=3x_1^2+6x_1\end{array} \)
\(\begin{array}{l}\Rightarrow x_1^3+3x_1^2+5=3x_1^3+6x_1^2\end{array} \)
\(\begin{array}{l}\Rightarrow 2x_1^3+3x_1^2-5=0\end{array} \)
\(\begin{array}{l}\Rightarrow \left ( x_1-1 \right )\left ( 2x_1^2+5x_1+5 \right )=0\end{array} \)
So, (x1, y1) = (1, 9)
12. The sum of absolute maximum and absolute minimum values of the function f(x) = |2x2 + 3x – 2| + sinx cosx in the interval [0, 1] is :
(A)
\(\begin{array}{l}3+\frac{\sin(1)\cos^2\left ( \frac{1}{2} \right )}{2} \end{array} \)
(B)
\(\begin{array}{l}3+\frac{1}{2}\left( 1+2\cos(1)\right )\sin(1)\end{array} \)
(C)
\(\begin{array}{l}5+\frac{1}{2}\left ( \sin(1)+sin(2) \right )\end{array} \)
(D)
\(\begin{array}{l}2+\sin\left ( \frac{1}{2} \right )\cos\left ( \frac{1}{2} \right )\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l}f(x)=\left| \left ( 2x-1 \right )\left ( x+2 \right )\right|+\frac{\sin2x}{2}\end{array} \)
\(\begin{array}{l}\underline{0\le x \le \frac{1}{2}}~~~~f(x)=(1-2x)(x+2)+\frac{\sin2x}{2}\end{array} \)
f‘(x) = –4x – 3 + cos2x <0
For
\(\begin{array}{l}x\ge\frac{1}{2}~:~~f'(x)=4x+3+\cos2x>0\end{array} \)
So, minima occurs at
\(\begin{array}{l}x=\frac{1}{2}\end{array} \)
\(\begin{array}{l}f(x)|_{min} = \left| 2\left ( \frac{1}{2} \right )^2 + \frac{3}{2}-2\right|+\sin\left ( \frac{1}{2} \right )\cdot\cos\left ( \frac{1}{2} \right )\end{array} \)
\(\begin{array}{l}=\frac{1}{2}\sin1\end{array} \)
So, maxima is possible at x = 0 or x = 1
Now checking for x = 0 and x = 1, we can see it attains its maximum value at x = 1
\(\begin{array}{l}f(x)|_{max} =\left| 2+3-2\right|+\frac{\sin2}{2}\end{array} \)
\(\begin{array}{l}=3+\frac{1}{2}sin2\end{array} \)
Sum of absolute maximum and minimum value
\(\begin{array}{l}=3+\frac{1}{2}\left(\sin1 + \sin2 \right)\end{array} \)
13. If \(\begin{array}{l}\left\{ a_i\right\}_{i=1}^n\end{array} \)
, where n is an even integer, is an arithmetic progression with common difference 1, and \(\begin{array}{l}\sum_{i=1}^{n}a_i = 192,\sum_{i=1}^{n/2}a_{2i}= 120\end{array} \)
, then n is equal to :
(A) 48
(B) 96
(C) 92
(D) 104
Answer (B)
Sol.
\(\begin{array}{l}a_1+a_2+\ldots+a_n = 192 \Rightarrow\frac{n}{2}\left ( a_1+a_n \right )=192….(1)\end{array} \)
a2 + a4 + a6 + … + an = 120
\(\begin{array}{l}\Rightarrow \frac{n}{4}\left ( a_1+1+a_n \right )=120….(2)\end{array} \)
From (2) & (1)
\(\begin{array}{l}\frac{480}{n}-\frac{384}{n}=1\end{array} \)
⇨ n = 96
14. If x = x(y) is the solution of the differential equation \(\begin{array}{l}y\frac{dx}{dy}=2x+y^3(y+1)e^y, x(1)=0;\end{array} \)
then x(e) is equal to :
(A) e3(ee – 1)
(B) ee(e3 – 1)
(C) e2(ee + 1)
(D) ee(e2 – 1)
Answer (A)
Sol.
\(\begin{array}{l}\frac{dx}{dy}-\frac{2x}{y}=y^2(y+1)e^y\end{array} \)
If
\(\begin{array}{l}=e^{\int-\frac{2}{y}dy}=e^{-2\ln y}=\frac{1}{y^2}\end{array} \)
Solution is given by
\(\begin{array}{l}x\cdot\frac{1}{y^2}=\int y^2\left ( y+1 \right )e^y\cdot\frac{1}{y^2}dy\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{x}{y^2}=\int(y+1)e^ydy\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{x}{y^2}=ye^y + c\end{array} \)
⇒ x = y2 (yey + c)
at, y = 1, x = 0
⇒ 0 = 1(1.e1 + c) ⇒ c = –e
at y = e,
x = e2(e.ee – e)
15. Let λx – 2y = μ be a tangent to the hyperbola a2x2 – y2 = b2. Then \(\begin{array}{l}\left ( \frac{\lambda}{a} \right )^2-\left ( \frac{\mu}{b} \right )^2\end{array} \)
is equal to :
(A) –2
(B) –4
(C) 2
(D) 4
Answer (D)
Sol.
\(\begin{array}{l}\frac{x^2}{\left ( \frac{b^2}{a^2} \right )}-\frac{y^2}{b^2}=1\end{array} \)
Tangent in slope form ⇒
\(\begin{array}{l}y=mx\pm\sqrt{\frac{b^2}{a^2}m^2-b^2}\end{array} \)
i.e., same as
\(\begin{array}{l}y=\frac{\lambda x}{2}-\frac{\mu}{2}\end{array} \)
Comparing coefficients,
\(\begin{array}{l}m=\frac{\lambda}{2}, \frac{b^2}{a^2}m^2-b^2=\frac{\mu^2}{4}\end{array} \)
Eliminating
\(\begin{array}{l}m,\frac{b^2}{a^2}\cdot\frac{\lambda^2}{4}-b^2=\frac{\mu^2}{4}\end{array} \)
\(\begin{array}{l} \Rightarrow\frac{\lambda^2}{a^2}-\frac{\mu^2}{b^2}=4\end{array} \)
16. Let \(\begin{array}{l}\hat{a}, \hat{b}\end{array} \)
be unit vectors. If \(\begin{array}{l}\vec{c}\end{array} \)
be a vector such that the angle between \(\begin{array}{l}\hat{a}\end{array} \)
and \(\begin{array}{l}\vec{c}\end{array} \)
is \(\begin{array}{l}\frac{\pi}{12}\end{array} \)
and \(\begin{array}{l}\hat{b}=\vec{c}+2\left ( \vec {c}\times\hat{a} \right )\end{array} \)
then \(\begin{array}{l}\left|6 \vec{c}\right|^2\end{array} \)
is equal to:
(A)
\(\begin{array}{l}6\left ( 3-\sqrt{3} \right )\end{array} \)
(B)
\(\begin{array}{l}3+\sqrt{3}\end{array} \)
(C)
\(\begin{array}{l}6\left ( 3+\sqrt{3} \right )\end{array} \)
(D)
\(\begin{array}{l}6\left ( \sqrt{3} + 1 \right )\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}\because \hat{b}=\vec{c}+2\left( \vec{c}\times \hat{a} \right )\end{array} \)
\(\begin{array}{l}\Rightarrow \hat{b}\cdot\vec{c}=\left|\vec{c}\right|^2\end{array} \)
…(i)
\(\begin{array}{l}\therefore \hat{b}-\vec{c}=2\left ( \vec{c}\times \vec{a}\right )\end{array} \)
\(\begin{array}{l}\Rightarrow\left|\hat{b}\right|^2 +\left| \vec{c}\right|^2-2\hat{b}\cdot\vec{c}=4\left|\vec{c}\right|^2\left|\vec{a}\right|^2\sin^2\frac{\pi}{12}\end{array} \)
\(\begin{array}{l} \Rightarrow 1+\left| \vec{c}\right|^2-2\left| \vec{c}\right|^2 =4\left| \vec{c}\right|^2\left ( \frac{\sqrt{3}-1}{2\sqrt{2}} \right )^2\end{array} \)
\(\begin{array}{l}\Rightarrow 1=\left| \vec{c}\right|^2\left ( 3-\sqrt{3} \right )\end{array} \)
\(\begin{array}{l}\Rightarrow 36\left| \vec{c}\right|^2=\frac{36}{3-\sqrt{3}}=6\left ( 3+\sqrt{3} \right )\end{array} \)
17. If a random variable X follows the Binomial distribution B(33, p) such that 3P(X = 0) = P(X = 1), then the value of \(\begin{array}{l}\frac{P\left ( X=15 \right )}{P\left ( X=18 \right )}-\frac{P\left ( X=16 \right )}{P\left ( X=17 \right )}\end{array} \)
is equal to:
(A) 1320
(B) 1088
(C)
\(\begin{array}{l}\frac{120}{1331}\end{array} \)
(D)
\(\begin{array}{l}\frac{1088}{1089}\end{array} \)
Answer (A)
Sol. 3P(X = 0) = P(X = 1)
\(\begin{array}{l}3\cdot^nC_0P^0\left ( 1-P \right )^n=~^nC_1P^1\left ( 1-P \right )^{n-1}\end{array} \)
\(\begin{array}{l}\frac{3}{n}=\frac{P}{1-P}\Rightarrow \frac{1}{11}=\frac{P}{1-P}\end{array} \)
⇒ 1 – P = 11P
\(\begin{array}{l}\Rightarrow P=\frac{1}{12}\end{array} \)
\(\begin{array}{l}\frac{P(X=15)}{P(X=18)}-\frac{P(X=16)}{P(X=17)}\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{^{33}C_{15}P^{15}(1-P)^{18}}{^{33}C_{18}P^{18}(1-P)^{15}}-\frac{^{33}C_{16}P^{16}(1-P)^{17}}{^{33}C_{17}P^{17}(1-P)^{16}}\end{array} \)
\(\begin{array}{l}\Rightarrow \left ( \frac{1-P}{P} \right )^3-\left ( \frac{1-P}{P} \right )\end{array} \)
⇒ 113 – 11 = 1320
18. The domain of the function \(\begin{array}{l}f(x)=\frac{\cos^{-1}\left ( \frac{x^2-5x+6}{x^2-9} \right )}{\log_e\left ( x^2-3x+2 \right )}\end{array} \)
is:
(A)
\(\begin{array}{l}\left ( -\infty,1 \right )\cup\left ( 2, \infty \right )\end{array} \)
(B) (2, ∞)
(C)
\(\begin{array}{l}\left [ -\frac{1}{2},1 \right )\cup\left ( 2,\infty \right )\end{array} \)
(D)
\(\begin{array}{l}\left [ -\frac{1}{2},1 \right )\cup\left ( 2,\infty \right )-\left\{ \frac{3+\sqrt{5}}{2},\frac{3-\sqrt{5}}{2}\right\}\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l}-1\le \frac{x^2-5x+6}{x^2-9}\le 1\end{array} \)
and x2 – 3x + 2 > 0, ≠ 1
\(\begin{array}{l}\frac{\left ( x-3 \right )\left ( 2x+1 \right )}{x^2-9}\ge 0 \left|\frac{5(x-3)}{x^2-9} \right.\ge 0\end{array} \)
Solution to this inequality is
\(\begin{array}{l}x\in \left [ \frac{-1}{2},\infty \right )-\{3\}\end{array} \)
for x2 – 3x + 2 > 0 and ≠ 1
\(\begin{array}{l}x\in\left ( -\infty,1 \right )\cup \left ( 2,\infty \right )-\left\{ \frac{3-\sqrt{5}}{2},\frac{3+\sqrt{5}}{2}\right\}\end{array} \)
Combining the two solution sets (taking intersection)
\(\begin{array}{l}x\in \left [ \frac{-1}{2},1 \right )\cup\left ( 2,\infty \right )-\left\{ \frac{3-\sqrt{5}}{2},\frac{3+\sqrt{5}}{2}\right\}\end{array} \)
19. Let \(\begin{array}{l}S=\left\{ \theta \in \left [ -\pi, \pi \right ]-\left\{ \pm\frac{\pi}{2}\right\}: \sin\theta\tan\theta + \tan\theta=\sin2\theta\right\}\end{array} \)
. If \(\begin{array}{l}T=\sum_{\theta = S}\cos2\theta\end{array} \)
then T + n(S) is equal to:
(A)
\(\begin{array}{l}7+\sqrt{3}\end{array} \)
(B) 9
(C)
\(\begin{array}{l}8+\sqrt{3}\end{array} \)
(D) 10
Answer (B)
Sol. tanθ (sinθ + 1) – sin2θ = 0
tanθ (sinθ + 1 – 2cos2θ) = 0
⇒ tanθ = 0 or 2sin2θ + sinθ – 1 = 0
⇒ (2sinθ + 1)(sinθ – 1) = 0
⇒
\(\begin{array}{l}\sin\theta=\frac{-1}{2}\end{array} \)
or 1
But, sinθ = 1 not possible
\(\begin{array}{l}\theta = 0, \pi, – \pi, -\frac{\pi}{6},\frac{-5\pi}{6}\end{array} \)
n(S) = 5
\(\begin{array}{l}T=\sum\cos2\theta=cos0^\circ + \cos2\pi + \cos(-2\pi)+\cos\left ( -\frac{5\pi}{3} \right )+\cos\left ( -\frac{\pi}{3} \right )\end{array} \)
= 4
20. The number of choices for \(\begin{array}{l}\Delta \in \left\{ \land, \lor, \Rightarrow, \Leftrightarrow \right\}\end{array} \)
such that (p Δ q) ⇒ ((p Δ ~ q) ∨ ((~p) Δ q)) is a tautology, is
(A) 1
(B) 2
(C) 3
(D) 4
Answer (B)
Sol. Let x : (pΔq) ⇒ (pΔ ~ q) ∨ (~pΔq)
Case-I
When Δ is same as ∨
Then (pΔ~q) ∨ (~pΔq) becomes
(p ∨ ~q) ∨ ( ~p ∨ q) which is always true, so x becomes a tautology.
Case-II
When Δ is same as ∧
Then (p ∧ q) ⇒ (p ∧ ~q) ∨ (~p ∧ q)
If p ∧ q is T, then (p ∧ ~ q) ∨ (~ p ∧ q) is F
so x cannot be a tautology.
Case-III
When Δ is same as ⇒
Then (p ⇒ ~ q) ∨ (~ p ⇒ q) is same at (~ p ∨ ~ q) ∨ (p ∨ q), which is always true, so x becomes a tautology.
Case-IV
When Δ is same as ⇔
Then (p ⇔ q) ⇒ (p ⇔ ~ q) ∨ (~ p ⇔ q)
p ⇔ q is true when p and q have same truth values, then p ⇔ ~ q and ~p ⇔ q both are false. Hence x cannot be a tautology.
So finally x can be ∨ or ⇒.
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, –00.33, –00.30, 30.27, –27.30) using the mouse andw the on-screen virtual numeric keypad in the place designated to enter the answer.
1. The number of one-one functions ƒ : {a, b, c, d} → {0, 1, 2, …, 10} such that 2ƒ(a) – ƒ(b) + 3ƒ(c) + ƒ(d) = 0 is ________.
Answer (31)
Sol. 3ƒ(c) + 2ƒ(a) + ƒ(d) = ƒ(b)
|
Value of ƒ(c)
|
Value of ƒ(a)
|
Number of functions
|
|
0
|
1
|
7
|
|
2
|
5
|
|
3
|
3
|
|
4
|
2
|
|
1
|
0
|
6
|
|
2
|
2
|
|
3
|
1
|
|
2
|
0
|
3
|
|
1
|
1
|
|
3
|
0
|
1
|
|
Total Number of functions =
|
31
|
2. In an examination, there are 5 multiple choice questions with 3 choices, out of which exactly one is correct. There are 3 marks for each correct answer, –2 marks for each wrong answer and 0 mark if the question is not attempted. Then, the number of ways a student appearing in the examination gets 5 marks is _____.
Answer (40)
Sol. Let student marks x correct answers and y incorrect. So
3x – 2y = 5 and x + y 5 where x, y W
Only possible solution is (x, y) = (3, 2)
Student can mark correct answer by only one choice but for incorrect answer, there are two choices. So total number of ways of scoring 5 marks = 5C3(1)3. (2)2 = 40
3. Let \(\begin{array}{l}A\left ( \frac{3}{\sqrt{a}},\sqrt{a} \right ), a > 0\end{array} \)
, be a fixed point in the xy-plane, The image of A in y-axis be B and the image of B in x-axis be C. If D(3cosθ, asinθ) is a point in the fourth quadrant such that the maximum area of ΔACD is 12 square units, then a is equal to ______.
Answer (8)
Sol. Clearly B is
\(\begin{array}{l}\left ( -\frac{3}{\sqrt{a}},+\sqrt{a} \right )\end{array} \)
and C is \(\begin{array}{l}\left ( -\frac{3}{\sqrt{a}},-\sqrt{a} \right )\end{array} \)
Area of
\(\begin{array}{l}\Delta ACD =\frac{1}{2}\begin{vmatrix}\frac{3}{\sqrt{a}} & \sqrt{a} & 1 \\-\frac{3}{\sqrt{a}} & -\sqrt{a} & 1 \\3\cos\theta & a\sin\theta & 1 \\\end{vmatrix}\end{array} \)
⇒
\(\begin{array}{l}\Delta =\begin{vmatrix}0 & 0 & 1 \\-\frac{3}{\sqrt{a}} & -\sqrt{a} & 1 \\3\cos\theta & a\sin\theta & 1 \\\end{vmatrix}\end{array} \)
\(\begin{array}{l}\Rightarrow \Delta = \left| 3\sqrt{a}\sin\theta +3\sqrt{a}\cos\theta\right|=3\sqrt{a}\left|\sin\theta + \cos\theta \right|\end{array} \)
\(\begin{array}{l}\Rightarrow \Delta_{\max} = 3\sqrt{a}\cdot\sqrt{2}=12 \Rightarrow a = \left ( 2\sqrt{2} \right )^2=8\end{array} \)
4. Let a line having direction ratios 1, –4, 2 intersect the lines \(\begin{array}{l}\frac{x-7}{3}=\frac{y-1}{-1}=\frac{z+2}{1}\end{array} \)
and \(\begin{array}{l}\frac{x}{2}=\frac{y-7}{3}=\frac{z}{1}\end{array} \)
at the points A and B. Then (AB)2 is equal to _________.
Answer (84)
Sol. Let A(3λ + 7, –λ + 1, λ – 2) and B (2μ, 3μ + 7, μ)
So, DR’s of AB ∝ 3λ – 2μ + 7, – (λ + 3μ + 6), λ – μ – 2
Clearly
\(\begin{array}{l}\frac{3\lambda-2\mu+7}{1}=\frac{\lambda+3\mu+6}{4}=\frac{\lambda-\mu-2}{2}\end{array} \)
⇒ 5λ – 3μ = –16 …(i)
And λ – 5μ = 10 …(ii)
From (i) and (ii) we get λ = –5, μ = –3
So, A is (–8, 6, –7) and B is (–6, –2, –3)
\(\begin{array}{l}AB=\sqrt{4+64+16}\Rightarrow \left ( AB \right )^2=84\end{array} \)
5. The number of points where the function
\(\begin{array}{l}f(x)=\begin{cases}\left| 2x^2-3x-7\right| & \text{if } x\le-1 \\\left [ 4x^2-1 \right ] &\text{if }-1<x<1 \\\left| x+1\right| + \left| x-2\right| & \text{if } x \ge 1 \\\end{cases} \end{array} \)
[t] denotes the greatest integer ≤ t, is discontinuous is _____________.
Answer (7)
Sol. f (–1) = 2 and f (1) = 3
For x ∈ (–1, 1), (4x2 – 1) ∈ [–1, 3)
hence f(x) will be discontinuous at x = 1 and also
whenever 4x2 – 1 = 0, 1 or 2
\(\begin{array}{l}\Rightarrow x=\pm\frac{1}{2}, \pm\frac{1}{\sqrt{2}} \text{ and }\pm\frac{\sqrt{3}}{2}\end{array} \)
So there are total 7 points of discontinuity.
6. Let \(\begin{array}{l}f(\theta)=sin\theta + \int_{-\pi/2}^{\pi/2}\left ( \sin\theta + t\cos\theta \right )f(t)dt\end{array} \)
. Then the value of \(\begin{array}{l}\left|\int_{0}^{\pi/2}f(\theta)d\theta \right|\end{array} \)
is _________.
Answer (1)
Sol.
\(\begin{array}{l}f(\theta) = \sin\theta\left ( 1+ \int_{-\pi/2}^{\pi/2}f(t)dt\right )+cos\theta\left (\int_{-\pi/2}^{\pi/2}tf(t)dt\right)\end{array} \)
Clearly f(θ) = asinθ + bcosθ
Where
\(\begin{array}{l}a=1+\int_{-\pi/2}^{\pi/2}\left ( a\sin t + b\cos t \right )dt \Rightarrow a= 1+ 2b ~~~~~\dots (1)\end{array} \)
and
7. Let \(\begin{array}{l}\underset{0 \le x \le 2}{\text{Max}}\left\{ \frac{9-x^2}{5-x}\right\}=\alpha \end{array} \)
and \(\begin{array}{l}\underset{0 \le x \le 2}{\text{Min}}\left\{ \frac{9-x^2}{5-x}\right\}=\beta\end{array} \)
.
If
\(\begin{array}{l}\int_{\beta-\frac{8}{3}}^{2\alpha -1} \text{Max}\left\{ \frac{9-x^2}{5-x},x\right\}dx =\alpha_1 + \alpha_2 \log_e\left ( \frac{8}{15} \right )\end{array} \)
then \(\begin{array}{l}\alpha_1 + \alpha_2\end{array} \)
is equal to __________.
Answer (34)
Sol. Let
\(\begin{array}{l}f(x)=\frac{x^2-9}{x-5}\Rightarrow f'(x)=\frac{(x-1)(x-9)}{(x-5)^2}\end{array} \)
So, α = f(1) = 2 and
\(\begin{array}{l}\beta = \min\left ( f(0), f(2) \right )= \frac{5}{3}\end{array} \)
Now,
\(\begin{array}{l}\int_{-1}^{3}\max \left\{ \frac{x^2-9}{x-5}, x\right\}dx = \int_{-1}^{9/5}\frac{x^2-9}{x-5}dx+\int_{9/5}^{3}x~dx\end{array} \)
\(\begin{array}{l}=\int_{-1}^{9/5}\left ( x+5+\frac{16}{x-5} \right )dx + \frac{x^2}{2}\left. \frac{}{} \right|_{9/5}^3\end{array} \)
\(\begin{array}{l}=\frac{28}{25}+14+16 \ln\left ( \frac{8}{15} \right )+\frac{72}{25}=18+16\ln\left ( \frac{8}{15} \right )\end{array} \)
Clearly
\(\begin{array}{l}\alpha_1 = 18\end{array} \)
and \(\begin{array}{l}\alpha_2 = 16\end{array} \)
, so \(\begin{array}{l}\alpha_1 + \alpha_2 = 34\end{array} \)
8. If two tangents drawn from a point (α, β) lying on the ellipse 25x2 + 4y2 = 1 to the parabola
y2 = 4x are such that the slope of one tangent is four times the other, then the value of (10α + 5)2 + (16β2 + 50)2 equals ____________.
Answer (2929)
Sol. ∵ (α, β) lies on the given ellipse, 25α2 + 4β2 = 1
…(1)
Tangent to the parabola,
\(\begin{array}{l}y=mx+\frac{1}{m}\end{array} \)
passes through (α, β). So, αm2 – βm + 1 = 0 has roots m1 and 4m1,
\(\begin{array}{l}m_1+4m_1=\frac{\beta}{\alpha}\end{array} \)
and \(\begin{array}{l}m_1\cdot4m_1=\frac{1}{\alpha}\end{array} \)
Gives that 4β2 = 25α …(2)
from (1) and (2)
25(α2 + α) = 1 …(3)
Now, (10α + 5)2 + (16β2 + 50)2
= 25(2α + 1)2 + 2500 (2α + 1)2
= 2525 (4α 2 + 4α + 1) from equation (3)
\(\begin{array}{l}=2525\left ( \frac{4}{25}+1 \right )\end{array} \)
= 2929
9. Let S be the region bounded by the curves y = x3 and y2 = x. The curve y = 2|x| divides S into two regions of areas R1 and R2.strong>
If max {R1, R2} = R2, then
\(\begin{array}{l}\frac{R_2}{R_1}\end{array} \)
is equal to _____.
Answer (19)
Sol.
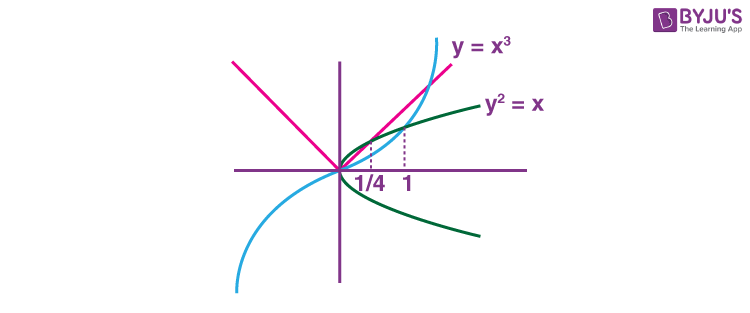
C1 : y = x3
C2 : y2 = x
and C3 = y = 2|x|
C1 and C2 intersect at (1, 1)
C2 and C3 intersect at
\(\begin{array}{l}\left ( \frac{1}{4}, \frac{1}{2} \right )\end{array} \)
Clearly
\(\begin{array}{l}R_1 = \int_{0}^{1/4}\left ( \sqrt{x}-2x \right )dx = \frac{2}{3}\left ( \frac{1}{8} \right )-\frac{1}{16}=\frac{1}{48}\end{array} \)
and
\(\begin{array}{l}R_1 +R_2 = \int_{0}^{1}\left ( \sqrt{x}-x^3 \right )dx = \frac{2}{3}-\frac{1}{4}=\frac{5}{12}\end{array} \)
So,
\(\begin{array}{l}\frac{R_1+R_2}{R_1}=\frac{5/12}{1/48}\Rightarrow1 + \frac{R_2}{R_1}=20\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{R_2}{R_1}=19\end{array} \)
10. If the shortest distance between the lines \(\begin{array}{l}\vec{r}=\left ( -\hat{i}+3\hat{k} \right )+\lambda\left ( \hat{i}-a\hat{j} \right )\end{array} \)
and \(\begin{array}{l}\vec{r}=\left ( -\hat{j}+2\hat{k} \right )+\mu\left ( \hat{i}- \hat{j}+\hat{k} \right )\end{array} \)
is \(\begin{array}{l}\sqrt{\frac{2}{3}}\end{array} \)
, then the integral value of a is equal to ______________.
Answer (2)
Sol.
\(\begin{array}{l}\vec{b_1}\times\vec{b_2}=\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\1 & -a & 0 \\1 & -1 & 1 \\ & & \\\end{vmatrix} =-a\hat{i}-\hat{j}+(a-1)\hat{k}\end{array} \)
\(\begin{array}{l}\vec{a_1}-\vec{a_2}=-\hat{i} + \hat{j}+\hat{k}\end{array} \)
Shortest distance
\(\begin{array}{l}=\left| \frac{(\vec{a_1}-\vec{a_2})\cdot(\vec{b_1}\times\vec{b_2})}{\left| \vec{b_1}\times\vec{b_2}\right|}\right|\end{array} \)
\(\begin{array}{l}\Rightarrow \sqrt{\frac{2}{3}}=\frac{2(a-1)}{\sqrt{a^2+1+(a-1)^2}}\end{array} \)
\(\begin{array}{l}\Rightarrow 6\left ( a^2-2a+1 \right )=2a^2-2a+2\end{array} \)
\(\begin{array}{l}\Rightarrow (a-2)(2a-1)=0 \Rightarrow a = 2 \text{ because } a \in z\end{array} \)
.
❑ ❑ ❑
Download PDF Here

















Very nice
Jee notes
Get JEE Main notes here.
https://byjus.com/jee/jee-main-notes/
JEE main previous questions and answers
Get JEE Main previous year papers here.
https://byjus.com/jee/jee-main-question-paper/