JEE Main 2020 solved shift 2 Physics paper consists of step by step solutions, prepared by our subject specialists. Practising these solutions will help students to get an idea of what type of questions are asked from each chapter. These solutions are given in a way such that students can easily understand the problems. These solutions can be easily downloaded from our website in PDF format for free.
JEE Main 2020 Question Papers
January 7 Shift 2 – Physics
Download PDF 
January 7 Shift 2 – Physics
1. A box weighs 196 N on a spring balance at the North Pole. Its weight recorded on the same balance if it is shifted to the equator is close to (Take g = 10m/s2 at the North Pole and radius of the Earth = 6400 km )
a. 194.32 N
b. 194.66 N
c. 195.32 N
d. 195.66 N
Weight of the object at the pole,W = mg = 196 N
Mass of the object, m = w/g = 196/10 = 19.6 kg
Weight of object at the equator (W’) = Weight at pole – Centrifugal acceleration
W’ = 196 – 19.6(2π/24×3600)2×6400×103 = 195.33 N
Answer: (c)
2. In a building, there are 15 bulbs of 45 W, 15 bulbs of 100 W, 15 small fans of and 2 heaters of 1kW. The voltage of electric main is 220V. The minimum fuse capacity (rated value) of the building will be approximately
a. 10 A
b. 20 A
c. 25 A
d. 15 A
Total power consumption of the house (P) = Number of appliances ×Power rating of each appliance
P = (15×45) + (15×100) + (15×10)+(2×1000) = 4325 W
So, minimum fuse current, I = Total power consumption/Voltage supply
= 4325/220
= 19.66 A
Answer: (b)
3. Under an adiabatic process, the volume of an ideal gas gets doubled. Consequently, the mean collision time between the gas molecules changes from τ1 to τ2. If Cp/Cv = γ for this gas, then a good estimate for τ2 /τ1 is given by
a. 1/2
b. (1/2) (γ +1)/2
c. (1/2) γ
d. 2
Relaxation time (τ) dependence on volume and temperature can be given by τ ∝ V/√T.
Also for an adiabatic process,
T ∝
\(\begin{array}{l}\frac{1}{V^{\gamma -1}}\end{array} \)
τ ∝ V (1+γ)/2
τ 2/ τ 1 = (V/2V) (1+γ)/2
τ 2/ τ 1 = (1/2) (1+γ)/2
Answer: (b)
4. A mass of 10 kg is suspended by a rope of length 4 m, from the ceiling. A force F is applied horizontally at the mid-point of the rope such that the top half of the rope makes an angle of 45° with the vertical. Then F equals (Take g = 10 m/s2 and rope to be massless)
a. 100 N
b. 90 N
c. 75 N
d. 70 N
Equating the vertical and horizontal components of the forces acting at point

T/√2 = 100
T/√2 = F
F = 100 N
Answer: (a)
5. Mass per unit area of a circular disc of radius a depends on the distance r from its centre as σ(r) = A + Br. The moment of inertia of the disc about the axis, perpendicular to the plane and passing through its centre is
a. \(\begin{array}{l}2\pi a^{4}(\frac{A}{4}+\frac{aB}{5})\end{array} \)
b. \(\begin{array}{l}2\pi a^{4}(\frac{aA}{4}+\frac{B}{5})\end{array} \)
c. \(\begin{array}{l}\pi a^{4}(\frac{A}{4}+\frac{aB}{5})\end{array} \)
d. \(\begin{array}{l}2\pi a^{4}(\frac{A}{4}+\frac{B}{5})\end{array} \)
= A + Br
∫dm = ∫(A+Br) 2πrdr
I = ∫dm r2
= ∫0a(A+Br)2πr3dr
= 2 π(A (a4/4) + B(a5/5))
= 2π a4 (A/4) + Ba/5)
Answer: (a)
6. Two ideal Carnot engines operate in cascade (all heat given up by one engine is used by the other engine to produce work) between temperatures T1 and T2. The temperature of the hot reservoir of the first engine is T1 and the temperature of the cold reservoir of the second engine is T2. T is the temperature of the sink of first engine which is also the source for the second engine. How is T related to T1 and T2 if both the engines perform equal amount of work?
a. T = 2T1T2/(T1+T2)
b. T = (T1+T2)/2
c. T = 0
d. T = √T1T2
Heat input to 1st engine = QH
Heat rejected from 1st engine= Q
Heat rejected from 2nd engine= QL
Work done by 1st engine = Work done by 2nd engine
QH – Q = Q – QL
2Q = QH + QL
2 = (T1 + T2)/T
T = (T1 + T2)/2
Answer: (b)
7. The activity of a radioactive substance falls from 700 s-1 to 500 s-1 in 30 minutes. Its half life is close to
a. 66 min
b. 62 min
c. 52 min
d. 72 min
Using the half-life equation
ln A0/At = λt
At half life, t = λt1/2 and At = A0/2
ln 2 = λt1/2 …..(i)
Also given
ln(700/500) = λ×30 … (ii)
Dividing the equations ln 2/ ln (7/5) = t1/2 /30
t1/2 = 61.8 minutes.
Answer: (b)
8. In a Young’s double slit experiment, the separation between the slits is 0.15 mm. In the experiment, a source of light of wavelength 589 nm is used and the interference pattern is observed on a screen kept 1.5 m away. The separation between the successive bright fringes on the screen is
a. 5.9 mm
b. 3.9 mm
c. 6.9 mm
d. 4.9 mm
β= λD/d
= 589 ×10-9 × 1.5/(0.15 x 10-3)
= 5.9 mm
Answer: (a)
9. An ideal fluid flows (laminar flow) through a pipe of non-uniform diameter. The maximum and minimum diameters of the pipes are 6.4 cm and 4.8 cm, respectively. The ratio of minimum and maximum velocities of fluid in this pipe is
a. √(3/2)
b. 9/16
c. 3/4
d. √3/4
Given,
Maximum diameter of pipe = 6.4
Minimum diameter of pipe = 4.8
Using equation of continuity A1V1 = A2V2
V1/V2 = A2/A1
= (4.8/6.4)2
= 9/16
Answer: (b)
10. In the figure, potential difference between a and b is
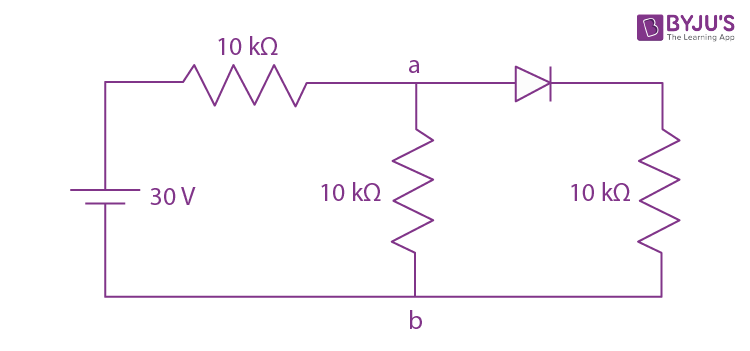
a. 0 V
b. 15 V
c. 10 V
d. 5 V
Diode is in forward bias, so it will behave as simple wire. So, the circuit effectively becomes

Vab = (30×5)/(5+10)
= (30×5)/15
= 10 V
Answer: (c)
11. A particle of mass m and charge q has an initial velocity \(\begin{array}{l}\vec{v} = v_{0}\: \hat{j}\end{array} \)
. If an electric field \(\begin{array}{l}\vec{E} = E_{0}\: \hat{i}\end{array} \)
and magnetic field \(\begin{array}{l}\vec{B} = B_{0}\: \hat{i}\end{array} \)
act on the particle, its speed will double after a time
a. √3mv0/qE0
b. √2mv0/qE0
c. 3mv0/qE0
d. 2mv0/qE0
Magnetic field can only change direction of speed as it cannot do any work.
As
\(\begin{array}{l}\vec{v} = v_{0}\: \hat{j}\end{array} \)
(magnitude of velocity does not change in y–z plane)
(2V0)2 = (V0)2 + (Vx )2
Vx = √3 V0
√3 V0 = 0 + qE0t/m
t = √3 mV0 /qE0
Answer: (a)
12. A stationary observer receives sound from two identical tuning forks, one of which approaches and the other one receded with the same speed (much less than the speed of sound). The observer hears 2 beats/sec. The oscillation frequency of each tuning fork is v0 = 1400 Hz and the velocity of sound in air is 350 m/s. The speed of each tuning fork is close to
a. 1/4 m/s
b. 1 m/s
c. 1/2 m/s
d. 1/8 m/s
f0 C/(C-V)- f0C/(C+V)= 2
V = ¼ m/s
Answer: (a)
13. An electron (of mass m) and a photon have the same energy E in the range of few eV. The ratio of the de Broglie wavelength associated with the electron and the wavelength of the photon is. ( c = speed of light in vacuum)
a. (E/2m)1/2
b. 1/c (2E/m)1/2
c. c(2mE)1/2
d. 1/c (E/2m)1/2
λd for electron = h/√(2me)
λp for photon = hc/E
Ratio = [h/√(2me) ] E/hc
= (1/c)√(E/2m)
Answer: (d)
14. A planar loop of wire rotates in a uniform magnetic field. Initially at t = 0, the plane of the loop is perpendicular to the magnetic field. If it rotates with a period of 10 s about an axis in its plane, then the magnitude of induced emf will be maximum and minimum, respectively at
a. 2.5 sec and 5 sec
b. 5 sec and 7.5 sec
c. 2.5 sec and 7.5 sec
d. 5 sec and 10 sec
ω = 2π/T = π/5
when ωt = π/2
Then φflux will be minimum.
e will be maximum.
t = (π/2)/(π/5) = 2.5 sec
When ωt =π
Then φflux will be maximum
e will be minimum.
t = π/(π/5) = 5 sec
Answer: (a)
15. The electric field of a plane electromagnetic wave is given by \(\begin{array}{l}\vec{E}(t) = E_{0}\frac{(\hat{i}+\hat{j})}{\sqrt{2}}\cos (kz+\omega t)\end{array} \)
At t = 0, a positively charged particle is at the point (x,y,z) = (0,0,/k ). If its instantaneous velocity at t = 0 is v0
\(\begin{array}{l}\hat{k}\end{array} \)
, the force acting on it due to the wave is
a. zero
b. antiparallel to \(\begin{array}{l}\frac{\hat{i}+\hat{j}}{\sqrt{2}}\end{array} \)
c. parallel to \(\begin{array}{l}\frac{\hat{i}+\hat{j}}{\sqrt{2}}\end{array} \)
d. parallel to \(\begin{array}{l}\hat{k}\end{array} \)
Force due to electric field is in direction
\(\begin{array}{l}\frac{-(\hat{i}+\hat{j})}{\sqrt{2}}\end{array} \)
Because at t = 0, E =
\(\begin{array}{l}\frac{-(\hat{i}+\hat{j})}{\sqrt{2}}E_{0}\end{array} \)
Force due to magnetic field is in direction
\(\begin{array}{l}q(\vec{v}\times \vec{B})\end{array} \)
and v ǁk
It is parallel to
\(\begin{array}{l}\vec{E}\end{array} \)
Net force is antiparallel to
\(\begin{array}{l}\frac{\hat{i}+\hat{j}}{\sqrt{2}}\end{array} \)
Answer: (b)
16. A thin lens made of glass (refractive index 1.5) of focal length f = 16 cm is immersed in a liquid of refractive index 1.42. If its focal length in liquid is fi, then the ratio fl/ f is closest to the integer
a. 9
b. 17
c. 1
d. 5
\(\begin{array}{l}\frac{1}{f_{a}} = \left ( \frac{\mu _{g}}{\mu _{a}} -1\right )\left ( \frac{1}{R_{1}}-\frac{1}{R_{2}} \right )\end{array} \)
\(\begin{array}{l}\frac{1}{f_{1}} = \left ( \frac{\mu _{g}}{\mu _{m}} -1\right )\left ( \frac{1}{R_{1}}-\frac{1}{R_{2}} \right )\end{array} \)
\(\begin{array}{l}\frac{f_{a}}{f_{1}} =\frac{\left ( \frac{\mu _{g}}{\mu _{1}} -1\right )}{\left ( \frac{\mu _{g}}{\mu _{a}} -1\right )}\end{array} \)
=
\(\begin{array}{l}\frac{\frac{1.50}{1.42}-1}{\frac{1.50}{1}-1} = \frac{0.08}{1.42\times 0.5}\end{array} \)
f1/fa = 1.42×0.5/0.08 = 8.875 = 9
Answer: (a)
17. An elevator in a building can carry a maximum of 10 persons, with the average mass of each person being 68 kg. The mass of the elevator itself is 920 kg and it moves with a constant speed of 3 m/s. The frictional force opposing the motion is 6000N. If the elevator is moving up with its full capacity, the power delivered by the motor to the elevator (g = 10 m/s2) must be atleast
a. 66000 W
b. 63360 W
c. 48000 W
d. 56300 W
Net force on motor will be
Fm = (920 + 68(10)]10 + 6000
= 22000 N
So, required power for motor
\(\begin{array}{l}P_{m}= \vec{F_{m}}. \vec{v}\end{array} \)
= 22000 × 3
= 66000 W
Answer: (a)
18. The figure gives experimentally measured B vs H variation in a ferromagnetic material. The retentivity, coercivity and saturation, respectively, of the material are
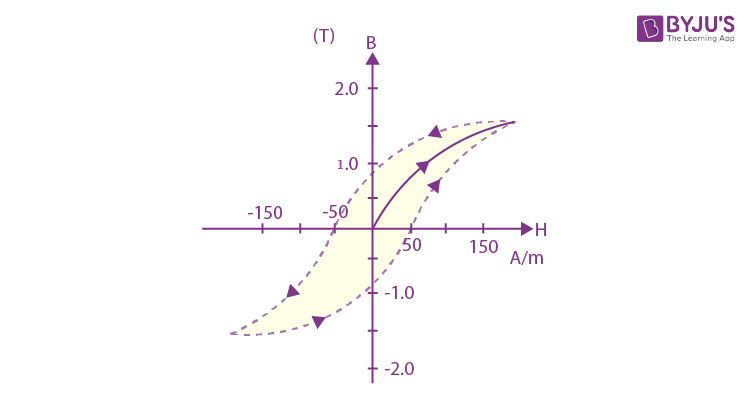
a. 1.5 T, 50 A/m, 1 T
b. 1 T, 50 A/m, 1.5 T
c. 1.5 T, 50 A/m, 1 T
d. 150 A/m, 1 T, 1.5 T

x = retentivity
y = coercivity
z = saturation magnetization
Answer: (b)
19. An emf of 20 V is applied at time t = 0 to a circuit containing in series 10 mH inductor and 5 Ω resistor. The ratio of the currents at time t = ∞ and t = 40 s is close to take e2= 7.389)
a. 1.06
b. 1.46
c. 1.15
d. 0.84
i = i0( 1- e-t/L/R)
= (20/5)( 1-e-t/0.01/5)
= 4(1-e-500t)
i∞ = 4
i40 = 4(1 – e-500×40)
= 4( 1- 1/(e2)1000)
= 4( 1 – 1/7.38910000)
i∞ /i40 ≈ 1 (Slightly greater than one)
Answer: (a)
20. The dimension of B2/2μ0 where B is magnetic field and μ0 is the magnetic permeability of vacuum, is
a. ML-1T-2
b. ML2T-2
c. MLT-2
d. ML2T-1
Energy density in magnetic field = B2/2 μ0
= force ×displacement/(displacement)3
= MLT-2. L/L3
= ML-1T-2
Answer: (a)
21. A 60 pF capacitor is fully charged by a 20 V supply. It is then disconnected from the supply and is connected to another uncharged 60 pF capacitor in parallel. The electrostatic energy that is lost in this process by the time the charge is redistributed between them is __(in nJ)


V0 = 20 V
Initial potential energy Ui = ½ CV02
After connecting identical capacitor in parallel, voltage across each capacitor will be V0/2. Then, final potential energy Uf = 2 [ ½ C(V0/2)2]
Heat loss = Ui – Uf
= (CV02/2) – (CV02/4) = CV02/4
= (60 ×10-12×202/4)
= 6×10-9
= 6 nJ
Answer: (6)
22. M grams of steam at 1000C is mixed with 200g of ice at its melting point in a thermally insulated container. If it produces liquid water at 400 C[heat of vaporization of water is 540 cal/g and heat of fusion of ice is 80 cal/g ], the value of M is __.
Here, heat absorbed by ice = mice Lf + mice Cw(40-0)
Heat released by steam = msteam Lv + msteam Cw(100-40)
Heat absorbed = heat released
mice Lf + mice Cw(40-0) = msteam Lv + msteam Cw(100-40)
200×80 cal/g + 200×1 cal/g/0C ×(40 – 0)
= m ×540 cal/g + 540×1 cal/g/0C ×(100 – 40)
200[80 + 40] = m[540+ 60]
M = 40g
Answer:(40)
23. Consider a uniform cubical box of side a on a rough floor that is to be moved by applying minimum possible force F at a point above its centre of mass (see figure). If the coefficient of friction is μ = 0.4, the maximum value of 100 ×b/a for the box not to topple before moving is __.

F balances kinetic friction so that the block can move
So, F = μmg
For no toppling, the net torque about bottom right edge should be zero.
F((a/2) + b) ≤ mg a/2
μmg((a/2) + b) ≤ mg a/2
μ(a/2) + μb ≤ a/2
0.2a + 0.4b ≤ 0.5a
0.4b ≤ 0.3a
b ≤ ¾ a
But, maximum value of b can only be 0.5a.
Maximum value of 100(b/a) is 50.
Answer: (50)
24. The sum of two forces \(\begin{array}{l}\vec{P}\end{array} \)
and \(\begin{array}{l}\vec{Q}\end{array} \)
is \(\begin{array}{l}\vec{R}\end{array} \)
such that \(\begin{array}{l}\vec{R}\end{array} \)
= |P|\(\begin{array}{l}\left | \vec{R} \right | = \left | \vec{P} \right |\end{array} \)
. The angle θ (in degrees) that the resultant of \(\begin{array}{l}\vec{2P}\end{array} \)
and \(\begin{array}{l}\vec{Q}\end{array} \)
will make with \(\begin{array}{l}\vec{Q}\end{array} \)
is __

Answer: (90°)
25. The balancing length for a cell is 560 cm in a potentiometer experiment. When an external resistance of 10 Ω is connected in parallel to the cell, the balancing length changes by 60 cm. If the internal resistance of the cell is N/10 Ω, the value of N is
Let the emf of cell is Ɛ internal resistance is r and potential gradient is x.
Ɛ = 560 x …(i)
After connecting the resistor
Ɛ×10/(10+r) = 500 x … (ii)
From (i) and (ii)
560×10/(10+r) = 500 s
56 = 50 + 5r
r = 6/5
= 1.2 Ω
n = 12


Answer.(12)
Video Lessons – January 7 Shift 2 Physics















Comments